Attractive vortices

Ernst Helmut Brandt; Shi-Ping  Zhou

Viewpoint

Attractive vortices

Ernst Helmut Brandt

Max-Planck-Institut für Metallforschung, Heisenbergstr. 3, D-70506 Stuttgart, Germany

Shi-Ping Zhou

Department of Physics, 99 Shangda Road, Shanghai University,Shanghai 200444, China

March 16, 2009• Physics 2, 22

Decoration experiments of the two-gap superconductor

{MgB}_{2}

show evidence for long-range attraction between vortices in a superconducting mixed state, which is interpreted as coexisting type-I and type-II superconductivity.

Figure caption — **Figure 1:** Schematic of the spatial distribution of the superconducting order parameter $| ψ (x) |$ and the field profile $B (x)$ for two neighboring fluxons in (top) type-I, (middle) type-II, and (bottom) type-1.5 superconductors. The bottom sketch in each panel shows $| ψ (x) |$ in a color plot with darker regions indicating the smaller order parameter, and the stray field emanating from the sample surface.

Superconductors are usually categorized as being either type-I or type-II, depending on their behavior under a magnetic field. Now, researchers at Katholieke Universiteit Leuven report in Physical Review Letters that they have found evidence for a superconducting phase that spans these categories, showing coexisting type-I and type-II behavior .

The fascinating phenomenon of superconductivity was discovered in 1911 in Leiden by Heike Kamerlingh-Onnes when he observed that mercury completely loses its electrical resistivity when cooled down to the temperature of liquid helium, 4.2 K. In 1913 he was awarded the Nobel Prize in Physics for his discovery. However, it would take almost 50 years until the superconducting state was explained by the microscopic theory of John Bardeen, Leon Neil Cooper, and Robert Schrieffer (BCS theory, Nobel Prize 1972) as being due to the formation of electron pairs that can move through the crystal without being scattered by the atoms.

Long before BCS theory, however, some very successful phenomenological theories of superconductors had been conceived: in 1935 Fritz and Heinz London introduced the London depth $λ$ , the distance to which an applied magnetic field can penetrate the surface of a superconductor, and in 1953 Brian Pippard introduced the Pippard length $ξ_{P}$ . The most powerful tool, however, is the Ginzburg-Landau (GL) theory, conceived in 1950 by Lev Landau and Vitali Ginzburg. They introduced a similar penetration depth $λ$ as London, over which the magnetic field can vary spatially, and a similar coherence length $ξ$ as Pippard, over which the complex GL function $ψ$ can vary. Both $λ (T)$ and $ξ (T)$ diverge when the temperature $T$ approaches the transition temperature $T_{c}$ , but their ratio $κ = λ / ξ$ , is a constant material parameter called the GL parameter . These three phenomenological theories can be derived from the BCS theory in particular cases. This was shown by Lev Gor’kov in 1959, who derived the GL theory for the case $T \approx T_{c}$ .

In their original publication of 1950, Ginzburg and Landau showed that the solutions of their GL equations behave quite differently when $κ < 1 / \sqrt{2} = 0.71$ or $κ > 0.71$ . In particular, the interface wall energy between a normal conducting (normal state) region and a superconducting (Meissner state) region is positive when $κ < 0.71$ and negative when $κ > 0.71$ . This property distinguishes what have come to be called type-I and type-II superconductors. A type-I superconductor ( $κ < 0.71$ ) under a magnetic field smaller than the thermodynamical critical field $H_{c}$ expels the magnetic field from its interior. For applied fields larger than the critical field, the sample is in the normal state, fully penetrated by the magnetic field. Because of demagnetization effects that are always present for real samples, the effective applied field is enhanced by a demagnetization field. By contrast, in normal magnets a similar field reduces the effective applied field. For fields between $(1 - N) H_{c}$ , where $N$ is the demagnetization factor given by the geometry of the sample and $H_{c}$ , this demagnetization field leads to the appearance of an intermediate state, in which regions of both normal and Meissner state coexist. While across the superconductor, the overall ratio of the normal and Meissner state areas can be calculated easily, the size and detailed shape of the domains and their mushrooming and splitting near the surface are difficult to calculate .

For type-II superconductors with $κ > 0.71$ , the negative wall energy means that the superconductor wants to split into as many domains as possible, even for samples that show no demagnetization effects. In other words, it is unstable. Alexei Abrikosov, a student of Landau, showed in 1957 how nature solves this problem . Abrikosov discovered a periodic solution of the GL equations and interpreted it as the presence, for $κ > 0.71$ , of a lattice of vortices in the supercurrent, each vortex (also called a flux line or fluxon) carrying one quantum of magnetic flux $Φ_{0} = h / 2 e = 2.07 \cdot 10^{- 15} {Tm}^{2}$ . In 2003, Abrikosov and Ginzburg received the Nobel Prize for their theories, together with Anthony Leggett.

The Abrikosov vortices repel each other, often forming a triangular lattice. At low inductions their magnetic repulsion of range $λ$ (that can also be derived from London theory) is partly compensated by an attraction that has a range of $ξ / \sqrt{2}$ , that comes from the overlap of the vortex cores . Vortex cores are the regions where the order parameter $ψ$ goes to zero over a length $\approx ξ$ , the core radius. At $κ = 1 / \sqrt{2}$ these two parts of the interaction exactly cancel, i.e., the vortices do not interact. At smaller $κ < 0.71$ , the vortices should attract, but from GL theory it also follows that the penetration of Abrikosov vortices is not energetically favorable in this case.

Interestingly, the type-I and type-II distinction has been known to be more complex for some time. For pure niobium, which has a GL parameter $κ$ very close to 0.71 depending on its purity, any small deviation from the GL theory might lead to the attraction of vortices. Indeed, at $T < T_{c}$ , decoration experiments on the surface of pure niobium platelets observed magnetic patterns that look like the various patterns observed in type-I superconductors, but now consisting of Meissner state and vortex state, e.g., islands with vortex lattice surrounded by Meissner state, or vice versa, see Ref. and Fig. 4 in Ref. . This observation can be explained by the appearance of a long-range vortex attraction that causes an S-shape (unstable) magnetization curve from which the equilibrium states are obtained by a Maxwell construction, see Fig. 3 of Ref. .

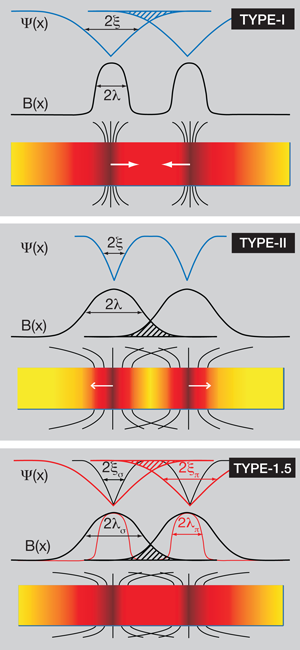
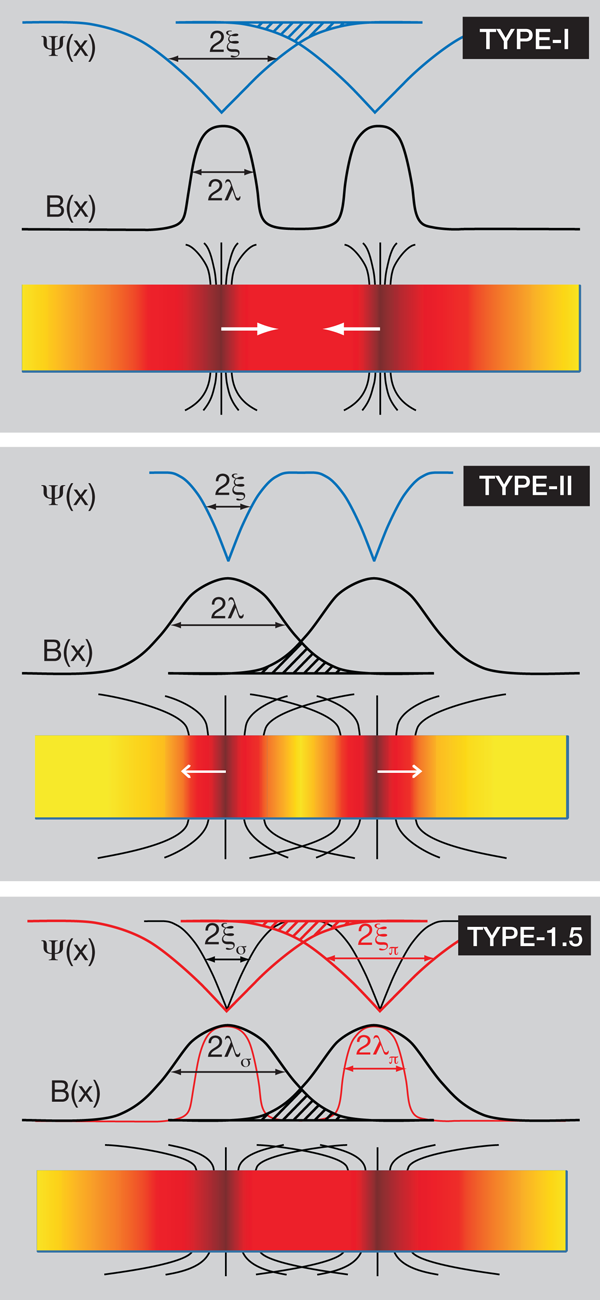
Victor Moshchalkov et al. argue that in the recently discovered two-band superconductor ${MgB}_{2}$ , the presence of two nearly independent order parameters $ψ_{π}$ and $ψ_{σ}$ , corresponding to the two electronic bands that carry the superconductivity, may lead to novel effects related to the attraction of vortices. They showed that from the two-band GL functional follows a vortex–vortex interaction that is short-range repulsive and weakly long-range attractive, as was also found by Babaev . Particularly fascinating effects should occur when the GL parameters of the $π$ and $σ$ bands, and of the two corresponding superfluids, are $κ_{π} = λ_{π} / ξ_{π} = 0.66 < 0.71$ and $κ_{σ} = λ_{σ} / ξ_{σ} = 3.68 > 0.71$ , as they find from measured energy gaps, Fermi velocities, and plasma frequencies. ${MgB}_{2}$ should thus have properties of both type-I and type-II superconductors simultaneously. The authors of Ref. name this type-1.5 superconductivity. Figure 1 shows the suggested spatial profiles of $ψ$ and $B$ for vortices in type-I, II, and 1.5 superconductors; for the latter they suggest the existence of two different core widths, corresponding to the $π$ and $σ$ components, as it is expected for complete absence of interband coupling.

The predicted vortex attraction and potential minimum should occur in a wide range of materials parameters, in contrast to the very particular case of $κ \approx 1 / \sqrt{2}$ mentioned above. This minimum stabilizes unconventional stripe- and gossamer-like vortex patterns, as observed also in magnetic films, colloids, polymers, gels, etc., see Ref. for a short review.

To check their prediction of type 1.5 behavior, Moshchalkov et al. show images of vortex arrangements obtained by decoration experiments on field-cooled ${MgB}_{2}$ and, for comparison, ${NbSe}_{2}$ , and of computer simulations at very low inductions. Field cooling means that the distance of the potential minimum, $r_{0} \propto (1 - T / T_{c})^{- 1 / 2}$ , decreases from $r_{0} = \infty$ at $T = T_{c}$ when the vortices nucleate, to a value several times $λ (0)$ . For ${MgB}_{2}$ , Fig. 2(a) (experiment at $H = 1$ Oe) and Fig. 2(b) (simulation) in Ref. show chains of nearly equidistant vortices, and Fig. 3(a) and Fig. 3(c) show condensation of vortices into clusters. All these features are absent in the corresponding images for ${NbSe}_{2}$ and thus indicate that in ${MgB}_{2}$ , vortices indeed have a potential with attractive tail and minimum.

In conclusion, the ideas and results of Ref. are highly interesting and will certainly stimulate further investigation into the fascinating field of two-component superconductivity. One should advance the theories and the measurement of their input parameters, and account for the coupling terms in their solution. One should investigate the singlet-triplet mixtures of pairing states near a halfmetal–superconductor interface, and a two-band BCS-type Hamiltonian to capture the essential features in hole-doped iron-based superconductors . Note that during the decoration experiments in Ref. the applied field is much less than the vortex penetration field $(1 - N) H_{c 1}$ , where $H_{c 1}$ is the lower critical field, and the vortices would thus mostly leave the specimen if they were not pinned. The main challenge will be finding experimental ways to separate the effects of pinning and vortex attraction.

References

V. Moshchalkov, M. Menghini, T. Nishio, Q. H. Chen, A. V. Silhanek, V. H. Dao, L. F. Chibotaru, N. D. Zhigadlo, and J. Karpinski, Phys. Rev. Lett.PRLTAO10.1103/PhysRevLett.102.117001 102, 117001 (2009)
P. G. DeGennes, Superconductivity of Metals and Alloys (Benjamin, New York, 1966) 0201408422
M. Tinkham, Introduction to Superconductivity (McGraw-Hill, New York, 1975)0070648778
L. D. Landau and E. M. Lifshits, Electrodynamics of Continuous Media (Pergamon, New York , 1960)0750626348
A. Hubert, Phys. Stat. Sol. 24, 669 (1967)10.1002/pssb.19670240229
A. A. Abrikosov, Zh. Exp. Teor. Fiz. 32, 1442, (1957) [Sov. Phys. JETP 5, 1174, (1957)]
E. H. Brandt, Phys. Rev. B 10.1103/PhysRevB.34.651434, 6514 (1986)
U. Essmann and H. Träuble, Sci. Am. 224,75 (1971)
E. H. Brandt, Rep. Prog. Phys. 10.1088/0034-4885/58/11/00358, 1465 (1995)
E. Babaev and M. Speight, Phys. Rev. B 72, 180502 (2005)10.1103/PhysRevB.72.180502
C. J. Olson Reichhardt, C. Reichhardt, I. Martin, and A. R. Bishop, Physica D 10.1016/j.physd.2004.01.027193, 303 (2004)
A. Gurevich, Physica C 10.1016/j.physc.2007.01.008456, 160 (2007)
F. Hunte , Nature 10.1038/nature07058453, 903 (2008)

About the Authors

Ernst Helmut Brandt is a physicist in the Max Planck Institute for Metals Research in Stuttgart, Germany. Helmut’s theoretical work has always been concerned with the Abrikosov vortex lattice in type-II superconductors, particularly with the ideal lattice, its nonlocal elastic response, lattice defects, pinning, and effects of geometry on the electromagnetic response of superconductors. He received his diploma and Ph.D. from Stuttgart University and has been for extended visits at Moscow University, Ames Laboratory, AT&T Bell Laboratories, and Shanghai University. He was named an Outstanding Referee by the American Physical Society in 2008.

Shi-Ping Zhou received his Ph.D. degree in physics from Shanghai University of Science and Technology, Shanghai, China, in 1989. He continued his research at Liverpool University in England (1992–1994), at Hamburg-Harburg University in Germany (1997–1999), and at CNRS in Grenoble, France (1999). Currently, Shi-ping Zhou is professor at the Department of Physics at Shanghai University. His research interests include microscopic theory of the vortex lattice in cuprate superconductors, nonequilibrium transport in confined quantum systems, and interaction between magnetism and superconductivity.