A little entanglement helps

Ulrich Schollwöck

Viewpoint

A little entanglement helps

Physics Department and Arnold Sommerfeld Center for Theoretical Physics, Ludwig-Maximilians-Universität München, D-80333 München, Germany

May 11, 2009• Physics 2, 39

A new algorithm allows for the extremely efficient calculation of thermally averaged quantities in one dimension, in conjunction with the density matrix renormalization group method. The key is the judicious selection of a few representative states.

Figure caption — **Figure 1:** The algorithm begins with a classical state. Minimally entangled typical thermal states (METTS) are created by evolving a classical state in imaginary time. Subsequently, by performing a quantum measurement on the METTS, a new classical state is created and the circle closes. After discarding the first few METTS produced from this loop in order to erase any memory of the initial choice, an ensemble of only a few states allows calculation of static quantities (such as energy or magnetization) with high accuracy.

Over the past decades, the numerical simulation of quantum many-body systems has evolved into a major field of condensed matter physics. Strongly interacting Hamiltonians on lattices, such as the Hubbard and Heisenberg models, are of particular interest as they are relevant for a variety of physical systems, including low-dimensional magnets, high- $T_{c}$ superconductors, and ultracold atomic gases in optical lattices. Writing in Physical Review Letters [1], Steve White at the University of California, Irvine, provides, at least in one dimension, a new algorithm (see Fig. 1) that for a given quantum system allows for a highly efficient calculation of static quantities (e.g., energy or magnetization of a chain of spins) at arbitrary finite temperature and holds promise for dynamical quantities. The underlying theme of this success is the peculiar behavior of entanglement in many-body systems.

Why are simulations of strongly interacting Hamiltonians difficult? The principal challenge is that the number of states needed to describe a quantum system increases exponentially with its size. For $N$ classical two-valued spins versus $N$ quantum spins of $1 / 2$ , a point in state space is characterized by $2 N$ versus $2^{N}$ variables. Numerical methods have to adapt to this exponential growth: exact diagonalization techniques analyze the full state space, while Monte Carlo techniques explore it stochastically. But does one have to work with the entirety of the Hilbert space? A wealth of other techniques try to find and work with much smaller, hopefully physically relevant, subspaces. Examples include all renormalization group and variational techniques, and among them is the density matrix renormalization group (DMRG) pioneered by White [2,3] in 1992.

DMRG is an already highly successful method that currently generates a lot of excitement because it is profoundly connected to quantum information theory through the idea of entanglement. Expanding on this well-established connection to ground states at zero temperature, White shows that one can use entanglement even at finite temperature, where it is understood poorly, to design a highly efficient simulation method based on DMRG.

DMRG is a method which, for a given Hamiltonian, variationally optimizes over a particular set of states—the so-called matrix product states (MPS). These are states where the scalar coefficients of the wave function expansion are derived from a product of $D \times D$ dimensional matrices, depending only on local lattice site states. $D$ is the key control parameter, determining both accuracy and computation time: compared to the exponential number of wave-function coefficients for the full Hilbert space, there is only a polynomial number of parameters in an MPS. Verstraete and Cirac [4] recently proved that MPS approximate ground-state physics of generic local Hamiltonians in one dimension, even for small $D$ , to almost exponential accuracy—an observation that had intrigued practitioners of DMRG for a long time. In ground-state physics, therefore, the enormously large Hilbert space is, in some sense, only an illusion.

The nice feature exploited by White is that the efficiency of MPS and DMRG can be motivated (if we abandon rigor and focus on “physically” realistic Hamiltonians) by the existence of area laws for quantum mechanical entanglement in ground states. Let us partition a lattice into parts A and B, and measure pure state entanglement as the von Neumann entropy of part A, $S = - Tr ρ_{A} {log}_{2} ρ_{A}$ with the reduced density operator defined as $ρ_{A} = {Tr}_{B} | ψ 〉 〈 ψ |$ by explicit summation over the states in part B. $S$ will be extensive for a random state from Hilbert space (e.g., it will depend on the number of lattice sites comprising part A). However, ground states turn out to be highly atypical: for gapped systems, entanglement scales merely as the surface of A (e.g., in one dimension it is a single lattice site), with possible logarithmic corrections at criticality.

For a MPS, reduced density operators have dimension $D$ , and the maximum entanglement the state can carry is $S = {log}_{2} D$ . Conversely, we will need at least $D = 2^{S}$ as the dimension of a MPS that is an accurate description of a state with entanglement $S$ . DMRG therefore succeeds or fails depending on the amount of entanglement present! In one dimension, where $S$ is roughly a constant in the system size $L$ (or logarithmic at criticality), $D$ does not grow substantially, i.e., at most polynomially with $L$ . In two dimensions, for systems of size $L^{2}$ , $S \propto L$ entails exponential growth of $D$ , and DMRG fails, at least for larger systems.

At finite temperature, however, the special nature of ground states will not help in DMRG, and therefore it seems a natural expectation that setting up a DMRG procedure would be a real challenge, if not impossible. But the apparent complexity of the thermal density operator $e^{- β H} = Σ_{i} e^{- E_{i}} | E_{i} 〉 〈 E_{i} |$ as an ensemble of exponentially many pure states is again, in some sense, only an illusion! Indeed, we can interpret any mixed state of some physical system A as the reduced density operator $ρ_{A}$ for some pure state $| ψ 〉$ living on system AB, where B is just a copy of system A: a mixed state on a spin chain corresponds to a pure state on a spin ladder. This trick has been used recently for thermal mixed states $e^{- β H}$ to develop a finite-temperature DMRG algorithm. One starts with a pure state with maximal entanglement between A and B (e.g., a spin singlet on each bond for the spin ladder) [5], which leads to a maximally mixed state on A, i.e., the infinite temperature $(β = 0)$ density operator. This state is then subjected to an imaginary time evolution using time-dependent DMRG [6] to the desired temperature $β$ .

This works well, but as White points out, one can avoid purification entirely. This is particularly relevant at low temperatures, where the mixed state of A evolves towards the pure ground state. But then A is not entangled with B anymore, and DMRG simulates a product of two pure states. That amounts to describing a ground state with $D^{2}$ states where only $D$ would have been enough. As a result, low-temperature simulations, where most relevant quantum effects occur, become overly costly.

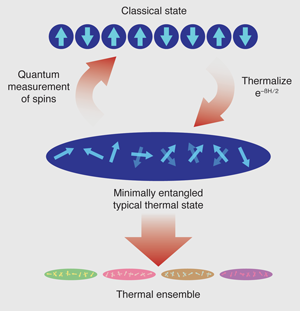
What White proposes instead is to move away from the focus on the energy representation of $ρ$ —as already pointed out by Schrödinger many decades ago, although mathematically correct, such a representation is unphysical since real systems at finite temperature will usually not be in energy eigenstates. Equilibration would be exponentially slow, and eigenstates are highly fragile. White rather exploits unitary freedom in the representation of $ρ$ and introduces “typical” states by doing imaginary time evolutions on any complete orthonormal set of states and constructing $ρ$ from those. The intriguing part of White’s work is that he considers a special set of such typical states: as his initial set he simply takes the “classical” product states, which have no entanglement. Subsequently, the imaginary time evolution introduces entanglement due to the action of the Hamiltonian, but it is a reasonable expectation that the final entanglement will be lower than for similar evolutions of already entangled states. Hence he calls the typical states he obtains “minimally entangled typical thermal states” (METTS). The computational cost is low: dimensions will not blow up as in the purification approach, and low entanglement means that the DMRG computing cost will be low.

Still, this would not be useful if it had to be done for all classical product states. However, White formulates the procedure by analogy to the updates in Monte Carlo steps: the last METTS is used to produce the next classical state (and from there the next METTS) by a quantum measurement of all spins in the current METTS (see Fig. 1). It turns out that–after discarding the first few METTS to eliminate effects of the initial choice–averaging quantities over only a hundred or so states allows calculation of local static quantities (magnetizations, bond energies) with high accuracy and extremely low computational cost compared to previous approaches. This is surprising and exciting.

Intriguing questions concerning both the potential and the foundation of the algorithm remain. How well will it perform for correlation functions? Dynamical quantities can be accessed easily, as the time-evolution of the weakly entangled METTS is not costly, but will the efficiency of averaging over only a few “typical” states continue to hold? This relates to the fundamental question: Why are so few METTS sufficient? My conjecture is that the choice of classical initial states is not only convenient for entanglement reasons, they also have large variance in energy and overlap with many eigenstates, such that sequences of imaginary time evolution and quantum measurement should mimic a thermalized ensemble very quickly (the most inefficient approach would be to start from the eigenstates themselves). In any case, we seem to get a tantalizing hint that for physical manifestations, only small parts of the Hilbert space really matter, and that we can find them systematically.

References

S. R. White, Phys. Rev. Lett. 102, 190601 (2009)
S. R. White, Phys. Rev. Lett. 69, 2863 (1992)
U. Schollwöck, Rev. Mod. Phys. 77, 259 (2005)
F. Verstraete and J. I. Cirac, Phys. Rev. B 73, 094423 (2006)
F. Verstraete, J. J. García-Ripoll, and J. I. Cirac, Phys. Rev. Lett. 93, 207204 (2004); G. Vidal, 91, 147902 (2003)
S. R. White and A. E. Feiguin, Phys. Rev. Lett. 93, 076401 (2004); A. J. Daley, C. Kollath, U. Schollwöck, and G. Vidal, J. Stat. Mech.: Theor. Exp. P04005 (2004)

About the Author

Ulrich Schollwöck is a professor of theoretical physics at the Ludwig-Maximilians-Universität, Munich, Germany. He studied physics in Munich and Oxford, and received his Ph.D. in 1995 at the Service de Physique Theorique of the French Atomic Energy Commission (CEA), Saclay. He was a professor of physics at RWTH Aachen University from 2004 to 2009. His major interests in research are strongly correlated quantum systems in low dimensions and computational condensed matter physics. He is a fellow of the American Physical Society.