Straightening messy correlations with a quantum comb

Matthias  Christandl

Viewpoint

Straightening messy correlations with a quantum comb

Matthias Christandl

Faculty of Physics, Ludwig-Maximilians-Universität München, Munich, Germany

November 23, 2009• Physics 2, 99

Complex systems of entangled quantum states can now be transformed into a simpler form.

Figure caption — **Figure 1:** (Top left) Many-particle systems exhibit complex, messy entanglement structures. (Top right) Entanglement combing straightens out the correlations among the parties so that ebits are created between Alice and each of the Bobs individually. A curly line on the right stands for one ebit, hence $n_{1} = 3$ , $n_{2} = 1$ , $n_{3} = 2$ , and $n_{4} = 1$ in this example. (Bottom left) The initial entangled state of Alice, Bob, and Charlie is $| ψ 〉_{A B C}$ . If $S (B | A) \leq 0$ , then Bob can transfer (or merge) his state to Alice by sending classical messages only. (Bottom right) In addition to the successful transfer, Alice and Bob will share $- S (B | A)$ ebits at the end of the protocol; in the displayed example we have $- S (B | A) = 2$ .

When we don’t pay attention to our hair during the night, it becomes messy and we need to straighten it out in the morning. Particles in quantum physics seem like that—when we don’t pay attention to them, they interact in unintended ways and build up a messy correlation structure known as entanglement. Entanglement is studied in quantum information theory. Here, the information stored in a particle is divided into basic units, called qubits. When two qubits are entangled in the strongest possible way, they form an “entangled bit” or “ebit” that can be used in quantum cryptography or quantum teleportation (in which the quantum state of one system is transferred to a distant system). When entanglement appears in a messy form, however, it is responsible for undesired effects such as decoherence. In a paper appearing in Physical Review Letters [1], Dong Yang at Jiliang University, China, and Jens Eisert (both also at the University of Potsdam, Germany) propose “entanglement combing,” a new technique to convert the messy entanglement of many particles into ebits. Besides new protocols for quantum communication, entanglement combing provides us with a fresh view on the little-understood entanglement structure of many particles.

In recent years, researchers have gained a thorough understanding of the entanglement of two particles. In particular, they have studied how the entanglement of two particles—one given to Alice and one given to Bob, who is far away from Alice—can be transformed into ebits, that is, into states of the form

Here, $| 0 〉$ and $| 1 〉$ stand for orthogonal states of one qubit (for instance spin up and spin down of a spin- $1 / 2$ particle). The case of many particles distributed to many distant parties has remained largely untouched, however, since the number of different ways in which particles can be entangled increases rapidly with the number of particles.

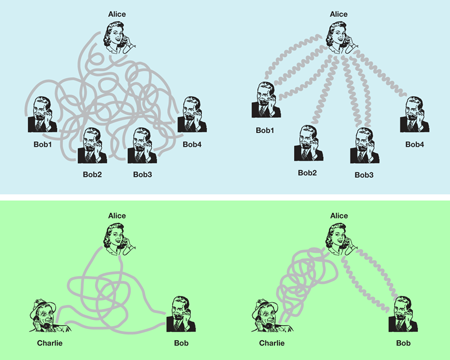
The paper by Yang and Eisert proposes a new technique for the conversion of messy entanglement of many particles into ebits. The ebits resulting from the protocol connect one special party, Alice ( $A$ ), with all the others, which I will call Bob 1 to Bob $m$ ( $B_{1}$ to $B_{m}$ ). The top panels of Fig. 1 illustrate the initial and final correlation structures, which give the protocol the name “entanglement combing.” Quantum communication, for instance the communication with single photons through a glass fiber, is a costly resource, so all transformations are being carried out with classical communication only, for instance over a conventional telephone line. The protocol is, furthermore, carefully constructed so as to result in the optimal number of ebits.

Entanglement combing builds upon two recent highlights in the understanding of entanglement transformations: “state merging” [2] and “entanglement of assistance” [3] (see the bottom panels of Fig. 1). These are best explained with a situation involving three parties, Alice, Bob, and Charlie, who each possess one of three particles that are in an entangled state $| ψ 〉_{A B C}$ . “State merging” is a protocol that allows for the transfer of the state of Bob’s particle to Alice without affecting the correlations with Charlie. The protocol involves sending classical messages between Alice and Bob and requires Alice and Bob to share an additional number of ebits. The number of ebits needed equals the uncertainty that Alice has about the state of Bob’s particle. This uncertainty is measured in terms of the conditional von Neumann entropy $S (B | A)$ of the state of Alice and Bob’s particle, a quantity that generalizes the Shannon entropy of a random variable [4]. In contrast to classical information theory, entanglement can make $S (B | A)$ negative, in which case ebits are gained and not consumed. In “entanglement of assistance,” Charlie helps Alice and Bob to convert their state into ebits by measuring his own system and communicating his result. In this way, Alice and Bob can obtain a number of ebits that equals the minimum of the local entropies $S (A)$ and $S (B)$ .

Iterating these two protocols many times in a clever way, Yang and Eisert are able to convert the messy entanglement between Alice and the many Bobs given in terms of the state $| ψ 〉_{A B_{1} . . . B_{m}}$ into a number of ebits, $n_{i}$ , between Alice and the $i$ th Bob, that is, into $| ϕ 〉_{A B_{1}}^{\otimes n_{1}} \otimes$ … $\otimes | ϕ 〉_{A B_{m}}^{\otimes n_{m}}$ (see Fig. 1). The basic idea is to merge, one by one, the states of the Bobs to Alice, thereby generating the desired ebits. It is important to note that this only works if one actually gains ebits in state merging [i.e., if $S (B_{i} | A) \leq 0$ ] and not if entanglement is consumed [ $S (B_{i} | A) > 0$ ]. Therefore, if Bob $i$ is in the latter situation he does not merge his state to Alice, but instead he assists his neighbor Bob $i + 1$ and Alice in obtaining ebits. Following this procedure until each Bob has either merged his state to Alice or helped his neighbor to create ebits with Alice will lead to the desired result. Interestingly, this protocol results in the highest number of ebits that Alice can share with other parties and is thus optimal. Note that one may choose a different order in which to merge the Bobs to Alice or let them assist.

In quantum communication, the standard way to distribute entanglement is via glass fibers connecting the different parties. Since quantum communication is noisy in general, however, the resulting states are noisy pairs of qubits described by a mixed density matrix rather than ebits. From the noisy qubit pairs one may distill ebits using a variety of entanglement distillation protocols [5]. Entanglement combing does not apply to this situation because the starting state must be a pure state of the particles. An alternative way of distributing ebits, however, is as follows. Envision a messenger who, before going on his daily route, has entangled a bunch of particles by letting them interact. He then distributes the particles one by one to Alice and the Bobs who would like to use their entanglement in a later quantum communication protocol. Since the messenger does not have the interaction under perfect control, however, the resulting state is not in the form of ebits, but instead has a messy entanglement structure of the form $| ψ 〉_{A B_{1} . . . B_{m}}$ .

Entanglement combing provides a way to convert this state into a set of ebits between Alice and the Bobs. They can now be used in a variety of ways in quantum communication theory. Imagine, for instance, a world-wide web connecting quantum computers of users (the Bobs) to a powerful quantum search engine at Alice’s place. Then the Bobs may use the ebits in order to teleport [6] their query (in the form of a quantum state) to Alice who in turn processes it and teleports the (quantum) answers back to the individual Bobs. Alternatively, we may use the ebits for other communication tasks such as quantum cryptography [7] or superdense coding, a method to double the classical communication capacity [8].

A further application of Yang and Eisert’s work is to many-body physics, for instance in condensed matter physics. Through interactions, a set of particles produces a complicated entanglement structure that is responsible for both phase transitions [9] and decoherence [10]. Often, we will not be able to separate the particles as the messenger had done in the way described above, and as a consequence, we will not be able to transform the entanglement using local operations and classical communication. Nevertheless, the authors’ work provides a new tool to advance the understanding of complicated entanglement structures. If, for instance, we would like to compare two many-particle states, we can proceed as follows: In a first step we compute the combed form of the states and in a second step we compare these forms. In this way we can draw conclusions regarding the relation between the two entangled states. This technique may thus be regarded as a novel way of comparing the correlations in different materials, and hence comparing the materials themselves.

How to classify the entanglement in a multiparty system has long been an open question. Although a complete solution to this problem is still out of reach, entanglement combing provides a significant step forward towards a solution of this problem. Further work in this direction may prove to be useful in solving this fundamental physical problem completely.

Acknowledgments

I thank Mario Berta, Roger Colbeck, and Henriette Steiner for comments on the manuscript and acknowledge financial support by the Excellence Network of Bavaria (TMP, QCCC) and the DFG grants CH 843/1-1 and CH 843/2-1

References

D. Yang and J. Eisert, Phys. Rev. Lett. 103, 220501 (2009)
M. Horodecki, J. Oppenheim, and A. Winter, Nature 436, 673 (2005)
J. A. Smolin, F. Verstraete, and A. Winter, Phys. Rev. A 72, 1 (2005)
Mathematically, S(B|A) = S(AB) - S(A), where S(A) and S(AB) are the von Neumann entropies of the reduced density operators of Alice’s system and of the joint system of Alice and Bob
C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J. A. Smolin, and W. K. Wootters, Phys. Rev. Lett. 76, 722 (1996)
C. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters, Phys. Rev. Lett. 70, 1895 (1993)
A. K. Ekert, Phys. Rev. Lett. 67, 661 (1991); C. H. Bennett, G. Brassard, and N. D. Mermin, 68, 557 (1992)
C. H. Bennett and S. J. Wiesner, Phys. Rev. Lett. 69, 2881 (1992)
A. Osterloh, L. Amico, G. Falci, and R. Fazio, Nature 416, 608 (2002)
W. H. Zurek, Rev. Mod. Phys. 75, 715 (2003)

About the Author

Matthias Christandl is assistant professor for theoretical and mathematical physics at the University of Munich. He holds a Ph.D. from the University of Cambridge in England, where he was a Research Fellow prior to coming to Munich. It is the goal of his research to develop and solidify the mathematical and physical understanding of the new possibilities emerging from quantum information science. A main focus of his work is the study of correlations and entropies of quantum systems, but his work also includes proposals for new cryptographic protocols.