Improving accuracy by leaps and unbounds

Sima Setayeshgar

Viewpoint

Improving accuracy by leaps and unbounds

Department of Physics, Indiana University, Bloomington, IN 47405, USA

June 14, 2010• Physics 3, 49

New analyses suggest strategies by which biological sensors may be able to measure changes in concentrations of chemical signaling molecules more accurately, but does this reflect what actually happens in nature?

Figure caption — **Figure 1:** Cells determine the concentration of signaling molecules (e.g., nutrients or toxins in the environment or intracellular transcription factors) by registering associated receptors as “bound” or “unbound” (the inset shows the receptor “readout” over time). As shown schematically for bacterial chemotaxis, a network of reactions transduces the external signal measured by cell surface receptors into a change in concentration of an intracellular protein, which is in turn measured by receptors at the base of the motor. This measurement biases the motor’s direction of rotation, which controls whether the cell runs or tumbles (changes direction). Cells compare the measurement of their external environment at a given time with their memory of it some time ago, and determine the temporal change. The work by Mora and Wingreen [1] shows that by monitoring the average unbound interval rather than the average binding occupancy, a biological receptor is able to reduce the uncertainty in the measurement process by a factor of two.

In the same way that arrangements of digital logic gates form the building blocks of electronic computers, networks of biochemical reactions constitute the computing hardware of cells. These networks carry out the processes of life, from cell growth and death to responses to environmental cues such as nutrients and toxins. Biological receptors—the cell’s “particle detectors”—measure the concentrations of external and internal signaling molecules, performing a generic and essential task of the cell’s computing machinery. Readouts from the receptors are used to regulate decision-making circuits within the cell that control the expression of genes and proteins, and cellular motion, growth and division.

The energy scale for biomolecular interactions is typically a few times $k_{B} T$ , so it is natural to ask: How reliably can these measurements be carried out in the face of inherent fluctuations? Do biological sensors reach the detection limits set by the laws of physics? Thierry Mora and Ned Wingreen at Princeton University in the US report theoretical results in Physical Review Letters [1] that add to recent efforts exploring these questions. Specifically, they suggest cells may be able to measure changes in time in the concentration of signaling molecules twice as accurately as previous theoretical bounds.

The ability to perform increasingly quantitative and noninvasive experiments on biological systems places us in an exciting era in which to look at cellular phenomena from the standpoint of statistical physics. We know of many examples where signal processing occurs with exceptional accuracy, such as the ability of rod photoreceptor cells to count single photons [2], the reproducibility of concentration profiles of morphogens (signaling molecules governing the pattern of tissue development in the embryo) and the accuracy with which they can be read out by cells [3], and the sensitivity of the bacterial flagellar motor to changes in concentration of an internal signal [4,5]. In these examples, the reliability of the output is limited by the inherent random nature of the input signal—photon shot noise or diffusive counting noise—thereby approaching a physical lower limit. The requirement of nearly perfect detection and processing of the input to generate the macroscopic output poses constraints on the underlying strategies, resulting in the adoption of common signal processing approaches in these biological systems [3,6].

Roughly thirty years ago, Berg and Purcell derived statistical limits of cell sensing in their classic article on the physics of chemoreception [7]. Their work focused on chemotaxis, the behavioral response of single-celled organisms that helps them move toward favorable chemicals and away from harmful ones. (Chemotaxis is involved in the motile response of immune cells hunting down bacterial predators, wound healing, the spread of cancerous cells, sperm navigation, and the preferential growth of neurons.) This canonical sensory response is best studied in the well-controlled and experimentally accessible setting offered by two model organisms. The eukaryotic social slime mold Dictystelium discoidium (or Dicty) and the prokaryotic bacterium Escherichia coli employ very different methods of chemotactic sensing and response and have emerged as “hydrogen atoms” in the study of cellular sensing.

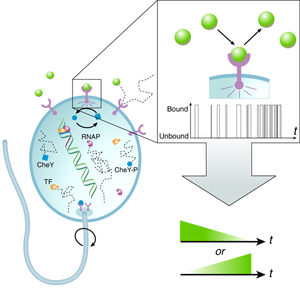
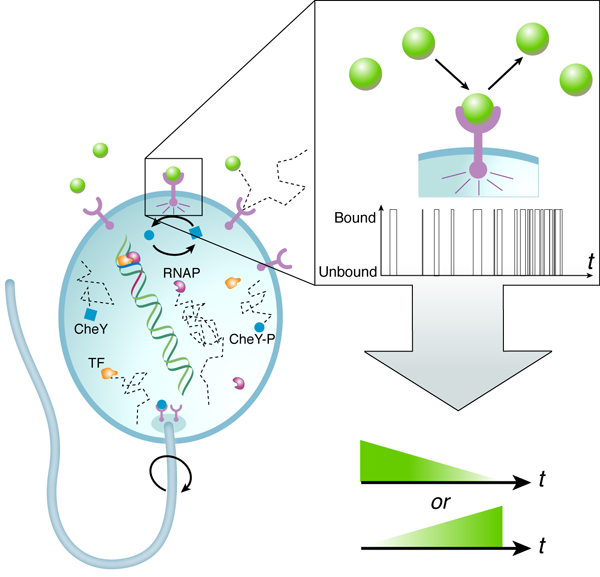
A central result from Berg and Purcell’s work was that the accuracy with which cells can detect the concentration of signaling molecules is fundamentally limited due to the random arrival of diffusing signaling molecules at their targets. A hypothetical “perfect” device, able to count molecules exactly, is limited by this diffusive noise only. In actuality, biological sensors “count” the number of diffusing signaling molecules by registering chemical binding and unbinding interactions (Fig.1). Thermal fluctuations in the free energy levels of the bound and unbound receptor-signal system lead to effective binding/unbinding reaction rate fluctuations and result in additional counting error. This means that in addition to the inherent noise in the signal, the measurement device itself is noisy.

Berg and Purcell considered these two contributions separately; more recently, the measurement accuracy of a chemical receptor was derived within the framework of statistical mechanics using the fluctuation-dissipation theorem, naturally incorporating both terms [4]. Building on earlier work by Endres and Wingreen [8,9], now in the context of sensing a time-varying concentration, Mora and Wingreen show that the noise inherent in the measurement device can, in principle, be reduced by a factor of two.

How is the twofold increase in accuracy achieved? Earlier works [4,7] assumed that a biological receptor infers the concentration of a signal by monitoring its equilibrium binding occupancy over some measurement time—the higher the average fractional occupancy of the receptor during this time, the higher the concentration of the signal. This is equivalent to using the average bound time (or equivalently, the average unbound time) to determine the signal concentration. Mora and Wingreen show that if, instead, the biological sensor uses only the average unbound intervals, the uncertainty of temporal gradient sensing is halved. In doing so, they extend the approach of Endres and Wingreen [9] from concentration to ramp sensing. Intuitively, this factor of two comes from the fact that in determining the average bound time, the measurement accuracy is subject to noise in both the bound and unbound intervals. However, only the average duration of unbound intervals carries information about the concentration of the input signal, while that of the bound intervals, which depends only on the unbinding rate, is independent of the input concentration. The notion that consideration of the information present in the unbound intervals gains a factor of two in accuracy, relative to that of the average bound time, has also been demonstrated within the past year by Endres and Wingreen [9] and by Mortimer et al. [10], where the latter work addresses temporal sensing in the context of neuronal growth cones.

Using a simple deterministic biochemical model that resembles the E. coli chemotaxis network, Mora and Wingreen show that “burst signaling”—rather than “continuous signaling,” which monitors the equilibrium receptor binding occupancy—allows greater accuracy in sensing temporal concentration changes. This mechanism approximates the average unbound interval in the limit of fast unbinding. Importantly, they argue that the gain in accuracy requires free energy consumption in the binding/unbinding cycle. Indeed, it is a common theme in biological signal processing that higher fidelity in enzymatic reactions is achieved through the addition of irreversible reaction steps and required energy consumption. The seminal example is that of kinetic proofreading schemes responsible for the remarkable accuracy of DNA replication and protein synthesis [11].

It’s fair to ask if burst signaling—as a mechanism for more accurately measuring the concentration of a signal—occurs in real biological systems. E. coli chemotaxis relies on continuous signaling, not the strategy put forth by Mora and Wingreen. However, an intriguing application of their work may be in understanding sperm cell chemotaxis in response to chemical gradients released by egg cells: Experiments suggest a connection between intracellular ${Ca}^{2^{+}}$ bursts and the cell’s chemotactic response [12]. Additionally, Mora and Wingreen speculate their work may be relevant to bursting kinetics in ligand-gated ion channels involving irreversible reaction steps [1]. These and other possible experimental connections remain to be confirmed. It will be interesting to see whether in these applications, the higher accuracy of this measurement process allows the overall macroscopic performance of the system to come down to the physical limit of diffusive counting noise.

References

T. Mora and N. S. Wingreen, Phys. Rev. Lett. 104, 248101 (2010)
F. Rieke and D. A. Baylor, Rev. Mod. Phys. 70, 1027 (1998)
T. Gregor, D. W. Tank, E. F. Weischaus, and W. Bialek, Cell 130, 153 (2007)
W. Bialek and S. Setayeshgar, Proc. Natl. Acad. Sci. USA. 102, 10040 (2005)
W. Bialek and S. Setayeshgar, Phys. Rev. Lett. 100, 258101 (2008)
W. Bialek, Ann. Rev. Biophys. Chem. 16, 455 (1987)
H. C. Berg and E. M. Purcell, Biophys. J. 20, 193 (1977)
R. G. Endres and N. S. Wingreen, Proc. Natl. Acad. Sci. USA 105, 15749 (2008)
R. G. Endres and N. S. Wingreen, Phys. Rev. Lett. 103, 158101 (2009)
D. Mortimer, P. Dayan, K. Burrage, and G. J. Goodhill, Physica D 239, 477 (2010)
J. J. Hopfield, Proc. Natl. Acad. Sci. USA 71, 4135 (1974)
K. Shiba, S. A. Baba, and M. Yoshida, Proc. Natl. Acad. Sci. USA 105, 19312 (2008)

About the Author

Sima Setayeshgar received her Ph.D. in 1998 from the Physics Department at the California Institute of Technology. She was a Princeton University Council on Science and Technology Postdoctoral Fellow before joining the Physics Department faculty at Indiana University, Bloomington. Sima’s research focus is in theoretical and computational biological physics. Her work spans areas from pattern formation in nonequilibrium systems at the macroscopic scale to physical principles governing biochemical signaling networks at the microscopic scale. Her research is funded by the NSF, most recently as a recipient of a Faculty Early Career Award in 2007.