Imaging matter in different spaces

Ian Robinson

Viewpoint

Imaging matter in different spaces

London Centre for Nanotechnology, University College London, Gower St., London WC1E 6BT, United Kingdom
Research Complex at Harwell, Didcot, Oxfordshire OX11 0FA, United Kingdom

March 14, 2011• Physics 4, 22

An x-ray free electron laser setup converts the diffraction pattern of randomly positioned and oriented particles into an image of a single particle.

Figure caption — **Figure 1:** Illustration of the coherent scattering pattern expected from (left) a single rod-shaped particle and (center) a dilute random collection of rod-shaped particles in solution. (Right) Schematic scattering of rod-shaped virus particles, redrawn from Z. Kam *et al.* [11].

Correlation functions in real space play a central role in condensed matter physics [1]. Historically prevalent in the physics of phase transitions, the correlation function has emerged as a key connection between experiment and theory. For example, important measurements of critical exponents and the discovery of new phases, such as the hexatic phase of liquid crystals [2], have followed directly from the accessibility of the correlation function through x-ray and neutron scattering [3]. The assumptions are modest: the Born approximation, which guarantees a linear response, and a basic knowledge of the instrument response.

What is traditionally measured in scattering experiments is the two-point density correlation function of the material under study, because this is proportional to the scattering intensity signal. It has therefore become the basic objective of theoretical calculations, so that they can be compared with experiment. This correlation function is the probability that two atoms are a given distance apart and it informs us about the pair-distribution averaged over all the atoms; x-ray resonance effects can then be used for chemical specificity.

Higher-order correlation functions, particularly four-point functions, are sensitive to the alignment of bonding arrangements between atoms and how rapidly these decay with distance. This information is vital in the study of amorphous materials that are increasingly useful in communications, environmental, and energy technologies. Potentially, these functions could probe more exotic properties of materials, such as chirality, on the atomic or nanometer length scale. Future research into the emergence of chirality in complex systems due to asymmetric external fields could be envisioned, for example. But higher-order correlation functions cannot be measured in simple scattering experiments, with the benefit of their simplifying assumptions regarding reciprocal space, and so have to be evaluated in real space. This is why the development of imaging methods is so important in physics. Once powerful new imaging methods are available, higher-order correlations are expected to be of renewed interest. Indeed, this is beginning with the introduction of “fluctuation microscopy,” which is a real-space method for analyzing the variations found in electron microscope images of amorphous materials [4].

The emergence of electron microscopy in the 1950s opened the possibility of imaging defects and inhomogeneities that led directly to the foundation of materials science as a discipline, uniting previously separate subjects such as ceramics, metallurgy, and polymer science. But electron microscopy is largely two dimensional (2D), though it is currently evolving towards 3D for precisely the reasons stated above. Meanwhile, x-ray imaging is rapidly realizing the possibility of fully 3D imaging of relatively large volumes of material.

X-ray tomography, analogous to the medical CAT scan, has moved into the domain of phase contrast by the use of phase gratings [5]. The technique of coherent diffractive imaging (CDI) avoids the limitations of x-ray lenses through the use of computational algorithms that invert the diffraction, and works well in 3D for compact structures [6]. For extended structures without well-defined boundaries, x-ray ptychography [7] has filled the gap between CDI and tomography and is now working in 3D [8].

X-ray imaging is likely to remain a mesoscale technique, with its strengths in the $10 nm$ resolution range. This is largely limited by radiation damage, which is more serious than for electron diffraction or microscopy. While the x-ray free electron laser (XFEL) facilities offer some hope of beating the damage by using short-lived femtosecond pulses, the atomic resolution limit will probably remain largely with electron-based methods. That said, their well-known penetrating property means that x rays will retain their position of being the only way of evaluating the 3D distribution of matter in samples thicker than about a micron.

In a paper in Physical Review Letters [9], Dilano Saldin at the University of Wisconsin in Milwaukee and his coauthors report an exciting development–usage of reciprocal-space correlation functions to extract real-space structural information. Theirs is the first experimental confirmation of one of the ideas originated by Zvi Kam in the 1970s for x-ray scattering from dilute systems of identical particles [10,11], where the individual particles are illuminated coherently (to use the current language) while interparticle distances exceed the coherence length. As Saldin et al. show, the single-particle coherent diffraction pattern can be phased by computational algorithms, hence inverted by a Fourier transform to an image of the particle. A rich variety of algorithms have been developed over the past few years, originating from the work of Fienup [12]. Data are iteratively Fourier transformed from reciprocal to real-space and back, while applying constraints in both spaces: the measured diffraction in reciprocal space and some “density modification” in real space. For the latter, Saldin et al. chose to use a so-called charge-flipping method in which the phase of low-lying electron density is reversed. It was established in the work of Bates [13] that in 2D and 3D the “oversampled” bandwidth-limited scattering amplitude (with missing phases) has a unique inverse in all but a few “pathological” cases where the amplitude function can be factorized.

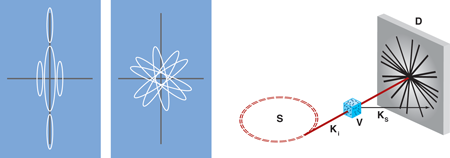
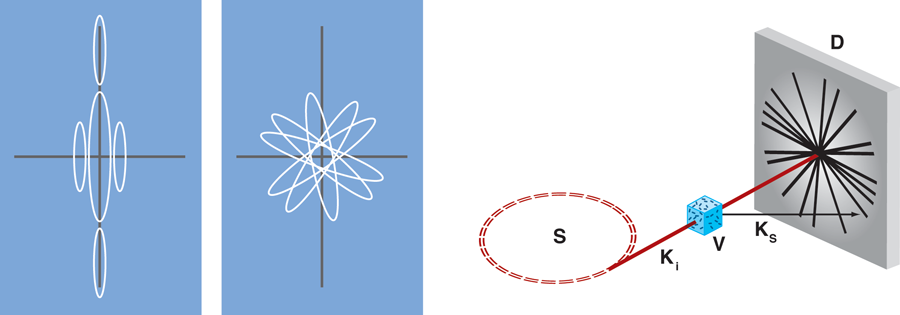
The innovation in Saldin et al.’s paper is the extraction of the single-particle coherent diffraction pattern from the superposition of many copies of it that have different random orientations [14]. As illustrated in Fig. 1, the diffraction pattern measured from a small number of isolated particles is the intensity superposition of multiple single-particle patterns. Reverting to the pattern of just one particle is achieved by evaluating the angular correlation function of the many-particle scattered intensity, divided into thin shells of reciprocal space. This is then Fourier transformed and transformed back again to the reciprocal space intensity distribution, after applying the assumption that the Fourier modulus is real and positive in each shell. A smoothing step is used to fill in the missing data around the beam stop needed for the measurement. The paper presents clear images of $90 \times 25 nm$ rod-shaped nanoparticles, measured by x-ray scattering while randomly distributed in 2D on a supporting membrane. Kam’s original application, also shown in Fig. 1, was for solutions of rod-shaped tobacco mosaic virus particles of similar dimensions, for which the 3D extension of Saldin’s method would be admirably suited [10]. Alternatively, if the virus particles are diluted further, snapshot views of individual particles could be obtained with a sufficiently powerful source, as has recently been achieved at the XFEL at Stanford [15].

The same angular correlation function used by Saldin et al. has been applied to study orientational order in colloidal glasses [16]. The coherent x-ray diffraction pattern of a concentrated suspension of polymethylmethacrylate (PMMA) particles was dissected into narrow radial shells. At certain radii of reciprocal space, the angular correlations were found to show fivefold symmetry, in addition to the expected four- and sixfold symmetries. This suggests that the colloidal particles have fivefold packing on those corresponding distance scales in real space. This powerful x-ray method, and its generalization [17], could be extended to the atomic resolution structure of amorphous materials, already under investigation by electron diffraction in fluctuation microscopy [4]. When combined with the ability to take snapshots of moving matter, using XFELs, these reciprocal-space angular correlation methods will enable widespread investigation of local order in liquids or more excited states of condensed matter.

References

Phase Transitions and Critical Phenomena, edited by C. Domb and M. S. Green (Academic Press, London, 1972)[Amazon][WorldCat]
R. Pindak, D. E. Moncton, S. C. Davey, and J. W. Goodby, Phys. Rev. Lett. 46, 1135 (1981)
Proceedings of the International Conference on Ordering in Two-Dimensions, Lake Geneva, Wisconsin, May 28-30, 1980, edited by S. K. Sinha (North-Holland, Amsterdam, 1980)
J. M. Gibson, M. M. J. Treacy, T. Sun, and N. J. Zaluzec, Phys. Rev. Lett. 105, 125504 (2010)
F. Pfeiffer, T. Weitkamp, O. Bunk, and C. David, Nature Phys. 2, 258 (2006)
Ian Robinson and Ross Harder, Nature Mater. 8, 291 (2009)
J. M. Rodenburg et al., Phys Rev. Lett. 98, 034801 (2007)
M. Dierolf, A. Menzel, P. Thibault, P. Schneider, P. C. M. Kewish, R. Wepf, O. Bunk, and F. Pfeiffer, Nature 467, 436 (2010)
D. K. Saldin, H. C. Poon, M. J. Bogan, S. Marchesini, D. A. Shapiro, R. A. Kirian, U. Weierstall, and J. C. H. Spence, Phys. Rev. Lett. 106, 115501 (2011)
Z. Kam, Macromolecules 10, 927 (1977)
Z. Kam, M. Koch, and J. Bordas, Proc. Natl. Acad. Sci. U.S.A. 78, 3559 (1981)
J. Fienup, Appl. Opt. 21, 2758 (1982)
R. H. T. Bates, Optik 61, 247 (1982)
D. K. Saldin et al., New J. Phys. 12, 035014 (2010)
M. Marvin Seibert et al., Nature 470, 78 (2011)
Peter Wochner et al., Proc. Natl. Acad. Sci. U.S.A. 106, 11511 (2009)
M. Altarelli, R. P. Kurta, and I. A. Vartanyants, Phys. Rev. B 82, 104207 (2010)

About the Author

Ian Robinson trained in biological crystallography with Steve Harrison at Harvard. He then moved to Bell Labs and the University of Illinois to work on new synchrotron diffraction methods for solving surface structures. His discovery of “crystal truncation rods” has led to the new field of surface x-ray diffraction, still widely used at synchrotron facilities all over the world. He then worked on developing the coherent x-ray diffraction (CXD) method at a beamline at the Advanced Photon Source in Chicago. In 2005 he moved to University College London and has been building CXD capabilities at the Diamond Light Source.