Mimicking Magnetic Fields in Optical Lattices
For decades, magnetic fields have been an indispensable tool for physicists to better understand the properties of condensed matter. For instance, only the discovery of the complete expulsion of magnetic fields from superconductors allowed for their description as thermodynamic states. Strong magnetic fields are required for the appearance of the quantum Hall effect, where the conductivity of two-dimensional electron gases becomes quantized and hence enables the precise measurement of fundamental constants of nature. More generally, gauge fields play a central role in the description of macroscopic quantum phenomena in strongly correlated condensed matter.
The dynamics of ultracold atoms trapped by a web of laser light can be made to resemble that of electrons moving through a crystal lattice. The lattice period is given by half an optical wavelength. The atoms tunnel quantum mechanically—preserving the phase of their wave function—from one lattice site to the next and strongly interact when occupying the same site. Optical lattices offer decisive advantages for studying models of strongly correlated quantum matter, like exact controllability of system parameters over a wide range and highly versatile experimental setups. Technical challenges arise from the need to achieve nanokelvin temperatures for quantum effects to become dominant and from comparatively slow dynamics on millisecond time scales. Furthermore, the motion of the electrically neutral atoms does not respond to electric and magnetic fields like electrons do.
Nevertheless, the rich physics arising when condensed matter is placed into magnetic fields is still accessible in optical lattices if one is able to mimic the effect of a magnetic field by other means. The quantum-mechanical effect of a magnetic field on the motion of charged particles is to imprint a Peierls phase onto their wave function when hopping between lattice sites, thus leading to a complex hopping parameter. The total phase attained by a charge moving through a closed loop is determined by the magnetic flux threading the area enclosed by the path. Now, presenting their work in Physical Review Letters, two groups [1,2], pursuing different approaches, have experimentally demonstrated the generation of complex hopping amplitudes.
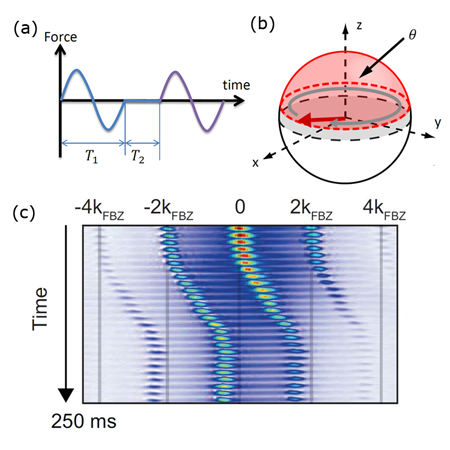
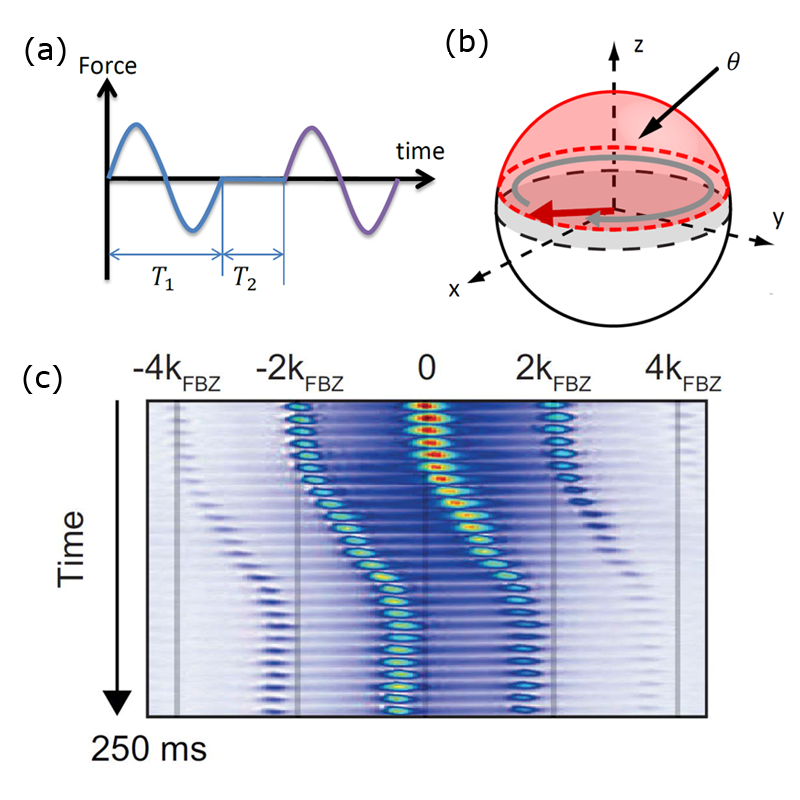
In the experiment by Julian Struck at the University of Hamburg, Germany and colleagues [1], the optical lattice is deformed by frequency modulating one of the lattice beams on time scales much faster than typical hopping times, which is experimentally straightforward. The modulation generates a time-dependent force that averages to zero [(see Fig. 1(a)]. By breaking reflection and shift symmetries of the force’s time dependence, a Peierls phase, which smoothly and monotonously increases with the amplitude of the force, is induced. Importantly, this technique is independent of the internal structure of the atoms. The setup is thus expected to work for a wide range of quantum particles trapped in lattice potentials that can be forced sufficiently fast.
Karina Jiménez-García and colleagues at the Joint Quantum Institute, the University of Maryland, College Park and NIST [2], achieve a similar goal by following a different approach—explicitly exploiting the internal atomic structure and blurring the concept of first creating an optical lattice and then modifying its hopping parameters. Instead, they use a combination of Raman lasers and radio frequency fields to reach both goals simultaneously, following ideas similar to those first presented by Dum and Olshanii [3] in 1996. The experiment utilizes the ground state manifold of for which the laser and radiofrequency fields induce a spatially varying effective magnetic field. A geometric Berry phase equal to the solid angle subtended by the field in a tunneling event is imprinted onto the atomic wave function, thus generating the required complex hopping amplitude as shown in Fig. 1(b).
Both experiments demonstrate their respective method for optical lattices in one spatial dimension where the only visible effect of a Peierls phase is to shift the minimum of the band structure to a finite lattice quasimomentum . This shift is measured in both experiments by adiabatically changing and measuring the change in quasimomentum [shown in Fig. 1(c)] in a time-of-flight setup, which maps momentum states onto atom positions. In addition both experiments realize abrupt changes in and study the relaxation of the atoms to the new minimum of the band structure. Finally, the magnitude of the hopping amplitude and corresponding effective mass of the atoms are measured by inducing oscillations in the atom cloud. In both experiments, excellent agreement with theoretical predictions is obtained in all of these measurements, demonstrating clearly their ability to accurately emulate the effects of gauge fields in optical lattices.
However, it should also be pointed out that these experiments are well explained by single-particle physics. Atom-atom interactions are insignificant for the obtained results. The most intriguing many-particle magnetic phenomena rely on weak exchange-type interactions. Thus, in addition to very stable and well-controlled Hamiltonian parameters demonstrated in the current experiments, extremely low temperatures as well as exquisite control over particle numbers and background trapping potentials are required for these effects to become visible.
In both papers, the authors also discuss how to potentially extend their setups to two spatial dimensions. They show how staggered magnetic fields whose flux averages out over sufficiently many lattice sites could be produced. While in one dimension a change of reference frame removes Peierls phases, this is not possible in two spatial dimensions, leading to much richer physics. For instance, magnetic frustration in a triangular lattice has recently been observed in an experimental simulation of classical magnetism by Struck et al. [4]. With access to novel schemes for controlling Peierls phases, they may now be able to extend these studies to observe true quantum frustrated many-body dynamics. Similarly, recent experiments by LeBlanc et al. [5], demonstrating the Hall effect in superfluid ultracold atoms might benefit from these new technologies.
Experimental efforts with the aim of studying quantum magnetism in optical lattices are currently on-going in several groups. For instance, a recent experiment by Aidelsburger et al. [6] has generated Raman-laser-imprinted staggered magnetic fields in two-dimensional lattices (see 12 December 2011 Viewpoint). They combined these techniques with single-site resolution to directly observe the microscopic atomic motion around a closed loop of the lattice.
All of these recent experiments constitute impressive steps towards simulating many-body quantum dynamics in gauge fields by explicitly engineering the microscopic interactions of ultracold atoms with light. Further progress will soon require full control over spin-dependent exchange interactions between atoms and may be even more challenging to achieve. Yet, the potential reward of gaining an improved understanding of quantum magnetism in strongly correlated quantum systems, which still holds many secrets, will be worth these efforts.
References
- J. Struck, C. Ölschläger, M. Weinberg, P. Hauke, J. Simonet, A. Eckardt, M. Lewenstein, K. Sengstock, and P. Windpassinger, Tunable Gauge Potential for Neutral and Spinless Particles in Driven Optical Lattices, Phys. Rev. Lett. 108, 225304 (2012)
- K. Jiménez-García, L. J. LeBlanc, R. A. Williams, M. C. Beeler, A. R. Perry, and I. B. Spielman, Peierls Substitution in an Engineered Lattice Potential, Phys. Rev. Lett. 108, 225303 (2012)
- R. Dum and M. Olshanii, “Gauge Structures in Atom-Laser Interaction: Bloch Oscillations in a Dark Lattice,” Phys. Rev. Lett. 76, 1788 (1996)
- J. Struck, C. Ölschläger, R. Le Targat, P. Soltan-Panahi, A. Eckardt, M. Lewenstein, P. Windpassinger, and K. Sengstock, “Quantum Simulation of Frustrated Classical Magnetism in Triangular Optical Lattices,” Science 333, 996 (2011)
- L. J. LeBlanc, K. Jiménez-García, R. A. Williams, M. C. Beeler, A. R. Perry, W. D. Phillips, and I. B Spielman, ”Observation of a Superfluid Hall Effect," arXiv:1201.5857v1
- M. Aidelsburger, M. Atala, S. Nascimbène, S. Trotzky, Y.-A. Chen, and I. Bloch, “Experimental Realization of Strong Effective Magnetic Fields in an Optical Lattice,” Phys. Rev. Lett. 107, 255301 (2011)