The Choreographer of a Most Unusual Electron Dance

Neepa T. Maitra

Viewpoint

The Choreographer of a Most Unusual Electron Dance

Department of Physics and Astronomy, Hunter College and the City University of New York, 695 Park Avenue, New York, NY 10065, USA

July 16, 2012• Physics 5, 79

A new approach to finding the electronic potentials in density-functional theory—one of the most important computational tools in condensed matter and quantum chemistry—is proposed.

Figure caption — **Figure 1:** Kohn-Sham potentials give the right electron density in an interacting system, even though the electrons are treated as independent particles. (Top) An example from the simplest system of interacting electrons: the helium atom. The top curve is the ground-state electron density. The lower curves show (orange) the nuclear potential, $- 2 / r$ (in atomic units), that the electron lives in, and the (blue) Kohn-Sham potential, which is the potential in which noninteracting electrons yield the same density. (Bottom) Schematic of the time-dependent part of the Kohn-Sham potential (blue) of an electron wave packet (grey) propagating in a model semiconductor. The time-dependent part of the potential has a highly nonlocal dependence on the density: the potential to the left and right of the electron differ by a step, persisting far on either side. The size of the step oscillates in time. (For simplicity, modulations due to the lattice periodicity are omitted in the figure.)

Imagine being able to calculate the exact quantum mechanics of electrons in an atom, molecule, or solid by completely removing the Coulomb repulsion between the electrons and warping the attraction between the electrons and the nuclei. Doesn’t this sound crazy? Yet this is exactly the recipe for the remarkably successful, and rigorous, density-functional theory (DFT), which says that one can extract the correct observables of an interacting electronic system by instead treating the electrons as independent particles that interact with a fictitious potential.

Formulated in 1964, DFT has revolutionized electronic structure calculations in materials science and quantum chemistry [1,2]. The younger, time-dependent extension of DFT, TDDFT, is used to treat electrons that start in nonstationary states or that are subject to external fields [3,4]. But what is the right way to “warp” the attractive nuclear potential so as to choreograph the noninteracting electrons, whose dance contains all the exact information about the true time-dependent system? Except for a handful of calculations limited to model systems with two electrons, the answer to this question has largely gone unexplored. In Physical Review Letters, James Ramsden and Rex Godby of the University of York, UK, present an algorithm for finding the choreographer—otherwise known as the exact time-dependent Kohn-Sham potential—and apply it to a model semiconductor containing a moving electron [5]. They find that the Kohn-Sham potential for this case has several features that the approximations in today’s TDDFT simulations neglect. Understanding these features leads the way to building better TDDFT approximations for other systems.

TDDFT is an exact reformulation of the quantum dynamics of systems of many identical (nonrelativistic) particles. It states that all observables may be extracted from two quantities: the initial wave function and the time-dependent one-body density, $n (r, t)$ , which is the probability of finding any one particle at point $r$ in space at time $t$ . The time-dependent correlated many-body wave function, which is exponentially expensive to calculate as the number of particles grows, is not needed. Instead, TDDFT maps a system of interacting electrons into a system of fictitious noninteracting “Kohn-Sham” fermions, which reproduces the true time-dependent one-body density.

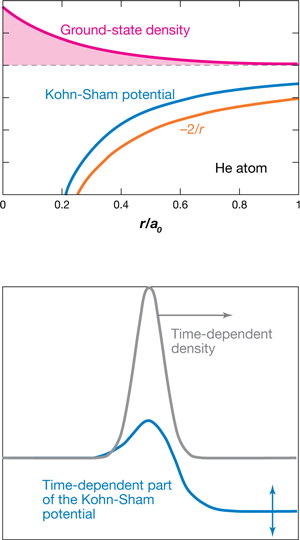
Since only single-particle orbitals need to be calculated, TDDFT makes it computationally possible to study the excitations and dynamics of systems containing many electrons. The challenge is to find the potential in which noninteracting electrons evolve with the same density as that of the true interacting electronic system (see Fig. 1, top, for a simple example.) The Kohn-Sham potential is the sum of three terms: the external potential applied to the true electrons (from the nuclei and any external scalar fields), the Hartree potential [the classical electrostatic repulsion of an electron cloud of density $n (r, t)$ ], and the exchange-correlation potential. This last term represents all the many-body effects beyond the mean-field Hartree term and is unknown. Instead, it must be approximated as a functional of the time-dependent density, initial interacting wave function, and initial Kohn-Sham wave function, meaning these ingredients uniquely specify the potential everywhere in space at all times. Typically, one inserts the instantaneous density into approximations of the ground-state problem (adiabatic approximation). The exact time-dependent functional, however, does depend on the history of the density, as well as on the initial wave functions. Further, there are many ground-state approximations. The problem is that we don’t really have a good understanding of the errors that result from making all of the approximations. If we could find the exact potential for at least a few problems, we’d gain this understanding, and maybe improve the approximations we use for general problems, and the predictive power of TDDFT.

This is what Ramsden and Godby do. They consider an electron propagating through a semiconductor, a problem that’s fundamental for understanding charge transport, a topical application of TDDFT. An exact solution of Schrödinger’s equation for this system is not available. Instead, Ramsden and Godby treat an approximate solution of many-body interacting quantum mechanics as the reference solution, and then ask what Kohn-Sham potential achieves the same time-evolving density as this reference by propagating noninteracting electrons. In the initial state, a moving electron is placed in a periodic lattice of one-electron atoms. The authors iterate toward an exact Kohn-Sham potential using a clever algorithm to systematically correct a guessed potential: the current-density of the Kohn-Sham system at time $t$ , $j_{s} (r, t)$ , is, at each iteration, corrected towards that of the true system, $j (r, t)$ , via the addition of a vector potential $A_{s} (r, t) = (j (r, t) - j_{s} (r, t)) / n (r, t)$ . Only a one-dimensional model is considered, so all vector potentials can be transformed to a scalar potential.

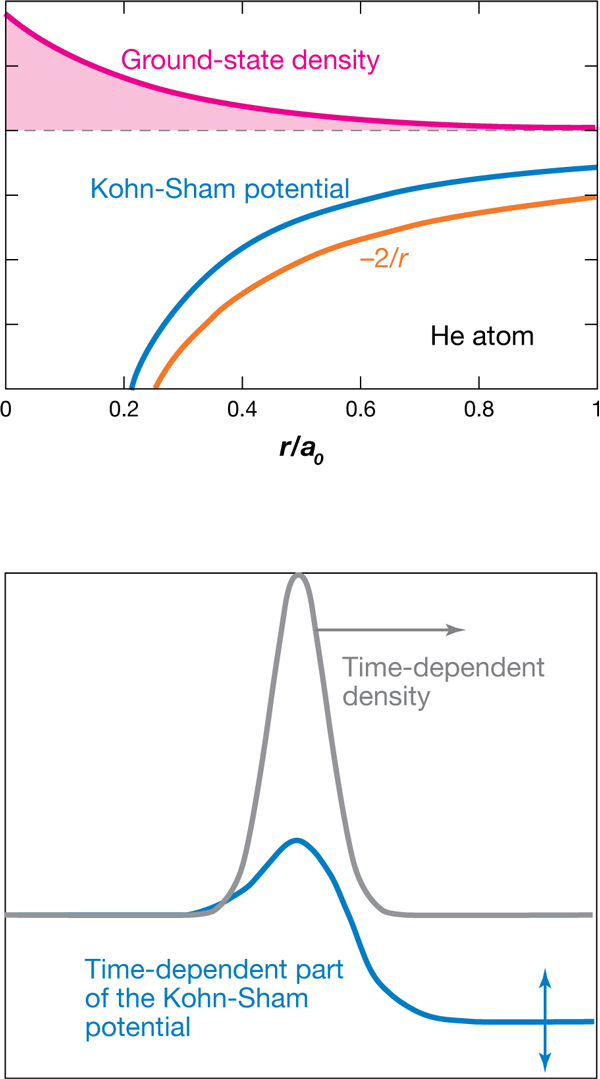
What the authors find is that the exact Kohn-Sham potential is lower in the entire region in front of the electron wave packet relative to the region behind the wave packet (Fig. 1, bottom). The size of this potential “step” is time-dependent and persists far away from the wave packet where the density is the unperturbed ground-state one, indicating that the potential depends on density infinitely far away. The ultranonlocal density dependence appears in the exchange-correlation potential—the term that must be approximated. However, most approximations miss this nonlocal property completely.

Step features have appeared before in DFT, such as in the exact ground-state potential of dissociating heteroatomic molecules [6,7], and in ionization [8] and Coulomb-blockade phenomena [9]. In the system Ramsden and Godby study, there is no external field, the step is between two regions of the same electron number, and its size oscillates in time, unlike in the previous cases. The authors’ result therefore opens up the question of whether nonlocal potentials are a more general feature of TDDFT.

Time nonlocal density dependence is also an important feature of the exact potential: an exchange-correlation functional that only depends on the instantaneous density won’t work, since an electron with the same density could be launched in the opposite direction, but the potential would have a step of the opposite sign.

One approach to incorporate spatially ultranonlocal and time-nonlocal density dependence is time-dependent current-density-functional theory (TDCDFT), where one deals with vector potential functionals of the current density [10]. (Actually, Ramsden and Godby’s procedure applied in three dimensions generally would fall into TDCDFT, not TDDFT, as TDDFT uses only scalar potentials). How well the approximate functional of Ref. [10] performs for Ramsden and Godby’s example is an interesting question for the future. Future studies will also need to understand how the Kohn-Sham potential depends on the choice of the initial Kohn-Sham wave function [11] [it only needs to reproduce the exact interacting $n (r, 0)$ and the longitudinal part of $j (r, t)$ , and there may be a choice where the usual approximations fare best]. It’s also possible that the observed features in the potential will change with more accurate solutions to the approximate many-body problem used as reference.

TDDFT has become a method of choice to compute excitation spectra in molecules, solids, clusters, and biomolecules. Applications to transport, the real-time dynamics of electrons evolving under strong laser fields, or the coupled electron-nuclear dynamics that follow photoexcitation (e.g., in modeling solar cell processes) are particularly enticing for TDDFT as there are very few alternative methods for studying these systems that are both computationally feasible and adequately capture electron correlation. So far, TDDFT’s progress in tackling these sorts of problems has been slow, partly because there aren’t many accurate calculations to check the TDDFT predictions. If the exact (or accurate) solution is known for a given problem, finding the exact time-dependent exchange-correlation potential via the scheme presented by Ramsden and Godby will be extremely useful, enabling us to see shortcomings of the usual exchange-correlation approximations and what we need to do to improve them.

References

P. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Phys. Rev. 136, B864 (1964)
W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Phys. Rev. 140, A1133 (1965)
E. Runge and E. K. U. Gross, “Density-Functional Theory for Time-Dependent Systems,” Phys. Rev. Lett. 52, 997 (1984)
Fundamentals of Time-Dependent Density Functional Theory, edited by M. A. L. Marques, N. T. Maitra, F. Nogueira, E. K. U. Gross, and A. Rubio, Lecture Notes in Physics Vol. 837 (Springer, Berlin, 2012)[Amazon][WorldCat]
J. D. Ramsden and R. W. Godby, ”Exact Density-Functional Potentials for Time-Dependent Quasiparticles,” Phys. Rev. Lett. 109, 036402 (2012)
C. O. Almbladh and U. von Barth, “Exact Results for the Charge and Spin Densities, Exchange-Correlation Potentials, and Density-Functional eigenvalues,” Phys. Rev. B. 31, 3231 (1985)
J. P. Perdew in Density Functional Methods in Physics, edited by R. M. Dreizler and J. daProvidencia (Plenum, New York, 1985)[Amazon][WorldCat]
M. Thiele, E. K. U. Gross, and S. Kümmel, “Adiabatic Approximation in Nonperturbative Time-Dependent Density-Functional Theory,” Phys. Rev. Lett. 100, 153004 (2008)
S. Kurth, G. Stefanucci, E. Khosravi, C. Verdozzi, and E. K. U. Gross, “Dynamical Coulomb Blockade and the Derivative Discontinuity of Time-Dependent Density Functional Theory,” Phys. Rev. Lett. 104, 236801 (2010)
G. Vignale and W. Kohn, “Current-Dependent Exchange-Correlation Potential for Dynamical Linear Response Theory,” Phys. Rev. Lett. 77, 2037 (1996)
P. Elliott and N. T. Maitra, “Propagation of Initially Excited States in Time-Dependent Density Functional Theory,” Phys. Rev. A. 85, 052510 (2012)

About the Author

Neepa Maitra did her undergraduate degree at the University of Otago in New Zealand, where she grew up. She obtained her Ph.D. at Harvard University, and after postdocs at the University of California, Berkeley, and Rutgers, she took a physics faculty position at Hunter College, City University of New York, where she does fundamental research in time-dependent density-functional theory. She sometimes uses model systems of two interacting particles to figure out exact properties of Kohn-Sham potentials, and her favorite system is her daughters. In this case, however, she can almost prove a Kohn-Sham potential does not exist.