Polariton Fluids for Optical Logic

Laura Pilozzi

Viewpoint

Polariton Fluids for Optical Logic

Laura Pilozzi

Istituto dei Sistemi Complessi, CNR, C.P. 10, Monterotondo Stazione, Roma I-00015, Italy

June 3, 2013• Physics 6, 64

Laser control of polariton current offers a new range of devices for all-optical logic circuits.

Figure caption — **Figure 1:** Tunneling transmission of cavity polaritons through a double barrier shows a characteristic intensity behavior, as a function of pump power $P_{gate}$ . When $P_{gate}$ is turned on, polariton-exciton interactions induce a shift in the polariton modes confined within the island. (a) When choosing for the incoming polariton flow energy $E_{inc}$ a value slightly larger than the energy of the first mode, no tunneling transmission is observed for low $P_{gate}$ values. (b) When the gate beam $P_{gate}$ equals the resonance power $P_{res}$ , the energy of the first cavity mode is brought into resonance with the polariton flow, the tunneling is quenched, and a pronounced increase in the transmission is induced. (c) When $P_{gate}$ slightly exceeds $P_{res}$ , vanishing transmitted signal is observed.

In the 1950s, Esaki [1] proved that electrons can penetrate through a barrier even though the passage is energetically forbidden according to classical mechanics; instead, the wave nature of quantum mechanics allows the electron to tunnel through the barrier. Today, Esaki’s discovery of resonant tunneling [2] is the basis of numerous high-frequency electronic devices [3]. Writing in Physical Review Letters, Hai Son Nguyen, at the Laboratory of Photonics and Nanostructures of the French National Center for Scientific Research in Marcousis, and colleagues now report [4] a new class of structures in which they achieve resonant tunneling of cavity polaritons—the fundamental optical excitations found in semiconductor microcavities—instead of electrons. Since they combine exciton and photon properties, polaritons have unique features that neither of their constituents has alone, offering opportunities to make new types of optical devices for logic operations [5].

Resonant tunneling of electrons [6] requires a double barrier forming a potential well and is distinguished by peaks in the tunneling current when the energy of the electrons, flowing from the source, coincides with one of the discrete energy levels in the well. Nguyen et al. studied cavity polaritons [7], which are light-matter quasiparticles responsible for the coupling between electron-hole pairs (excitons) and photons trapped in a semiconductor cavity on a micrometer scale. These microcavities act as photonic structures that enhance the interaction between light and matter: two mirrors confine the photons so they can resonantly interact with an excitonic transition. In the strong-coupling regime, the normal modes of this system are cavity polaritons. Because of their photonic component, polaritons are capable of moving at high speeds, up to $1 %$ of the speed of light, and can easily be excited by an external laser source and detected by light emission. At the same time, their excitonic component interacts with Coulomb forces, providing strong optical nonlinearities due to polariton-polariton interactions [8,9].

Polaritons are also bosons and thus can form a quantum condensate at temperatures ranging from a few kelvins in GaAs-based structures, up to room temperature in GaN- or ZnO-based semiconductor microcavities, owing to their very small effective mass. Recently, polariton Bose-Einstein condensation [10] and several fundamental properties of such condensates, such as superfluidity [11] and quantized vortices [12], have been reported. Several innovative devices have been proposed based on the control and manipulation of such condensates: thanks to their interactions with uncondensed excitons, polaritons can be accelerated to allow propagation over macroscopic distances [13]. Nevertheless, the very short polariton lifetime, only a few picoseconds, requires the use of high-quality quantum heterostructures.

Nguyen and colleagues are able to make microwire cavities of very high quality and, taking advantage of polariton condensation, they have fabricated an optical gate where the information is carried by flowing polaritons. The polaritons resonantly tunnel through a double potential barrier formed by tailoring the photonic potential of the cavity with a precise etching of the structure. Their system consists of $1$ D microwire cavities with a width of $3$ micrometers ( $μ m$ ) and a length of $440 μ m$ , created with electron-beam lithography and inductively coupled plasma dry etching of a GaAs/GaAlAs high-quality microcavity, significantly reducing the effect of disorder. Two micron-size constrictions are etched in the wires to create two tunnel barriers and define a $0$ D polariton island with discrete confined polariton states.

The researchers optically excite the wires with a nonresonant laser beam and polaritons, generated far from the island, spread out and propagate along the whole wire until they reach the double-barrier region, where they undergo resonant tunneling if their energy coincides with the energy of one of the confined modes. Changing the curvature of the polariton dispersion controls the group velocity of the expelled polaritons since it is inversely proportional to the square root of the polariton effective mass.

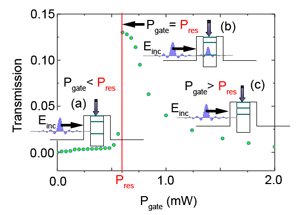
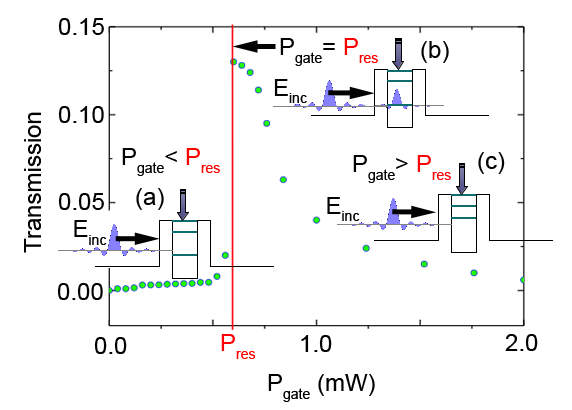
Optically injected excitons are the controlling factor in the flow of polaritons in this device. Nguyen and colleagues show that by manipulating a weak second laser beam of power $P_{gate}$ , focused on the island nonresonantly, they can modulate the resonant tunneling transmission with a peak-to-valley ratio as high as $28$ [4]. The mechanism is illustrated in Fig. 1. Note that the curve shows the characteristic intensity of the transmitted signal as a function of pump power $P_{gate}$ . The insets show the polariton flow propagation through the double barrier.

When $P_{gate}$ is turned on, polariton-exciton interactions induce a shift of the polariton modes confined within the island. When the gate beam, for $P_{gate} = P_{res}$ , brings the energy of the first cavity mode into resonance with the polariton flow, the tunneling is quenched, and a pronounced increase in the transmission is induced. On the other hand, the transmitted signal vanishes for $P_{gate} \neq P_{res}$ . Most remarkable is the transmission line shape for different $P_{gate}$ values, showing that, as a consequence of polariton-polariton interaction within the island, a nonlinear tunneling regime can be achieved for the device. Depending on the $P_{gate}$ to $P_{res}$ ratio, the system shows positive or negative feedback, which either helps or prevents the resonant tunneling, respectively.

This device is indeed operating as an all-optically-controlled resonant tunneling diode for cavity polaritons, with a very high spectral selectivity. Its operating frequency is of the order of gigahertz at present. However, based on simulations, the authors anticipate that the device performance may be significantly increased by properly adjusting the system characteristics, such as the barrier heights or the polariton lifetime.

Cavity polaritons are among the most intriguing excitations in semiconductor physics. The field is extremely rich in new fundamental effects that inspire much speculation on the possibility of starting a new generation of optoelectronic devices. The recent proposal of Nguyen et al. [4] is quite relevant in this context and can be seen as one of the building blocks for polaritonic circuits.

References

L. Esaki, “New Phenomenon in Narrow Germanium p-n Junctions,” Phys. Rev. 109, 603 (1958)
R. Tsu, “Tunneling in a Finite Superlattice,” Appl. Phys. Lett. 22, 562 (1973)
M. Feiginov, C. Sydlo, O. Cojocari, and P. Meissner “Resonant-Tunnelling-Diode Oscillators Operating at Frequencies above 1.1 THz,” Appl. Phys. Lett. 99, 233506 (2011)
H. S. Nguyen et al., “Realization of a Double-Barrier Resonant Tunneling Diode for Cavity Polaritons,” Phys. Rev. Lett. 110, 236601 (2013)
T. C. H. Liew, A. V. Kavokin, and I. A. Shelykh, “Optical Circuits Based on Polariton Neurons in Semiconductor Microcavities,” Phys. Rev. Lett. 101, 016402 (2008)
L. L. Chang, “Resonant Tunneling in Semiconductor Double Barriers,” Appl. Phys. Lett. 24, 593 (1974)
C. Weisbuch, M. Nishioka, A. Ishikawa, and Y. Arakawa, “Observation of the Coupled Exciton-Photon Mode Splitting in a Semiconductor Quantum Microcavity,” Phys. Rev. Lett. 69, 3314 (1992)
C. Ciuti, P. Schwendimann, and A. Quattropani, “Parametric Luminescence of Microcavity Polaritons,” Phys. Rev. B 63, 041303 (2001)
M. M. Glazov, H. Ouerdane, L. Pilozzi, G. Malpuech, A. V. Kavokin, and A. D’Andrea “Polariton-Polariton Scattering in Microcavities: A Microscopic Theory,” Phys. Rev. B 80, 155306 (2009)
J. Kasprzak et al., “Bose-Einstein Condensation of Exciton Polaritons,” Nature 443, 409 (2006)
A. Amo, J. Lefrère, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdré, E. Giacobino, and A. Bramati, “Superfluidity of Polaritons in Semiconductor Microcavities,” Nature Phys. 5, 805 (2009)
K. G. Lagoudakis, M. Wouters, M. Richard, A. Baas, I. Carusotto, R. Andréa, Le Si Dang, and B. Deveaud-Plédran, “Quantized Vortices in an Exciton-Polariton Condensate,” Nature Phys. 4, 706 (2008)
E. Wertz et al., “Spontaneous Formation and Optical Manipulation of Extended Polariton Condensates,” Nature Phys. 6, 860 (2010)

About the Author

Laura Pilozzi received her degree in physics from the University of Rome “Tor Vergata” in 1996. She is now a researcher at the Institute for Complex Systems of the Italian National Research Council (CNR). Her research interest is in theoretical condensed matter physics and photonics. The main themes of her work are related to radiation-matter interaction and polariton states of semiconductors and their heterostructures as microcavities and resonant photonic crystals and quasicrystals. Nonlinear optical effects and polariton scattering in microcavities are among her research subjects within the composed boson formalism for Wannier excitons.