When Does a Liquid Break Up?
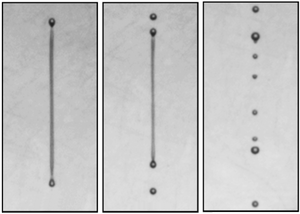
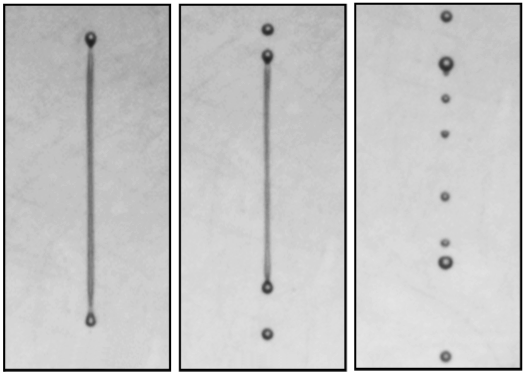
A thin stream of liquid can break up into many separate droplets, or it can collapse into one large drop. Reporting in Physical Review Letters, experimenters used a supersized version of an inkjet printer to explore how the viscosity and length of a liquid “filament” determine its fate. They measured a wide range of viscosities, and for each one, found the length at which the filament broke apart. The results confirm previous theoretical predictions overall, but there are small discrepancies. The research is important for a variety of fluid technologies, such as aerosol drug delivery and microfluidic devices used in biomedicine.
To optimize devices such as inkjet printers, researchers would like the ability to predict the fate of a stream of fluid in air. Computer simulations have confirmed the theoretical expectation that viscosity suppresses the breakup of a liquid filament, so that a more viscous filament can start out longer without breaking up. But researchers have only been able to test these theoretical ideas over a narrow range of viscosity.
One experimental challenge is that high viscosity makes it hard to create a long filament in the first place. Ian Hutchings and his team at Cambridge University in England solved this problem with their apparatus, which is similar to that used in inkjet printers. It can precisely squirt fluid through a nozzle in response to electrically-controlled pressure. The jet of fluid shoots downward out of the nozzle, although gravity plays no role in the process. The liquid filament can be monitored using high-speed cameras and other techniques because the nozzle is about a millimeter in diameter—much larger than nozzles used in commercial devices. The team has used their system in recent years to study many aspects of the inkjet process.
By using different mixtures of glycerol and water, together with other experimental changes, the researchers were able to vary the effective viscosity by a factor of nearly ten thousand. For each viscosity, they chose the time course of the pressure to make the machine produce uniform-looking filaments of various lengths. For some values of the viscosity, for example, they used a “push-pull” technique, sucking the liquid back through the nozzle to pinch off the filament.
The team recorded images of many filaments and built up a map of the lengths and viscosities that favor breakup and those that don’t. On their plot of length versus viscosity, there is a clear dividing line between the two regions. In comparison with the simulations, “it agrees, to the extent that the form of the curve separating breakup [from] no breakup is similar,” says Hutchings, “but the precise positions of that curve disagree from the theory.” Some discrepancy is not a big surprise, since the experiment may have fluid motions or other deviations from the ideal conditions assumed in the theory, and the simulations have their own limitations.
Osman Basaran of Purdue University in West Lafayette, Indiana, who contributed to the theory, agrees that the precise conditions that lead to breakup may still depend on uncontrolled details in the experiment. For example, small ripples on the liquid surface are “very important for people who make sprays.” But Basaran says that it is satisfying to see the experiments “finally done and done well.”
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.