Scenic Route for Sound Allows Extra Control
Physicists have discovered surprising ways to manipulate the propagation of waves, notably light, by using structures assembled from tiny elements. In Physical Review Letters, researchers propose to alter sound waves by diverting them through an array of narrow, circuitous channels, a method that wouldn’t work for light. Simulations confirm that so-called metamaterials composed of such channels have unusual properties that let them refract sound in the “wrong” direction and could improve ultrasonic imaging.
For years, researchers have been changing the way electromagnetic radiation travels by engineering materials with internal structures on the scale of the wavelength. In so-called photonic crystals, propagation of some waves is prevented by the cancellation of waves. More dramatic effects appear using arrays of tiny resonators that are tuned to respond strongly to the incoming wave frequency. Experiments have confirmed that these “metamaterials” can have exotic properties, like a negative index of refraction. They can be used in lenses that beat the usual limits on resolution and may even allow objects to be “cloaked,” making them appear invisible.
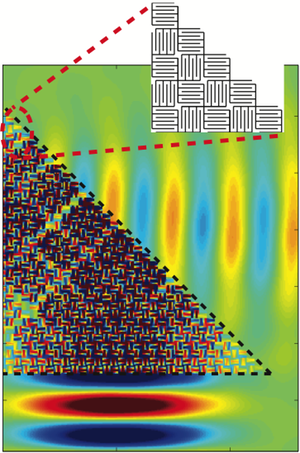
Researchers have recently extended these methods to acoustic waves. Such control might, for example, improve medical ultrasound imaging or protect buildings from earthquakes. Now Zixiang Liang and Jensen Li of the City University of Hong Kong propose a different kind of metamaterial that could work for sound but not for light. They imagine a two-dimensional region sliced into very small squares like a checkerboard. Within each square, a narrow sound “corridor” loops back and forth in a “maze” pattern to make a long path that fills up the square, with the entrance and exit at opposite corners. The team assumed there were two types of squares, identical except for a 90-degree rotation, arranged as the black and red squares on a checkerboard.
A sound wave (with wavelength larger than the squares) moving across the board gets delayed as it travels through the lengthy path within each square. The researchers focus on frequencies for which the path length is almost exactly a multiple of the wavelength. If the path is slightly longer, the wave emerges from the square at a point in its cycle only slightly delayed from when it entered, so the apparent speed of sound is very high, equivalent to an extremely small index of refraction. In contrast, at frequencies where the path is slightly shorter, the wave appears to exit before it enters. This situation leads to a negative effective index of refraction for the material, which is the same property that has allowed theorists to design super-resolution lenses and invisibility cloaks for light waves. But the principle of this new metamaterial wouldn’t work for light waves because they can’t ordinarily travel through a wave guide that is much narrower than their wavelength. Sound waves do this easily, as in a French horn, says Li.
The researchers confirmed with numerical simulations that a prism made of the metamaterial with a negative index of refraction bends sound in the opposite direction from ordinary refraction. Another simulation showed that for sound waves traveling in a straight pipe filled with an ordinary fluid, a barrier that blocks most of the cross section disrupts the passage of a wave. But with the metamaterial surrounding the barrier, the entire wave can reappear intact on the far side of the barrier, as though the barrier were invisible.
So far, the simulations are restricted to two dimensions, but Li notes that the principle extends easily to three dimensions. In addition, because there are no resonant structures storing large amounts of energy, the researchers hope that sound will propagate with relatively little loss. “The idea is quite original and very smart,” says Nicholas Fang of the Massachusetts Institute of Technology in Cambridge. But he cautions that experiments will be needed to find out if there are new loss mechanisms in these novel structures that would limit their usefulness.
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.