The Quantum of Heat Flow

Graham P. Collins

Focus

The Quantum of Heat Flow

July 9, 1998• Phys. Rev. Focus 2, 2

The thermal conductance of small wires is measured to take quantized values.

Figure caption — **Heat flow in a small wire.** For an extremely thin wire (red) at low temperatures the thermal conductance quantum has a universal value, independent of the wire’s shape, size and material. To observe this effect, the wire must join the thermal reservoirs (yellow, at temperatures $T_{1}$ and $T_{2})$ much more smoothly than is shown in this cartoon.

Physicists have known for over a decade that electrical conductance can be quantized: Under the right conditions it cannot have just any value, but comes only in units of the universal conductance quantum. In the past year, researchers have discovered that a similar quantization should occur for the conduction of heat. For an extremely thin wire at temperatures close to absolute zero, the heat conduction quantum should be “universal”–independent of the shape and size of the wire and even the material it is made of. In the 6 July PRL a pair of theorists puts this concept on an even firmer footing by showing that it should be observable in practical experiments.

Just as light waves can be described as collections of photons, the vibrations of a crystal lattice can be analyzed in terms of phonons, which can travel through a material, transporting energy in the form of heat. Luis Rego and George Kirczenow, of Simon Fraser University in Burnaby, Canada, show that the conductance of a thin, cold, phonon-carrying wire is quantized in units of $k^{2} p i^{2}$ T/3 h, where k is Boltzmann’s constant, T is temperature, and h is Plank’s constant. (The quantum of electrical conductance is $e^{2} /$ h, where e is the charge of the electron, and it occurs most famously in the quantum Hall effect.) The existence of the thermal quantum was deduced implicitly last year by Michael Roukes, of the California Institute of Technology, and his colleagues, but Rego and Kirczenow go on to analyze how an experiment could observe it.

One difficulty in observing the quantization of heat conduction experimentally is the effect of phonons reflecting from the points where the wire connects to the heat reservoir at each end. Rego and Kirczenow show that for a wire with square cross-section, these effects are minimized if the connection is extremely smooth. The flared bell of a trombone accomplishes a similar goal: it reduces internal reflections of the sound waves, allowing more sound to get out than if it were a straight tube.

The expression the team found for the thermal conductance quantum is identical to what others found for thermal conduction carried by electrons [1]. Kirczenow calls that result “stunning,” because electrons are fermions, and phonons are bosons–the two families of particles obey completely different fundamental rules.

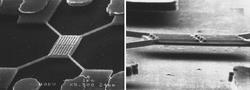
Roukes and his colleagues are currently working on the experiments analyzed by Rego and Kirczenow. In the past several years they have devised new techniques for fabricating nanostructures to study such tiny heat flows (see figure), and now, armed with the new analysis, they are modifying those experiments. Roukes believes those modifications will allow the thermal conductance quantum to be measured.

–Graham P. Collins

Graham Collins is a freelance science writer.