Triangular Hole Reveals Light’s Rotation
Light can carry “orbital angular momentum,” a kind of rotation that is more like a planet orbiting the sun than like the planet spinning on its own axis. Measuring this property is tricky, but in the 30 July Physical Review Letters, Brazilian researchers show that shining a beam through a triangular hole creates a triangular array of spots that directly indicates the orbital angular momentum of the beam. The simple technique adds another tool for exploring this unusual property of light, which might someday be used to encode quantum information.
When a beam of light carries angular momentum, it can have two contributions. The “spin” angular momentum corresponds to the right or left circular polarization of the light, meaning that the direction of the electric field rotates clockwise or counterclockwise as the light moves forward. “Orbital” angular momentum (OAM)–widely recognized only in the past 20 years–occurs if the direction of the electric field varies within the beam. For example, imagine measuring the electric field direction at each point around the edge of a large-diameter beam. It might point up at the top, to the right at three o’clock, downward at the bottom, and leftward at nine o’clock. This beam would have one unit of OAM–a “topological charge” of one. The field of a charge-two beam would go through two complete rotations as you move around the edge. Researchers hope to harness this property to carry information with light, just as they do with polarization [see Focus, 2002].
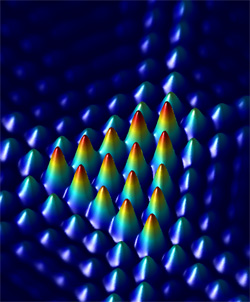
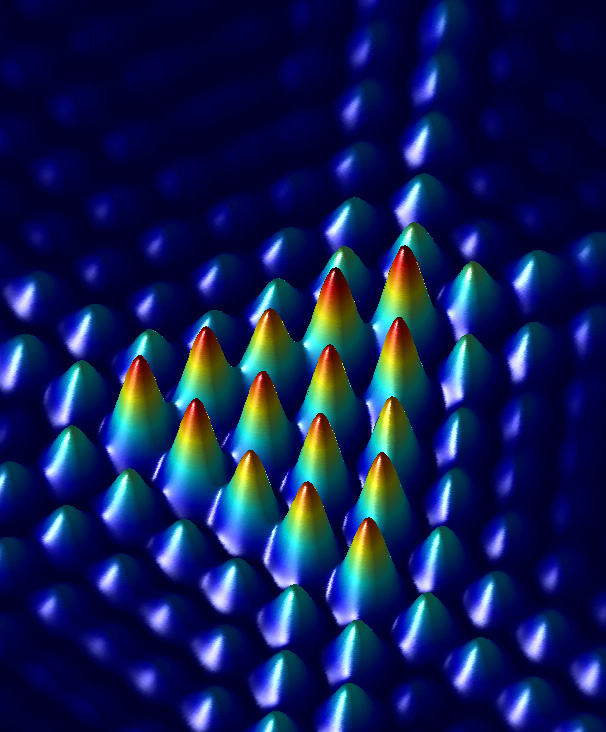
Physicists have learned how to make beams that have OAM and to use them to exert torque on particles. But Jandir Hickmann of the Federal University of Alagoas in Maceio, Brazil, says there has been surprisingly little research into what happens when these beams pass through small apertures. Such diffraction experiments generate patterns of spots that physicists have long used to reveal properties of ordinary light, but the techniques for measuring OAM are few and more complicated. When Hickmann and his colleagues simulated diffraction of beams passing through holes of various shapes, they found that using an isosceles triangle had an unexpected benefit: “you can just count the spots to find the topological charge.” The researchers also verified this prediction experimentally.
The team calculates and observes that, once the beam is centered on the hole, it generates an unusual pattern: a triangular lattice of spots. The brightness of individual spots depends on the combined light contributions from different places on the triangular hole. The calculations predict that the brightest spots form a triangle whose size (the number of spots on each side) is one greater than the magnitude of the topological charge. In addition, the bright triangle pattern is rotated by 60 degrees in either direction compared to the aperture, depending on the sign of the charge (the direction of the light’s rotation). So the triangular aperture gives an easy way to measure both the magnitude and sign of the orbital angular momentum.
Miles Padgett of the University of Glasgow, Scotland, says it “was a surprise (at least to me) that there should be such a beautiful and simple relationship” between the number of diffracted spots, the pattern’s orientation, and the magnitude and sign of the topological charge.
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.
More Information
Giving Light a New Twist (Focus, 2006)
Physics Today article “Light’s Orbital Angular Momentum” from 2004 (requires subscription)
Breaking Free of Bits (Focus, 2002)