Random Roads Less Travelled

Michael Schirber

Focus

Random Roads Less Travelled

August 5, 2011• Phys. Rev. Focus 28, 6

A uniform city street plan may produce heavy traffic everywhere, whereas a random network of road connections leaves some roads open, according to a mathematical model.

The tangled web of streets in old European cities might seem like a traffic nightmare. But a random network of connections may keep certain roads continuously free of congestion, according to a 5 August report in Physical Review Letters. The researchers compared different network structures, or “street maps,” using both mathematical models and computer simulations. Their observed distribution of high-traffic and low-traffic pathways may also explain the way certain proteins move around in a cell.

Traffic–a continuous flow of discrete objects–can move through city streets, over filament structures in cells, and across information highways like the Internet. Transport on these networks is difficult to model, since individual objects can interact with each other in complex ways. For example, drivers may speed up or slow down when they see other cars on the road, and these sorts of reactions can cause spontaneous traffic jams.

The totally asymmetric simple exclusion process (TASEP) is a well-studied traffic model that includes such interactions. This model stipulates that objects moving along a line segment (“road”) can only go in the specified forward direction, and no passing is allowed. These rules could apply, for example, to cars traveling on a one-way street with only a single lane, or to ribosomes “reading” the genetic code on a strand of RNA [1].

Researchers have studied TASEP in the simplest case of a single segment with an entry point at one end and an exit point at the other. The flow of objects through the segment depends explicitly on two probabilities: that of entering and that of exiting. “TASEP is controlled by the boundaries,” says Andrea Parmeggiani from the University of Montpellier 2 in France. If objects enter rarely, then the flow will be sparse and unobstructed. If objects exit rarely, then the traffic will completely back up. The flow is only high when objects can enter and exit with high probability, but even in this case traffic jams can spontaneously pop up.

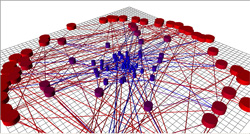
The picture becomes less clear when many segments are connected together. Simulating the movement of individual objects on large traffic networks can be computationally impractical, so Parmeggiani and his Montpellier colleagues devised a mathematical shortcut, where all the action is controlled by the junctions. If a junction is occupied, it can feed an object into one of its outgoing segments. If it’s empty, it can receive an object from one of its incoming segments. The researchers used this coupling between junctions and segments to mathematically solve for the average traffic density and flux on each segment in the network. They verified their results by comparing them with full simulations on moderately-sized networks.

The researchers first looked at “regular” networks, in which all of the junctions have the same number of connections, like a Manhattan cityscape. The traffic was essentially uniform, in that the density of objects was the same on every segment of the network. But in an irregular network, where different junctions have different numbers of connections, some segments were bumper-to-bumper–much worse than for a regular network–while others had minimal traffic. No segment had a density in between these extremes, but the overall average traffic flow was about the same as a regular network. As more cars were put into the network, the number of high-density segments increased, but “open roads” were always present. A distribution split into high and low density may describe the movement of proteins that carry cargo along microtubule networks inside cells, says Parmeggiani, and he’s collaborating with experimentalists to study this possibility.

The observation that irregular networks sort traffic into high- and low-traffic segments comes as a surprise, says Erwin Frey of the Ludwig Maximilian University in Munich. “At first sight one would have guessed that the most regular structure would optimize traffic,” Frey says. He thinks this sorting could serve a biological purpose in, for example, a cell that needs “fast lanes” and “slow lanes” for different types of cargo.

–Michael Schirber

Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.