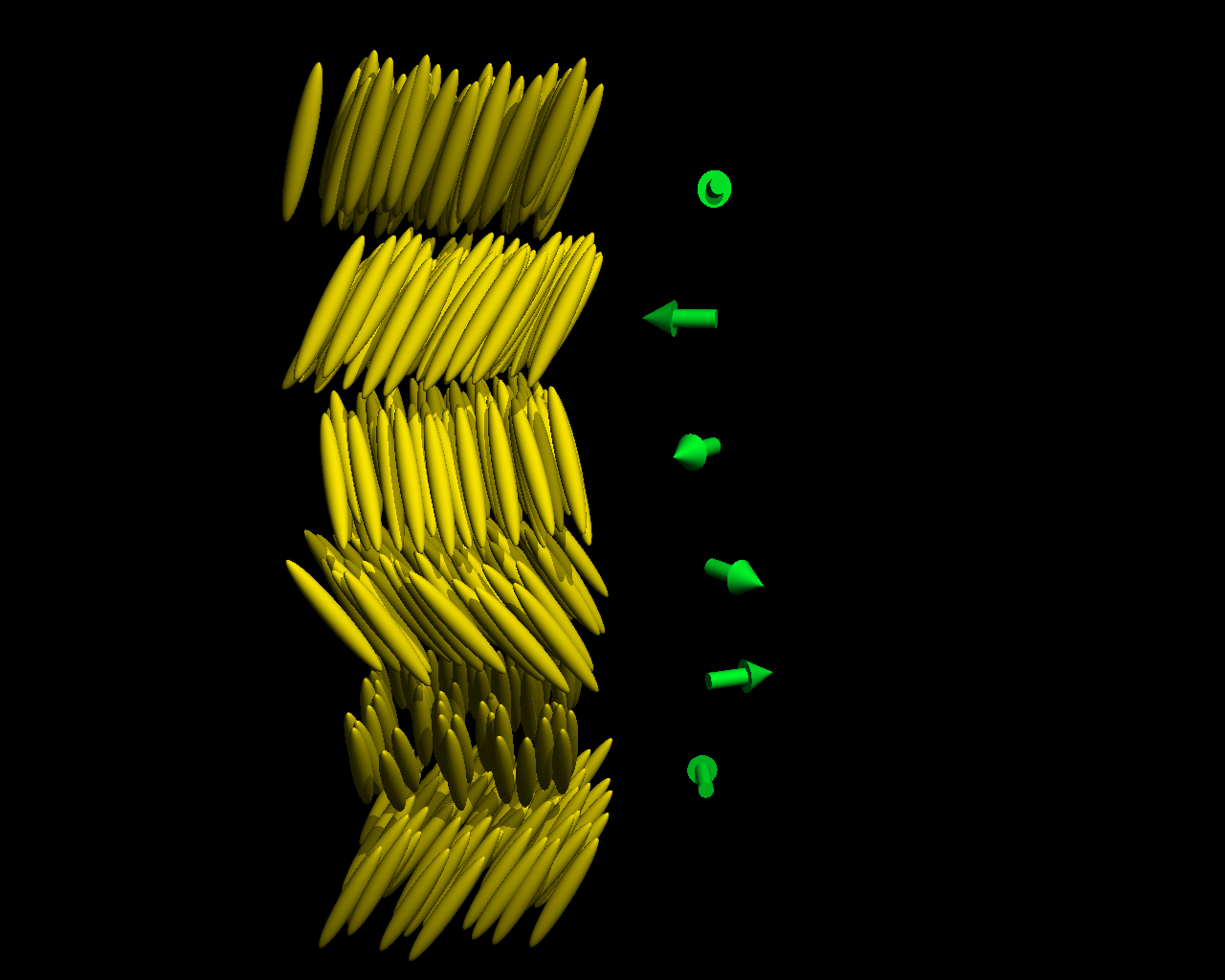
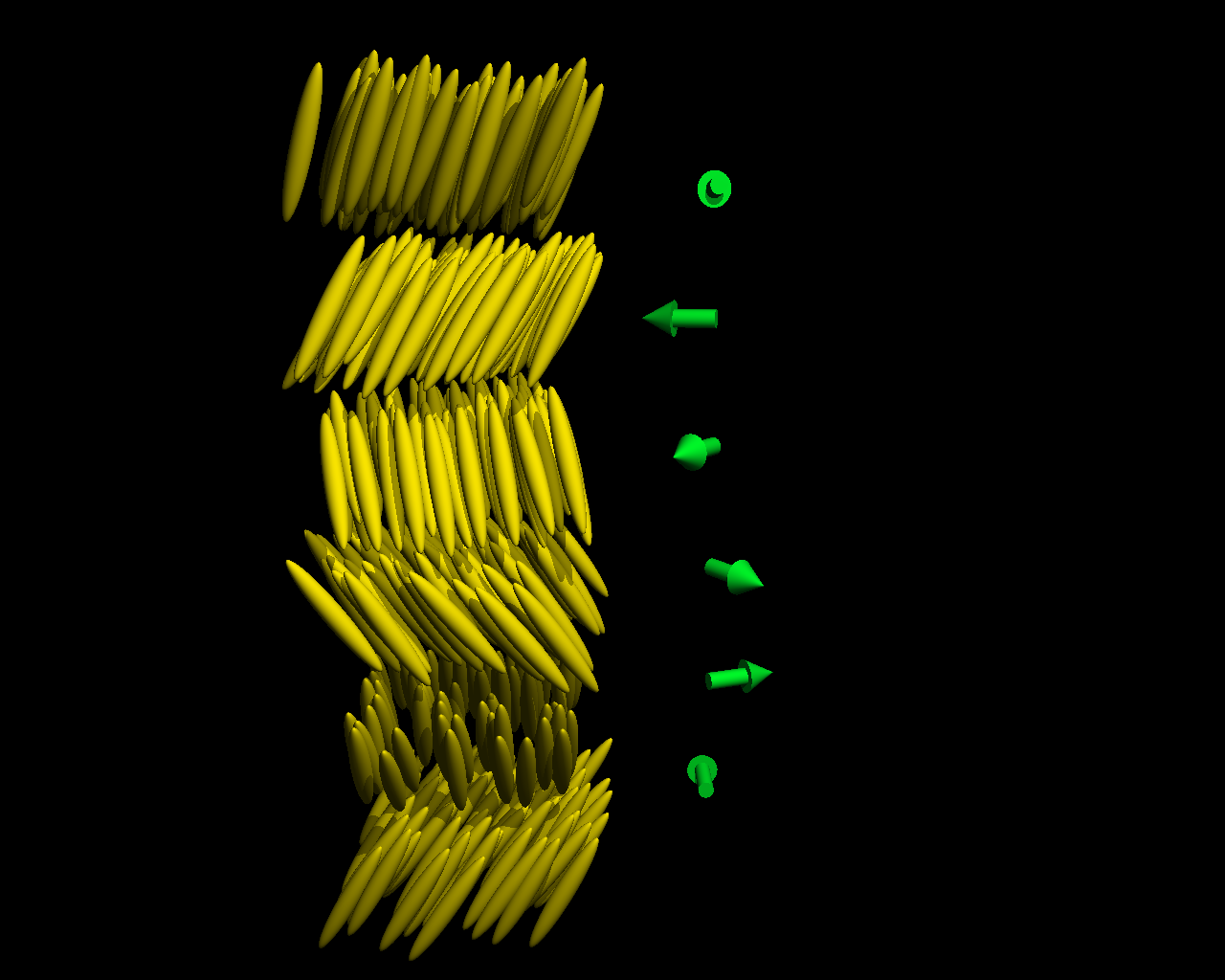
Finite size effects in liquid crystals
In the simplest magnets, neighboring spins prefer to line up parallel (a ferromagnet) or opposite to one another (an antiferromagnet), while in more complicated structures where ferromagnetic and antiferromagnetic interactions compete, the spins compromise and order into a helix.
This orderly pattern is destroyed, however, when the magnet is thinner than the helical pitch (that is, the number of lattice constants it takes for the spins to complete a rotation) [1]. Now, LiDong Pan, Shun Wang, and Cheng-Cher Huang at the University of Minnesota in the US and Chain-Shu Hsu at the National Chiao Tung University in Taiwan have looked at how molecular ordering in liquid crystals is modified by the same mechanism. Writing in Physical Review Letters, they present a systematic study of how film thickness alters the transition temperatures of five different phases in which the azimuthal angles of molecular tilts in adjacent layers vary in systematic ways.
Pan et al. determine the temperature at which the liquid crystal enters such so-called chiral smectic phases by studying the transmission of elliptically polarized light through the free-standing film. For most of the phases, they find that the transition temperature increases slightly in thinner films, but below a thickness of ten layers, a smectic phase with an approximately ten-layer pitch completely disappears and a smectic phase with a much longer pitch emerges.
Liquid crystals and helical magnets are not entirely analogous, particularly in how surface characteristics affect the order. However, the ordering in even very thin free-standing liquid-crystal films is accessible with optical techniques, whereas measuring the spin order in extremely thin magnetic films has been a challenge. Liquid crystals may therefore provide a complementary system with which to understand magnetism in reduced dimensions. – Jessica Thomas
[1] E. Weschke et al., Phys. Rev. Lett. 93, 157204 (2004).