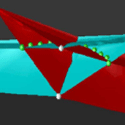
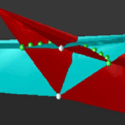
Dirac points multiply in the presence of a BEC
The ability to prepare ultracold atoms in graphenelike hexagonal optical lattices is expanding the types of systems in which Dirac dynamics can be observed. In such cold-atom systems, one could, in principle, study the interplay between superfluidity and Dirac physics. In a paper appearing in Physical Review Letters, Zhu Chen at the Chinese Academy of Sciences and Biao Wu of Peking University use mean-field theory to calculate the Bloch bands of a Bose-Einstein condensate confined to a hexagonal optical lattice.
The Dirac point is a point in the Brillouin zone around which the energy-momentum relation is linear. Its existence in graphene is at the heart of this material’s unusual properties, in which electrons behave as massless particles. Chen and Wu’s study predicts, surprisingly, that in the analog cold-atom system, the topological structure of the Dirac point is drastically modified: intersecting tubelike bands appear around the original Dirac point, giving rise to a set of new Dirac points that form a closed curve. More importantly, this transformation should occur even with an arbitrarily small interaction between the atoms, upending the idea that such topological effects can only occur in the presence of a finite interaction between atoms.
The modified band structure prevents an adiabatic evolution of a state across the Dirac point, violating the usual quantum rule that a system remains in its instantaneous eigenstate if an external perturbation is sufficiently slow. This effect could be tested experimentally in a so-called triple-well structure, which is a combination of rectangular and triangular optical lattices. – Hari Dahal