The end of the world at the Large Hadron Collider?
On 8 August, the Large Hadron Collider (LHC) at CERN injected its first beams, beginning an experimental program that will produce proton-proton collisions at an energy of . Particle physicists are waiting expectantly. The reason is that the Standard Model of strong, weak, and electromagnetic interactions, despite its many successes, is clearly incomplete. Theory says that the holes in the model should be filled by new physics in the energy region that will be studied by the LHC. Some candidate theories are simple quick fixes, but the most interesting ones involve new concepts of spacetime waiting to be discovered.
Look up the LHC on Wikipedia, however, and you will find considerable space devoted to safety concerns [1]. At the LHC, we will probe energies beyond those explored at any previous accelerator, and we hope to create particles that have never been observed. Couldn’t we, then, create particles that would actually be dangerous, for example, ones that would eat normal matter and eventually turn the earth into a blob of unpleasantness? It is morbid fun to speculate about such things, and candidates for such dangerous particles have been suggested. These suggestions have been analyzed in an article in Reviews of Modern Physics by Jaffe, Busza, Wilczek, and Sandweiss [2] and excluded on the basis of constraints from observation and from the known laws of physics. These conclusions have been upheld by subsequent studies conducted at CERN [3].
Nonetheless, there is one case that is especially subtle, the idea that the LHC will produce microscopic black holes that will grow to macroscopic size, slowly turning the whole earth into a black hole. Let me stress, first of all, that there is no actual theory that leads to this conclusion. You may judge this from the fact that my well-informed colleagues are all planning sabbaticals at CERN in Geneva, while none of them are moving to Melbourne. It is only after one makes a series of hypotheses about how our theories might be incorrect that a problem might appear. In a paper published in Physical Review D, Steven Giddings of the University of California at Santa Barbara, and Michelangelo Mangano of CERN, take these hypotheses as a challenge and use them as the basis for a new and fascinating investigation [4]. If all of these hypotheses are correct, they ask, wouldn’t the resulting black holes have already eaten something in the universe whose absence we would have noticed? They argue that well-known astrophysical objects would have been destroyed long ago if the LHC were able to produce dangerous black holes.
Why should the LHC, operating at energies of , produce strong quantum gravitational fields, which ordinarily would not be expected below the energy of the Planck scale ( )? The Standard Model of weak interactions includes spontaneous symmetry breaking and a symmetry violating ground state. The energy scale of this symmetry breaking is known to be of the order of . One of the questions about the Standard Model is the origin of this energy scale. Why could it not be as large as the Planck energy? In 1998, Arkani-Hamed, Dimopoulos, and Dvali (ADD) [5] turned this question on its head and asked whether the quantum gravity scale could be as small as a few hundred . They postulated that there are extra dimensions of space, such that gravity (curved space) can fill these dimensions, while quarks, leptons, photons, and other Standard Model particles are bound to a three-dimensional wall inside this space. Because the gravitational force increases more rapidly in higher dimensions, as in dimensions instead of , quantum gravity effects become strong at a larger distance or a lower energy.
Particle collisions at energies above the Planck scale must create black holes, because they put large amounts of energy within a small enough region (the so-called Schwarzschild radius). Giddings and Thomas [6] and Dimopoulos and Landsberg [7] realized that this logic, applied to the ADD model, implies that high-energy collisions at energies should produce black holes. They did not consider this a danger but rather an exciting possibility. They imagined that the black holes would glow with a temperature of about , emit large numbers of quarks, leptons, and bosons through Hawking radiation [8], and evaporate in . This process would produce unique and unmistakable events detectable by the LHC experiments.
But what if Hawking’s prediction that black holes emit radiation is incorrect? There is no direct evidence for Hawking radiation. The only black holes we have seen in nature are the size of stars or galaxies, and their Hawking radiation is invisible. With this hypothesis, the black holes predicted by the ADD model would be stable and might be captured by the earth, with dire consequences. Because we do not have a complete theory of quantum gravity, it is impossible to refute this speculation. However, the theoretical evidence for Hawking radiation is very strong. Numerous calculations from different points of view agree on the detailed formulae for the Hawking temperature and spectrum. A related effect, the Unruh effect [9] of radiation from an accelerated body, is demonstrable from quantum electrodynamics. Models have been proposed, including one by Unruh himself [10], in which black holes do not radiate. That model, however, requires violation of Lorentz invariance, which is plausible at but is completely excluded at energies.
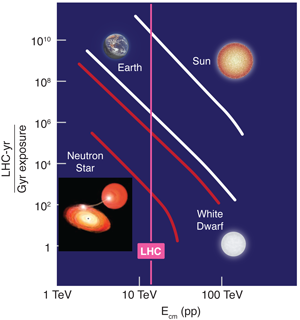
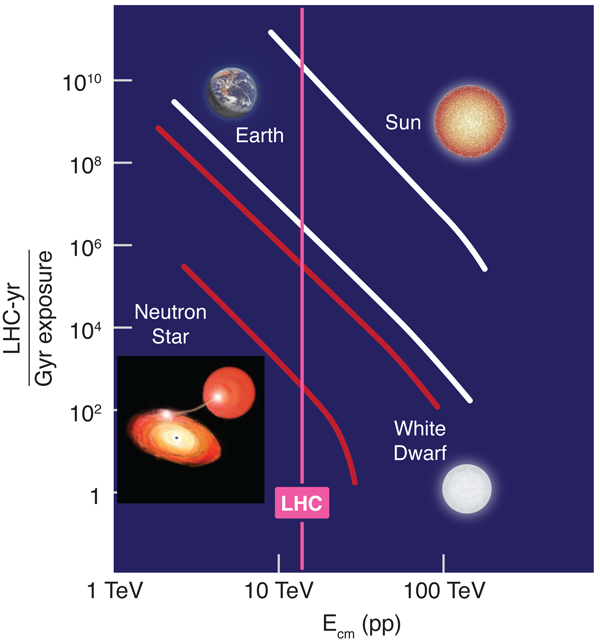
If we ignore these strong theoretical arguments, we could pursue another path. Huge numbers of high-energy cosmic rays have hit the earth over its lifetime. Thus, we can argue, nature has already carried out the LHC experiments many times. If we are still here, the LHC must be safe. This is a standard argument that was worked out carefully by Jaffe et al. [2]. Figure 1 shows the number of high-energy proton collisions above a given center-of-mass energy experienced by the earth and the sun per billion years as a result of cosmic-ray exposure. This argument is quite strong enough to exclude the dangers of any hypothetical particle that is captured by the earth. However, black holes might evade this argument. A structureless, neutral black hole in the ADD model has a radius one one-thousandth of the size of an atomic nucleus. Such a “slippery” black hole might be produced at the LHC and subsequently stop and lodge in the earth. However, such a black hole produced by cosmic rays would zoom through the earth at the speed of light, suffering in the process only a few glancing collisions. In this picture, the cosmic-ray argument seems to lose its force.
In the ADD model, most of the black holes produced at the LHC should not be slippery in this sense. The proton is a bound state. The elementary reactions at proton-proton colliders are the collisions of the individual constituent quarks and gluons. Black hole production, which requires the highest possible energies, will often result from quark-quark or quark-gluon collisions. These reactions produce black holes that carry electric charge and strong interactions. They will interact with matter like hadrons, and even relativistic ones will stop within a few tens of meters. It is possible that one of these black holes can pick up another quark, neutralize itself, and become slippery. The reaction of absorbing a quark is related [11] to the reaction in which a quark is emitted through Hawking radiation, so if there is no Hawking radiation, we expect no neutralization. But because we are speculating already, I will add the hypothesis that almost all black holes produced at the LHC are slippery ones.
Now we have a problem. To address it, Giddings and Mangano begin two new lines of analysis. First, instead of conventional objects such as the earth and moon, they consider the production of black holes on white dwarfs and neutron stars. These objects are denser than rock by factors of and , respectively, so even slippery black holes can stop and have a chance to do their damage. White dwarfs and neutron stars certainly exist in large numbers. The cooling of white dwarfs is well understood, and so the age can be inferred from the temperature. The age of a neutron star in an x-ray binary system, with mass flow from the companion into the neutron star, can be inferred from the radius and period of the system and the properties of the companion. There are many examples of each type of star that are more than a billion years old.
Second, Giddings and Mangano analyze with care the accretion of matter onto a microscopic black hole. The accretion rate depends on the details of the model of extra dimensions [12]. In some cases, black holes have only a tiny gravitational influence. A stopped black hole will eventually eat the earth atom by atom, but the process takes 100 billion years. In other cases of the ADD model, though, the stronger, extra-dimensional gravitational field can be felt at a radius that is large compared to the interatomic distance. Then a different, hydrodynamical, description must be used. Giddings and Mangano analyze this case using Bondi’s classical theory [13] and find that shorter accretion times, of the order of thousands of years, are possible. But the higher-density white dwarfs and neutron stars would be destroyed much more quickly by captured black holes. For white dwarfs, the accretion time is ten thousand times shorter. Neutron stars are so dense that they are already very close to the threshold for complete gravitational collapse. This implies that even a single microscopic black hole can catalyze the rapid collapse of the whole neutron star. However easy it might be to destroy the earth, these stars are much more vulnerable. Thus, superdense stars act as the proverbial canaries in the coal mine for black hole production at the LHC. As long as pulsars keep chirping, the earth is not in danger.
I emphasized at the beginning of this article that high-energy physicists are confident in the safety of the LHC, based on our understanding of physics at energies. It strengthens the argument to also be able to make use of our experience with high-energy cosmic rays. Such an appeal to experience is much easier for the general public to understand. However, as the figure indicates, the cosmic-ray energy spectrum falls steeply, so that we have little experience with cosmic-ray collisions at energies above . To justify higher-energy accelerators of the future, we will need to better engage the public in understanding the knowledge that we have gained from high-energy particles and in the fascination of our search for new laws of physics. I hope that both goals will be advanced by the exciting discoveries that will be made at the LHC.
Acknowledgments
I am grateful to Lance Dixon and Daniel Maitre for discussion of these issues. This work is supported by the Department of Energy under contract DE-AC02-76SF00515. However, the opinions expressed here are my responsibility alone.
References
- http://en.wikipedia.org/wiki/Safety_of_the_Large_Hadron_Collider
- R. L. Jaffe, W. Busza, F. Wilczek, and J. Sandweiss, Rev. Mod. Phys. 72, 1125 (2000)
- J. P. Blaizot et al., CERN report CERN.2003.001; J. Ellis et al., CERN report CERNPH.TH.2008.135, arXiv:0806.3414
- S. B. Giddings and M. L. Mangano, Phys. Rev. D 78, 035009 (2008)
- N. Arkani-Hamed, S. Dimopoulos, and G. Dvali, Physics Letters B 429, 263
- S. B. Giddings and S. Thomas, Phys. Rev. D 65, 056010 (2002)
- S. Dimopoulos and G. Landsberg, Phys. Rev. Lett. 87, 161602 (2001)
- S. W. Hawking, Commun. Math. Phys. 43, 199 (1975); 46, 206(E) (1976)
- W. G. Unruh, Phys. Rev. D 14, 870 (1976)
- W. G. Unruh and R. Schützhold, Phys. Rev. D 71, 024028 (2005)
- See, e.g., M. E. Peskin and D. R. Schroeder, An Introduction to Quantum Field Theory (Westview Press, 1995)[Amazon][WorldCat], section 5.4
- Although, for clarity, I discuss only the ADD model, Giddings and Mangano [4] analyze this issue in general models of TeV-scale gravity
- See, e.g., S. L. Shapiro and S. A. Teukolsky, Black Holes, White Dwarfs, and Neutron Stars (Wiley, 1983)[Amazon][WorldCat], section 14.3