Puzzling hot spots in the cosmic-ray sky
Almost a century following their discovery, cosmic rays—high-energy particles from outer space—continue to confront scientists with unexpected features. Cosmic rays constitute an important part of the energy budget of galaxies and they are also known for their extremes: the cosmic-ray flux covers a range of more than 32 orders of magnitude with energies that reach up to and beyond. Despite many important findings, the crucial questions remain unanswered: what and where are the sources of cosmic rays? The difficulty in solving this riddle is mostly due to the fact that cosmic rays (that is, the component that is not photons) do not point back to their source but are subject to strong deflections in cosmic magnetic fields. The multiple deflections effectively result in a diffusion process of cosmic rays in the galactic environment causing a high level of isotropy at earth. In particular, no point sources of cosmic rays should be visible at TeV energy scales, where a typical Larmor radius (the radius of the circular motion of a charged particles in a magnetic field) in the galactic disc is relatively small, only about 100 astronomical units.
This generally accepted and experimentally supported picture has now come into question owing to new data from a cosmic-ray detector experiment called Milagro [1]. In a paper in Physical Review Letters [2] the Milagro research team reports two localized regions of cosmic-ray excess and they discuss different scenarios to explain their observation. However, there is currently no compelling explanation for the hot spots, suggesting that it is time to take a fresh look at galactic cosmic-ray origins and propagation, including the effects of the interaction of the solar system with the interstellar medium (in the region called the heliosphere).
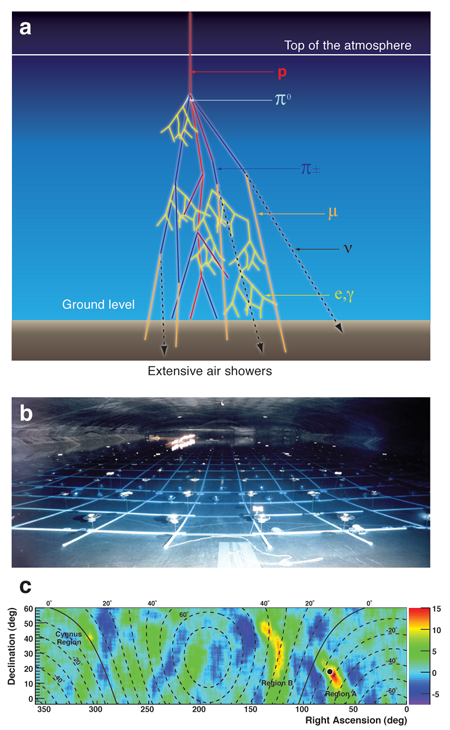
Milagro is a water Cherenkov air shower detector located in New Mexico (USA), above sea level [3]. Essentially, it is a six million gallon pond of surface area and in depth covered by a light-tight foil. More than 700 photomultiplier tubes arranged in a layer at the bottom and top each detect the faint Cherenkov light produced by charged particles from extensive air showers [see Figs. 1(a) and 1(b)]. A sparse array of smaller particle detector stations surrounds the pond and enables efficient separation between air showers initiated by photons and those created by hadrons.
The main purpose of Milagro is to study the gamma-ray sky in the TeV energy range. Other facilities, known as Imaging Atmospheric Cherenkov Telescopes (IACT), perform such studies very successfully and they reach a very high level of sensitivity to faint sources [4]. However, there are two disadvantages of such telescopes: Their small field of view requires pointing of the telescopes towards specific objects, and the observation of atmospheric Cherenkov light limits observations to clear moonless nights (~ 10% duty cycle). Instead, Milagro observes almost the entire sky above the horizon around the clock (90% duty cycle) but is limited by poorer directional resolution and worse gamma/hadron discrimination. Therefore, Milagro is complementary to IACT and ideally suited for full sky surveys.
In earlier studies, when searching for gamma-ray point sources or diffuse photon fluxes, the Milagro team applied strong selection rules to filter out photons from the hadron-induced air showers, which are about 1000 times more abundant. Now, in their new analysis, the cosmic-ray background rejection cuts were omitted, furnishing the experimenters with more than events collected during seven years of data-taking.
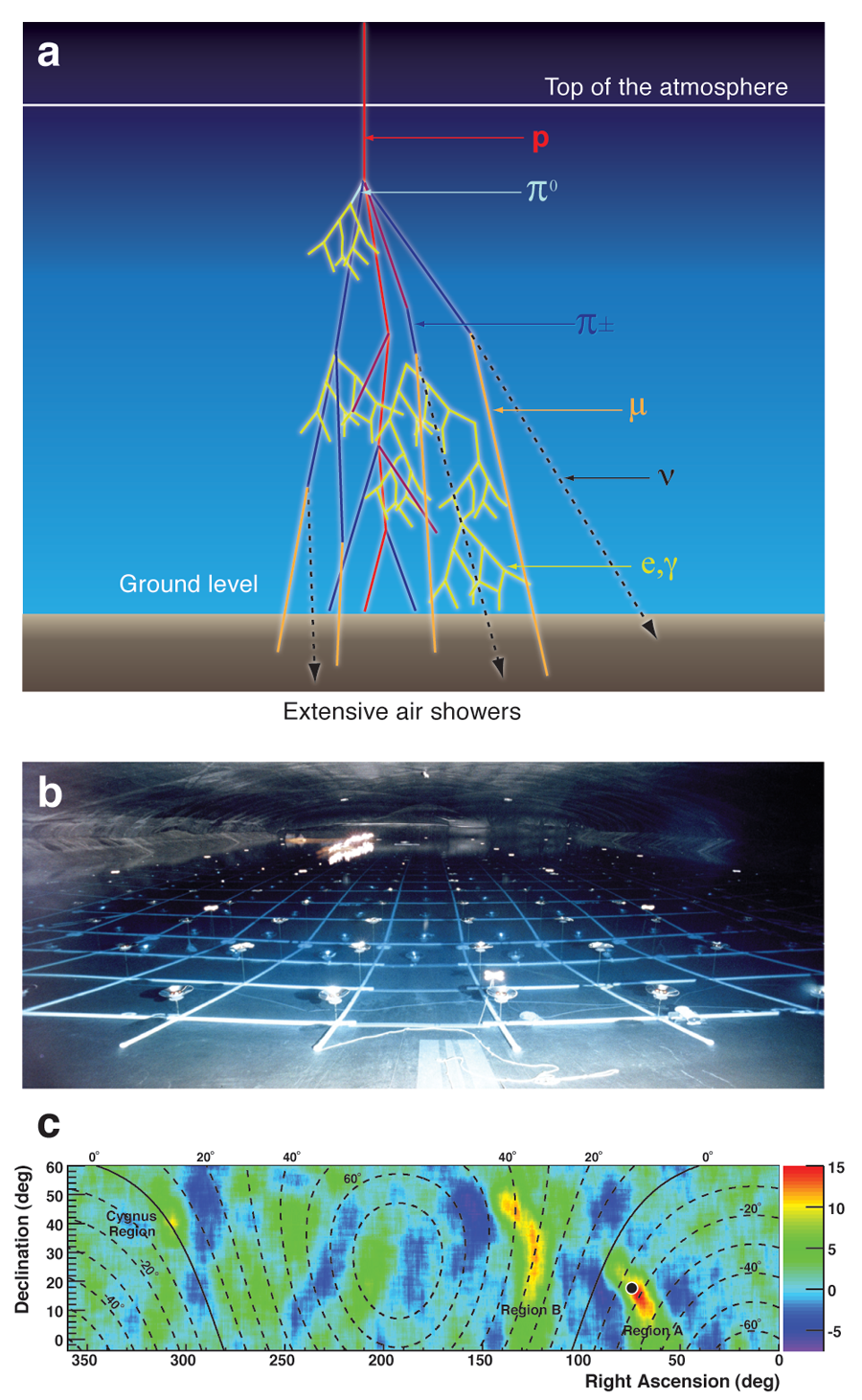
When generating a signal map from the arrival direction of the cosmic-ray enriched air showers, surprisingly, the researchers found two nearby regions of extended excesses [Fig. 1(c)] with peak significances of more than and with fractional excesses relative to the smooth cosmic-ray background of about . Potential systematic causes have been examined and excluded. (For technical reasons of precise background calculations, a 10° smoothing had to be applied to the signal map.) The excesses are found to be slightly stronger in winter than in summer, they are highly incompatible with pure gamma-ray emission, and the energy distributions in the excess regions appear harder (i.e., shifted to higher energy) than the background with peak emissions seen at about 10 TeV.
The incompatibility with photons leaves protons, neutrons, and nuclei as the messenger particles. Neutrons may be excluded, because their decay length at requires a source to be located within 0.1 parsecs, which is much less than the 1.3 parsec distance to the closest star beyond the solar system. If charged particles are involved, tracking them back to their origin means that even closer sources are required since the Larmor radius of a proton in the galactic disc (at a magnetic field of a few ) is only parsecs. Larger distances would become possible only if the magnetic field lines connect us to the source, but the hot spots do not seem to lie along what is thought to be the local interstellar field direction.
Some clues may come from the actual sky position of the hot spots [Fig. 1(c)]. The Milagro team noticed a directional coincidence of the stronger of the two hot spots with the heliotail. The heliotail is located in the direction opposite to the motion of the solar system with respect to the local interstellar medium (ISM), but there is no model of cosmic-ray acceleration in this region, so it may be purely coincidental. Drury and Aharonian [5] studied whether secondary neutron production in this gravitationally focused region of the ISM could account for the signal but they conclude that the required target density would need to be times the local density and thus should have been easily seen by astronomers studying the local bubble.
Salvati and Sacco [6] point out that the hot spots, which are separated from one another by an angle of about 50°, encompass the Geminga pulsar that resulted from a relatively young ( yrs) and nearby ( parsecs) supernova. The hypothesis that the hot spots are transient relics of the Geminga Supernova or, more generally, related to a nearby TeV acceleration mechanism is not implausible but cannot be proven yet. Also, it is questionable why the explosion resulted in such discrete localized features visible in cosmic rays.
Drury and Aharonian [5] propose a more general model based on leakage of particles through a magnetic trap from a local source. A magnetic-mirror field configuration between the trap and the solar neighborhood, assuming rather plausible parameters presumably associated with a nearby molecular cloud, could qualitatively describe all observed features. Again, this model is specifically constructed to explain the observations and further work is required to corroborate such an interpretation.
From the experimental point of view, we need independent data to confirm the Milagro results. The Tibet Air Shower Gamma Array experiment has collected even more data than Milagro and in fact they found some similarities in their sky-map [7]. In addition, they uncovered cosmic-ray anisotropies around the Cygnus region and found a corotation of galactic cosmic rays with the local galactic magnetic environment. Refining their analysis to verify the Milagro result is highly desirable. Moreover, studying the seasonal variation of the excess and comparison to underground muon data of Nagashima et al. [8] may shed some light on the question about the heliotail coincidence.
Important complementary insight into the puzzle may soon come from observations of high-energy cosmic-ray electrons. They undergo synchrotron and inverse Compton scattering losses and thus cannot travel very far from their sources, which makes them sensitive probes to nearby galactic sources and propagation. The Fermi Gamma-ray Space Telescope, formerly known as the Gamma-ray Large Area Space Telescope (GLAST), was successfully launched in June 2008 [9] and will deliver high-quality electron data in the relevant energy range from to . These data together with the aforementioned cross-checks to already existing cosmic-ray data will help to understand the very interesting hot spots and, more generally, will provide relevant answers to the origin and propagation of galactic cosmic rays. Answering the question about their origin before celebrating the 100 years anniversary of their discovery is an equally challenging and epoch-making task.
References
- http://www.lanl.gov/milagro/index.shtml
- A. A. Abdo et al., Phys. Rev. Lett. 101, 221101 (2008)
- R. Atkins et al., Astrophys. J. 595, 803 (2003)
- See, e.g., T. C. Weekes, astro-ph/0508253; W. Hofmann, astro-ph/0603076
- L. O’C. Drury and F. A. Aharonian, Astropart. Phys. 29, 420 (2008)
- M. Salvati and B. Sacco, arXiv:0802.2181
- M. Amenomori et al., Science 314, 439 (2006)
- K. Nagashima et al., J. Geophys. Res. 103, 429 (1998)
- http://fermi.gsfc.nasa.gov/acd/