Getting a better handle on nuclear matter at low density
Nuclear physicists rely on a phenomenological formula developed by Bethe and Weizsäcker to estimate the binding energy and thus mass of an atomic nucleus consisting of nucleons with neutrons and protons. This liquid-drop model formula tells us the following: (a) that uncharged symmetric nuclear matter (i.e., infinitely large with ) is bound by about per nucleon, (b) that infinite matter pays an energy penalty for being asymmetric in and , and (c) that finite real nuclei pay additional energy penalties for having a surface and for being charged. While the asymmetry penalty is, in principle, a function of density and temperature , as well as asymmetry, finite nuclei only inform us about this energy penalty near the saturation density ( , or somewhat less due to the surface), zero temperature, and near zero asymmetry [which is characterized by the variable ].
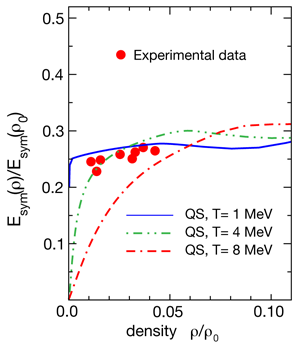
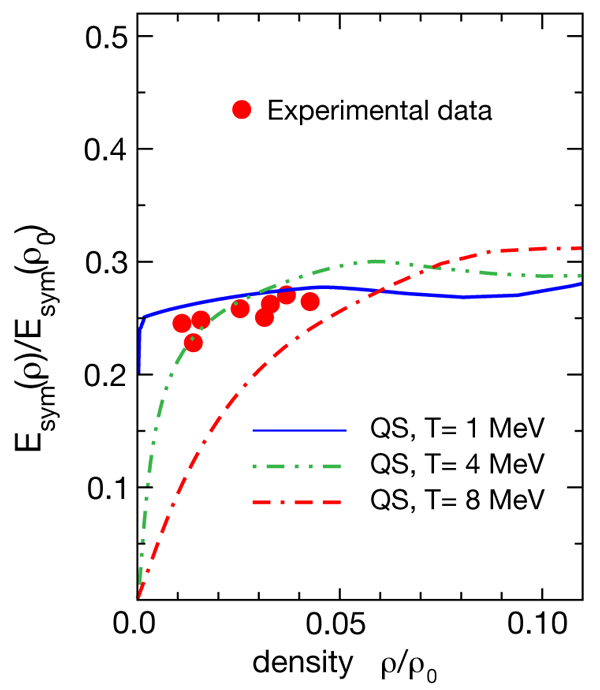
However, there are places in nature with densities ranging from much less (in objects such as you and I) to much greater than the saturation nuclear density, with asymmetries extending out to nearly (in neutron-stars) and temperatures that are significant on the nuclear scale (again in astrophysical sites). In the case of neutron stars, when calculating the total energy density of the matter resisting gravitational collapse, it is the asymmetry contribution that dominates the energy and thus the pressure. Now, Joseph Natowitz and colleagues at institutions in Germany, Italy, Poland, Russia, and the United States report in Physical Review Letters, a new approach [1] to extracting the density dependence of the asymmetry energy (at low density) that agrees with quantum statistical calculations (Fig. 1). This agreement provides some confidence that, for example, the pressure supplied by asymmetric matter (at low density) is understood.
The asymmetry energy [2] (which is a coefficient in the Bethe-Weizsäcker mass model multiplying a term, and thus generates a correction to the binding energy per nucleon) can be written in terms of the energy per nucleon as a function of the variables ( ) as,
From fitting nuclear masses, we know that .
Mean-field nuclear models can predict how the energy per nucleon varies with density, asymmetry, and temperature, but such models fall into a trap that van der Waals taught us to avoid—the assumption that matter is uniform. For example, the asymmetry penalty would go to zero as the density goes to zero only if the matter were uniform. However, at low density, even as low as our mean density, the asymmetry energy should be that of the nuclear clusters (i.e., nuclei) that compose matter. At low temperature, near-symmetric matter forms alpha-particle clusters. However, as the temperature increases, the additional phase space offered by dissolution of the clusters drives that outcome. On the other hand, as the density increases, clusters must melt (a Mott-type transition) into a nucleonic fluid. Understanding this inhomogeneous nuclear landscape in terms of the natural variables ( ) has been a vexing problem for decades.
Recent work, however, on both the experimental (using heavy-ion reactions) [1,3] and theoretical (quantum statistical [4] and virial [5]) fronts, has reached accordance in the description of the asymmetry energy when the density is a small fraction of the saturation density and the temperature is in the few range. This is a difficult (and thus interesting) region because the nonuniformity of the matter (i.e., the clusterization) is evolving.
On the experimental front, the asymmetry contribution to the free energy has been obtained for densities in the range and temperatures . This is done by comparing the yield of fragments ), with neutron number and charge , produced from two reacting systems of different overall asymmetries (designated by the subscript ) and by assuming these yields are determined by standard equilibrium expressions. Thus from experiments, similar except that the overall asymmetries are different, two “isoscaling” parameters ( and ), characterizing the difference in the fragment yields between the two experiments, are extracted [6],
These yields, assuming equilibrium (in this case at constant temperature and volume [7]), yields the expectation that , where is the free energy of a cluster of neutron number and proton number , and the are the nucleon chemical potentials.
With the use of a liquid-drop model expansion for the free energy, the fragment yield isoscaling parameters pick out the asymmetry energy terms, (i.e., only these terms can make the yields of a given ( ) fragment different in experiments differing principally in overall asymmetry). Reasonable expressions can be constructed for the isoscaling parameters in terms of , , , and . Thus the experimental determination of say , provides an estimate of the asymmetry component of the free energy at the values of the thermodynamic state variables of relevance when the fragments were created.
These thermodynamic state variables themselves are calculated within the same local equilibrium assumptions. First, the temperature is determined by employing ( and ) isotope yields in a Boltzmann logic (i.e., the ratio of yields are given by the differences in binding energy over the with spin effects included by corrective factors). Second, the relevant asymmetry (of the material producing the fragments) is measured from the yield of neutrons and protons bound in fragments supplemented by the free proton and neutron densities. The latter are calculated by assuming and equilibria. The equilibria imply that the free proton and neutron densities are derivable from simple phase-space considerations. For example, the equilibrium constant ( ) from which the neutron density ( ) can be extracted is
where the partition function factors coming from translation (an extra particle moving in ) and binding, have been separated out. (The densities are extracted from the above, as once is known, using the isotope yield thermometer, all is known in the above expression except for the nucleon densities.)
Natowitz et al. then call upon theory to extract the asymmetry energy from the asymmetry free energy. This amounts to accounting for the entropy of free nucleons, the trivial entropy of mixing, and the entropy lost when clusters are formed. As the entropy of mixing is maximal at symmetry (a concave downward function, , where are the composition fractions), the asymmetry entropy (the entropy change with increasing asymmetry) would normally be negative. However, at low , the clustering (predominately alphas) is suppressed with increasing asymmetry, enhancing the entropy (with increasing asymmetry). The authors of the paper use a nuclear statistical equilibrium (NSE) model for this purpose.
To verify that the low-density asymmetric matter is well understood, Natowitz et al. use the touchstone of comparing the extracted asymmetry energy to that predicted by a model based on a generalized Bethe-Uhlenbeck expansion [4]. The asymmetry energies from this approach are compared to those extracted from experiment (Fig. 1). This model accounts for the formation of clusters with decreasing density and their reduced binding and ultimate melting with both increasing density and temperature. The agreement between the experimentally derived (but NSE assisted) asymmetry energies and the many-body theory (see Fig. 1) provides confidence that the asymmetry energy, at low density, is understood. Specifically, the asymmetry energy does not go to zero at low density, as would be expected for uniform nucleonic matter, but rather saturates at a value close to . This plateau will persist at lower temperatures (as the clusters will be retained at even lower temperatures) but the plateau will break, with going to , at high temperature when the clusters melt.
The recent work discussed here gives us confidence that we now understand very low density (an order of magnitude less than saturation) asymmetric nuclear matter. Future work at the newly approved Facility for Rare Isotope Beams (FRIB) to be operated by Michigan State University will be directed at generating similar confidence for asymmetric matter at higher densities.
References
- J. B. Natowitz, G. Röpke , S. Typel, D. Blaschke, A. Bonasera, K. Hagel, T. Klähn , S. Kowalski, L. Qin, S. Shlomo, R. Wada, and H. H. Wolter, Phys. Rev. Lett. 104, 202501 (2010)
- Most of the literature calls this the “symmetry” energy. I prefer the “asymmetry” energy as it is the energy cost of generating an asymmetry, i.e., this energy is zero at zero asymmetry
- S. Kowalski et al., Phys. Rev. C 75, 014601 (2007)
- S. Typel et al., Phys. Rev. C 81, 015803 (2010)
- C. J. Horowitz and A. Schwenk, Nucl. Phys. A 776, 55 (2006)
- A. Ono et al., Phys. Rev. C 68, 05160 (2003)
- The Helmholtz free energy (F) is assumed to the relevant free energy for fragment production in the work of Natowitz et al. However, neither volume nor pressure can be considered as fixed. Therefore the experimentally extracted quantity is likely something between F and the Gibbs free energy G and the quantity ultimately deduced is something between an internal energy and an enthalpy H