New horizons for Hawking radiation
In 1974, Steven Hawking predicted that black holes were not completely black, but were actually weak emitters of blackbody radiation generated close to the event horizon—the boundary where light is forever trapped by the black hole’s gravitational pull [1]. Hawking’s insight was to realize how the presence of the horizon could separate virtual photon pairs (constantly being created from the quantum vacuum) such that while one was sucked in, the other could escape, causing the black hole to lose energy. Hawking’s idea was significant in suggesting a possible optical signature of a black hole’s existence. Yet, even though the prediction created an extensive theoretical literature in cosmology, calculations have since shown that Hawking radiation from black holes is so weak that it would be practically impossible to measure.
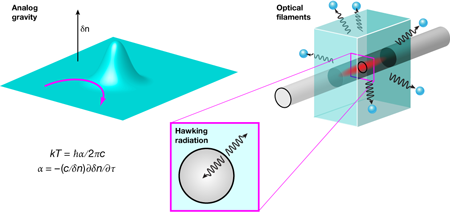
It turns out, however, that the physics of how waves interact with a horizon does not depend in a fundamental way on the presence of gravity at all. In principle, an analogous Hawking radiation should occur in other systems [2,3]. The key requirement is simply that the interaction between waves and the medium in which they propagate causes there to be a boundary between zones where the wave and the medium have different velocities [4,5]. In a paper in Physical Review Letters [6], Francesco Belgiorno at the Università degli Studi di Milano, in collaboration with researchers at several other institutes, also in Italy, describe a series of experiments where high-intensity filaments of light in glass perturb the optical propagation environment in an analogous manner to the way a gravitational field affects light near a black hole horizon. This perturbation creates the optical equivalent of an event horizon that allows Belgiorno et al. to make convincing measurements of analog Hawking radiation at optical frequencies [7]. These results are highly significant in suggesting a system in which Hawking’s prediction can be fully explored in a convenient laboratory environment.
A really useful way to visualize an analog event horizon is to imagine a fish swimming upstream in a river flowing towards a waterfall [4,5]. The point at which the current flows faster than the fish can swim represents a boundary at which fish cannot escape and they are swept over the waterfall. This “point of no return” for the fish is equivalent to a black hole horizon. A similar analogy exists for white holes, associated with horizons that fish can never enter, namely, if they were attempting to swim upstream towards the bottom of a waterfall. This simple picture is surprisingly powerful at capturing the physics of horizons, and can be extended rigorously to describe horizon physics in diverse systems including acoustics, cold atoms, and gravity-capillary waves on water [8–11]. Indeed, horizon effects and a stimulated form of Hawking radiation have recently been explicitly observed in the vicinity of an obstacle placed in an open channel flow [12]. However, the question has remained open as to whether these analog gravity systems also generate the spontaneous thermal radiation Hawking predicted.
Belgiorno et al.’s experiments suggest that the answer is yes. They created an optical event horizon by using intense, ultrashort light pulses that change the refractive index of the glass in the vicinity of the moving pulse [13]. The change in the refractive index modifies the effective propagation “geometry” (Fig. 1, left) as seen by copropagating light rays such that a trapping horizon forms and, in principle, Hawking radiation should occur. The changing index is an effect called a Kerr nonlinearity, whereby a pulse modifies the refractive index of glass such that it is higher at the center of the pulse than the wings. Because wave speed depends on refractive index, the propagating pulse induces an effective velocity gradient in the material such that horizons can appear at points on the pulse leading and trailing edges.
It is important to note here that Kerr-induced trapping in itself is not a new effect, but rather one that is well known in nonlinear fiber optics [14–16]. In fact, the Raman frequency shifting on solitons (where the spectrum of short pulses moves to longer wavelengths) is a deceleration effect that was even shown to lead to an equivalent gravitational potential [16,17], but it was only recently that scientists appreciated the possibility of extending the gravitational analogy to test predictions of Hawking radiation [13]. The particular attraction of experiments in optics is that the intensity and wavelength of the Hawking radiation depends on the induced refractive index gradient, and pulses containing only a few optical cycles or a steep shock front would be expected to generate measureable emission of visible light. Unfortunately, although it is straightforward to demonstrate the existence of an event horizon in an optical fiber [13], dispersive and dissipative effects present in the fiber appear to prevent the clean formation of the particular pulse profiles needed for the spontaneous generation of Hawking radiation.
The experiments of Belgiorno and co-workers attempt to overcome this problem in a novel way. In fact, they move away from the fiber environment altogether, performing experiments in bulk glass, using laser pulses in the form of needlelike beams known as optical filaments (Fig. 1, right) to generate the nonlinear refractive index perturbation [18]. Optical filament pulses generally have a complex spatiotemporal structure, but it is possible to experimentally synthesize them so that their internal group and phase velocity gradients can be controlled. This is what Belgiorno et al. did in their experiments, using properties of what are called Bessel beams, where the filament is preshaped so as to control its group velocity relative to the velocity change induced by the refractive index perturbation. This is a crucial aspect of their experiments because it allows them to fine tune the window of Hawking radiation emission into the near infrared, around away from any other possible contaminating signals. With a cooled CCD camera, they detect a clear signal above background that they associate with Hawking radiation, and the spectral shift of this signal with incident energy is in good agreement with the predictions of theory. They also performed experiments where the filaments were formed from Gaussian pulses, and although the dynamics are more complicated here, the spectral emission window of the spontaneous radiation is again in agreement with theory.
Overall, this work provides significant evidence for the observation of Hawking radiation in an analog gravity system. The results must nevertheless be interpreted carefully. For example, it is essential to state very plainly that measuring analog Hawking radiation gives no direct insight into quantum gravity because there is no physical gravitational potential involved. Indeed, one might even argue that the description of this emission as “Hawking” radiation is inappropriate, but this seems an unnecessary restriction because the study of analog horizon systems was clearly motivated by Hawking’s work over years ago. Of course additional experiments still remain to be carried out. Specifically, the spontaneous photon pairs emitted on either side of the horizon may be detectable with suitable angular resolution [18], and measurements of their entanglement and correlation will be an essential next step. Moreover, the polarization properties of filaments are very subtle and may need to be taken into account more fully in a complete interpretation of the experiments.
This field of research is at the interface of several areas of physics, and “standardizing” the terminology would be welcome. For example, effects related to Cerenkov radiation are seen both in filament and fiber soliton propagation [15,16], and distinguishing similarities and differences is important to avoid confusion. On the other hand, Belgiorno et al.’s results now point out the clear need to study the quantum electrodynamics of soliton radiation, as this may have direct bearing on their experiments. This work is also likely to be far reaching in other ways. By showing how tailored spatiotemporal fields provide a high degree of control over the interaction geometry of propagating light pulses, they may represent a new example of experiments in “ultrafast transformation optics,” where geometrical modifications of an optical propagation environment can be induced on ultrafast timescales. This may allow a much wider study of other analog physical effects, using a convenient benchtop platform.
Corrections (6 December 2010): Paragraph 3, sentence 5, “capillary waves” changed to “gravity-capillary waves.” References 2, 3, 10, 13 and 18, changed/updated.
References
- S. W. Hawking, Nature 248, 30 (1974)
- W. G. Unruh, Phys. Rev. Lett. 46, 1351 (1981)
- P. C. W. Davies and S. A. Fulling, Proc. R. Soc. London A 356, 237 (1977); M. Visser, Classical Quantum Gravity 15, 1767 (1998)
- U. Leonhardt and T. G. Philbin, Philos. Trans. R. Soc. A 366, 2851 (2008)
- W. G. Unruh, Philos. Trans. R. Soc. A 366, 2905 (2008)
- F. Belgiorno, S. L. Cacciatori, M. Clerici, V. Gorini, G. Ortenzi, L. Rizzi, E. Rubino, V. G. Sala, and D. Faccio, Phys. Rev. Lett. 105, 203901 (2010)
- D. Faccio, S. Cacciatori, V. Gorini, V. G. Sala, A. Averchi, A. Lotti, M. Kolesik, and J. V. Moloney, Europhys. Lett. 89, 34004 (2010)
- P. Ball, Nature 411628 (2001)
- Artificial Black Holes, edited by M. Novello, M. Visser, and G. E. Volovik (World Scientific, Singapore, 2002)[Amazon][WorldCat]
- G. Rousseaux, C. Mathis, P. Maïssa, T. G. Philbin, and U. Leonhardt, New J. Phys. 10,053015 (2008); R. Schützhold and W. G. Unruh, Phys. Rev. D 66, 044019 (2002)
- G. Rousseaux, P. Maïssa, C. Mathis, P. Coullet, T. G. Philbin, and U. Leonhardt, New J. Phys. 12,095018 (2010)
- S. Weinfurtner et al., Phys. Rev. Lett. (to be published); arXiv:1008.1911v2 (gr-qc)
- T. G. Philbin, C. Kuklewicz, S. Robertson, S. Hill, F. König, and U. Leonhardt, Science 319, 1367 (2008); R. Schützhold and W. G. Unruh, Phys. Rev. Lett. 95, 031301 (2005)
- N. Nishizawa and T. Goto, Opt. Express 10, 1151 (2002)
- J. M. Dudley, G. Genty, and S. Coen, Rev. Mod. Phys. 78, 1135 (2006)
- D. V. Skryabin and A. V. Gorbach, Rev. Mod. Phys. 82, 1287 (2010)
- A. V. Gorbach and D. V. Skryabin, Nature Photon. 1, 653 (2007)
- F. Belgiorno, S. L. Cacciatori, G. Ortenzi, V. G. Sala, and D. Faccio, Phys. Rev. Lett., 104,140403 (2010)