Charge Hopping in Glassy Magnets

Gavin Lawes

Viewpoint

Charge Hopping in Glassy Magnets

Department of Physics and Astronomy, Wayne State University, Detroit, MI 48201, USA

March 19, 2012• Physics 5, 35

In some transition metal oxides, disorder makes the dielectric constant highly sensitive to an applied magnetic field over a broad range of temperatures.

Figure caption — **Figure 1:** Schematic illustration of the mechanism for magnetodielectric coupling in partially antisite-disordered ${La}_{2} {NiMnO}_{6}$ . Green: $La$ ; Blue: $Ni$ ; Red: $Mn$ ; Gray: Bridging $O$ . The gray arrows on the O ions represent the magnetic interactions between neighboring magnetic ions. Charge transfer between the ${Ni}^{2 +}$ and ${Mn}^{4 +}$ produces a large dipole moment in the unit cell, which is suppressed by the ferromagnetic spin alignment in an applied magnetic field.

Magnetodielectric materials, which have a dielectric constant that is modulated by an applied magnetic field, provide rich insight into the physics of spin-charge coupling. The coupling between the dielectric constant and magnetic field—the magnetodieletric coupling—is often mediated by lattice dynamics [1], typically leading to only very small shifts in the dielectric constant. Some special classes of materials do exhibit exceptionally large shifts—a relative change in the dielectric constant of $500 %$ in high magnetic fields [2]—but these effects are generally present only in a very narrow range of temperatures near a phase transition and are not suitable for robust device applications. Materials having a substantial magnetodielectric coupling at high temperatures are expected to lead to the development of novel devices, including capacitive magnetic field sensors and tunable high-frequency filters [3,4]. One of the outstanding challenges in the study of magnetodiectrics is to identify mechanisms that can lead to strong spin-charge coupling, with the goal of producing large magnetically induced shifts in the dielectric response over a wide temperature range encompassing room temperature.

In a paper appearing in Physical Review Letters [5], Debraj Choudhury at the Indian Institute of Science, Bangalore, and coauthors propose a design for materials with strong magnetodielectric coupling based on tuning the spin-dependent electron hopping in site-disordered crystals. Their experimental and theoretical investigation on the magnetic and electrical properties of partially disordered ${La}_{2} {NiMnO}_{6}$ has produced the unexpected result that the spatial arrangement of the transition metal ions leads to large magnetodielectric coupling over a broad temperature range.

The authors considered the effects of chemical disorder—central to the work—on magnetodielectric coupling in the double perovskite ${La}_{2} {NiMnO}_{6}$ . X-ray absorption spectroscopy measurements indicate that the nickel ( $Ni$ ) and manganese ( $Mn$ ) ions are present in the $2 +$ and $4 +$ valence states, respectively. Previous work on disorder-free ${La}_{2} {NiMnO}_{6}$ had established that the ${Ni}^{2 +} - O - {Mn}^{4 +}$ magnetic interactions are ferromagnetic [6]. When the ${Ni}^{2 +}$ and ${Mn}^{4 +}$ ions switch positions, referred to as antisite disorder, ${Mn}^{4 +} - O - {Mn}^{4 +}$ and ${Ni}^{2 +} - O - {Ni}^{2 +}$ additional magnetic interactions are formed in the system. These exchange interactions are antiferromagnetic and therefore reduce the saturation moment per unit cell of the sample; the measured moment indicates the presence of approximately $20 %$ antisite disorder.

The antisite disorder modifies the temperature-dependent magnetic properties of ${La}_{2} {NiMnO}_{6}$ . Both disorder-free and disordered ${La}_{2} {NiMnO}_{6}$ exhibit a ferromagnetic transition near $270 K$ [6,7]. In addition, the authors find strong evidence for a spin-glass-like phase developing at lower temperatures in the disordered sample, which they attribute to frustration arising from the competition between the ferromagnetic and disorder-induced antiferromagnetic interactions. The phase has a dramatic effect on the magnetodielectric coupling.

The antisite disorder also has important ramifications for the electrical properties of the system. Because dielectric measurements are often dominated by effects arising from charge accumulation near electrodes or grain boundaries [7], the authors first carefully separated these extrinsic contributions from the intrinsic behavior of disordered ${La}_{2} {NiMnO}_{6}$ . Detailed analysis of the frequency-dependent dielectric measurements established that the capacitive response arose from two contributions, a relaxation term that dominates at low frequencies and one suitable for noninteracting dipoles (the Debye term) that becomes relevant at higher frequencies. The Debye component may be associated with the hopping of charge carriers between ${Ni}^{2 +}$ and ${Mn}^{4 +}$ sites, and can lead to the large dielectric constant of disordered ${La}_{2} {NiMnO}_{6}$ , which is found to be significantly larger than that measured in disorder-free ${La}_{2} {NiMnO}_{6}$ [6].

Most significantly, the authors observed that the dielectric constant of antisite-disordered ${La}_{2} {NiMnO}_{6}$ has a strong dependence on magnetic field over a wide temperature range. Large magnetodielectric shifts are observed from temperatures as low as $100 K$ , associated with the development of the glassy state, to room temperature, where the magnitude of the shift reaches $16 %$ . This work complements an earlier study on disorder-free ${La}_{2} {NiMnO}_{6}$ , which also found similar magnetodielectric shifts but over a smaller range of temperatures [6]. The large magnetic-field-induced shift in the capacitance of the disordered ${La}_{2} {NiMnO}_{6}$ cannot be readily attributed to extrinsic effects. While charge accumulation at grain boundaries or electrodes combined with magnetoresistive effects can cause a similar magnetocapacitive shift [8], the ${La}_{2} {NiMnO}_{6}$ sample in this study shows only a small magnetoresistance (less than $0.3 %$ ).

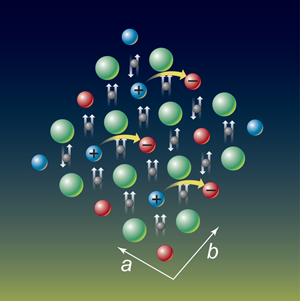
To explain their observations, the authors propose a model in which the large magnetodielectric coupling is produced by asymmetric charge hopping between the transition metal sites. This model is schematically illustrated in Fig. 1. In the presence of an electric field, electrons will hop between the ${Ni}^{2 +}$ and ${Mn}^{4 +}$ ions to produce a charge-transferred state with ${Ni}^{2 + δ}$ and ${Mn}^{4 - δ}$ . This introduces a large dipole moment through the unit cell, yielding the relaxation observed in the dielectric measurements. This hopping is enhanced by the antisite disorder in the system, which introduces midgap states associated with local deviations from the ferromagnetic order. The application of a large magnetic field reduces the concentration of these states, which is argued to produce the experimentally observed reduction in the dielectric constant. The authors make a case for a strong interplay between the magnetic properties and disorder in ${La}_{2} {NiMnO}_{6}$ with first-principles calculations, which show that a ferrimagnetic state is stabilized, relative to the ferromagnetic structure, by antisite disorder.

This work, taken together with earlier studies on disorder-free ${La}_{2} {NiMnO}_{6}$ [6], demonstrates the important role played by disorder in the coupling between spin and charge, and offers a mechanism for introducing large magnetodielectric shifts in insulating magnetic systems. While the study focuses on ${La}_{2} {NiMnO}_{6}$ , the conceptual framework for this behavior may be translated to other antisite-disordered dielectric magnets. Experimental specifics, however, may prove challenging. The dielectric response is sensitive to extrinsic effects and charge accumulation. The introduction of disorder in other systems may increase the leakage current, limiting the suitability for dielectric applications. More fundamentally, dielectric ferromagnets are relatively rare, and it is not clear whether the very dramatic magnetodielectric effects observed in ${La}_{2} {NiMnO}_{6}$ associated with charge transfer will persist in other types of magnetic materials that have different spin arrangements. Despite these challenges, the mechanism for charge-hopping-mediated magnetodielectric effects presented in this Letter offers a new angle for exploring a fascinating and important instance of spin-charge coupling in insulating magnets.

References

G. Lawes, A. P. Ramirez, C. M. Varma, and M. A. Subramanian, Phys. Rev. Lett. 91, 257208 (2003)
T. Goto, T. Kimura, G. Lawes, A. P. Ramirez, and Y. Tokura, Phys. Rev. Lett. 92, 257201 (2004)
Y.P. Yao, Y. Hou, S.N. Dong, and X.G. Li, J. Appl. Phys. 110, 014508 (2011)
K. Garello, E. Benevent, J. P. Michel, D. Cros, and B. Viala, IEEE Trans. Magn. 45, 4325 (2009)
D. Choudhury, P. Mandal, R. Mathieu, A. Hazarika, S. Rajan, A. Sundaresan, U. V. Waghmare, R. Knut, O. Karis, P. Nordblad, and D. D. Sarma, Phys. Rev. Lett. 108, 127201 (2012)
N. S. Rogado, J. Li, A. W. Sleight, and M. A. Subramanian, Adv. Mat. 17, 2225 (2005)
P. Thongbai, S. Pongha, T. Yamwong, and S. Maensiri, Appl. Phys. Lett. 94, 022908 (2009)
G. Catalan, Appl. Phys. Lett. 88, 102902 (2006)

About the Author

Gavin Lawes is an associate professor of physics at Wayne State University. He received his Ph.D. from Cornell University in 2001, which was followed by a postdoctoral position at Los Alamos National Laboratory. He joined the faculty of the Department of Physics and Astronomy at Wayne State University as an assistant professor in 2004. His research interests are focused on novel magnetic materials, including magnetoelectrics and multiferroics, magnetic nanoparticles, and magnetic semiconductors.