The Twists and Turns of the Dynamo Effect
Magnetic fields are ubiquitous in the universe. The Earth has a magnetic field that turns a magnetic needle into a useful navigational tool. Other planets, the Sun, and most stars generate their own magnetic fields. It is commonly accepted that most celestial bodies maintain magnetic fields through the dynamo effect: conversion of the kinetic energy of an electrically conducting, but electrically neutral, fluid or plasma into magnetic energy. Writing in Physical Review Letters, Basile Gallet at the Ecole Normale Supérieure in Paris, France, and colleagues report their observations of localized magnetic fields in a laboratory device [1], reproducing for the first time a key feature of astrophysical and planetary dynamos.
Until the late 1950s, researchers doubted whether a dynamo in a homogeneous conducting medium could exist, but the basic physics of dynamos is relatively straightforward. Fluid motions of the appropriate shape stretch magnetic field lines and amplify preexisting magnetic fields, provided that the field amplification through stretching occurs faster than the energy loss through ohmic dissipation. The ratio of stretching over diffusion is quantified by the magnetic Reynolds number, a dimensionless number analogous to the Reynolds number familiar from hydrodynamics in which the kinematic viscosity is replaced with the magnetic diffusion. Fluid flows at equal Reynolds numbers are identical to each other up to scale factors. That is why the flow around an airplane wing can be studied by placing downscaled models of a wing into a wind tunnel. In the same fashion, magnetohydrodynamic flows are identical at equal magnetic Reynolds numbers and a laboratory size apparatus can reproduce the functioning of a planetary core.
The dynamo effect has been simulated numerically many times by solving the Navier-Stokes equation coupled to the induction equation (a reduction of Maxwell’s equations, valid if the fluid velocity is small compared with the speed of light and if Ohm’s law applies). However, dynamos in nature are turbulent, so that realistic simulations face the same difficulties as, for example, simulations of the flow around an airplane wing. Ab initio computations of those flows require computational resources that are unavailable at present.
Just as in any computer modeling, dynamo simulations have to be supplemented with experiments. The experiments are technically demanding because they need to operate at magnetic Reynolds numbers large enough for magnetic fields to self-generate. This typically requires volumes of several cubic meters of liquid sodium moving at velocities of several meters per second. The merit of the first successful dynamo experiments [2,3] was first and foremost to break the barrier of the critical magnetic Reynolds number. No experiment can reproduce all features of a planetary or stellar dynamo on a laboratory scale and second-generation experiments are designed to elucidate particular aspects of the dynamo effect. It is interesting from this perspective to compare a recent survey of experiments [4] with a review that appeared just before the first experiments were successful [5].
Gallet et al. [1] have found a way to push the envelope of dynamo experiments by studying the puzzling phenomenon of localized fields. Even though it cannot be verified by present day direct observation, it is possible that the Sun had a magnetic field of this type during the so called Maunder minimum, the period from 1645 to 1715 during which the Sun had few sunspots, and those which existed appeared on only one hemisphere, suggesting a magnetic field confined to one hemisphere. It is often pointed out that this period coincides with the “Little Ice Age,” a period of low average temperatures in Europe and North America, but it is debated whether there is a causal relation between the two. Mars has no working dynamo nowadays, but its surface magnetization suggests that until billion years ago, Mars was also the seat of a dynamo localized in a single hemisphere. There are also numerical simulations of hemispherical dynamos.
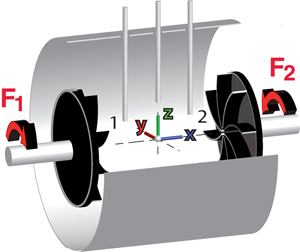
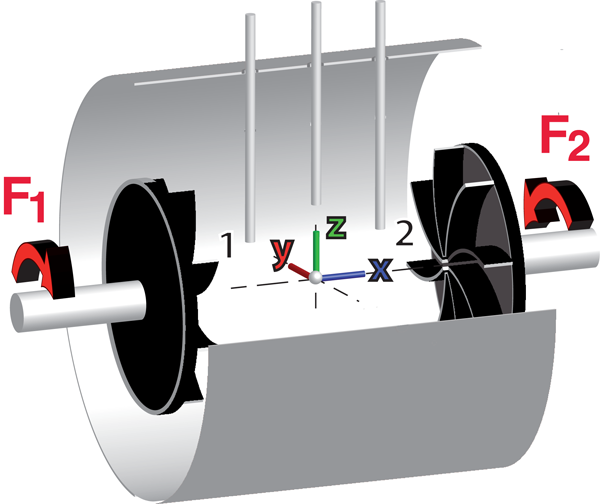
The experiments by Gallet et al. use a cylinder with two rotating disks located near the two ends of the cylinder (see Fig. 1). The cylinder is filled with liquid sodium, and blades are mounted on the disks to improve the entrainment of the fluid by the disks. The disks rotate at independent rotation rates. In the simplest configuration, they counterrotate at equal angular velocities and set up a strong shear layer in the midplane of the cylinder. In addition to the azimuthal component of the velocity field, there is also a meridional flow, which drives fluid away from the rotating disks along the axis of the cylinder and back to the disks near to the walls of the cylinder. This so-called von Kármán flow is capable of sustaining a magnetic field, but the precise mechanism at work in the experiment is still a matter of discussion because the experiment never produced a magnetic field without some amount of ferromagnetic material incorporated into the rotating disks.
Two arrays of magnetic sensors mounted on rods next to each rotating disk allowed Gallet et al. to monitor the magnetic field in the two halves of the cylinder. When the two disks rotated at different rates, the magnetic field was stronger next to one disk than next to the other. This by itself is no surprise. If the velocity field is not symmetric, the magnetic field it generates does not have to be symmetric either. But the degree to which the magnetic field became localized in one of the two half cylinders is unexpected. An indication of a genuine localized magnetic field (of the type one envisions for the Sun during the Maunder minimum) is the fact that the asymmetry in the magnetic field was largest when the two disks rotated at rates different by about (when the magnetic energy measured by one array is ten times the energy measured by the other array), not when one of the two disks was at rest. It is a moderate, but not the largest possible, asymmetry in the velocity field that caused the largest asymmetry and strongest localization in the magnetic field. Similarly, the convective flow of the Sun cannot have been dramatically different during the Maunder minimum than at other times, and yet the Sun’s magnetic field was seemingly concentrating in one hemisphere.
Gallet et al. also propose a mechanism to explain their results. They reduce the full equations to a simple equation for the amplitudes of the dipole and the quadrupole components of the magnetic field. They show that if the critical magnetic Reynolds number required to generate a pure dipole or a pure quadrupole field are nearly equal, their nonlinear dynamics can create superpositions which localize the field near either one of the disks.
Some discussion is likely to follow Gallet et al.’s work on whether the observations in their experiment relate to localized fields in planets or stars whose dynamos operate in rotating bodies at higher magnetic Reynolds numbers and under various other conditions different from those realized in the experiment. But this work highlights the possibility that dynamo experiments could permit investigation of magnetohydrodynamic phenomena inaccessible numerically and could augment our understanding of the dynamo mechanism in planets and stars.
References
- B. Gallet, S. Aumaître, J. Boisson, F. Daviaud, B. Dubrulle, N. Bonnefoy, M. Bourgoin, P. Odier, J-F. Pinton, N. Plihon, G. Verhille, S. Fauve, and F. Pétrélis, Phys. Rev. Lett. 108, 144501 (2012)
- A. Gailitis et al., Phys. Rev. Lett. 84, 4365 (2000)
- R. Stieglitz and U. Müller, Phys. Fluids 13, 561 (2001)
- D. P. Lathrop and C. B. Forest, Phys. Today, No. 7, 64, 40 (2011)
- A. Tilgner, Phys. Earth Planet. Inter. 117, 171 (2000)