New Optical Route to Magnetic State Control
Devices that harness the spin of the electron (rather than solely its charge) to process and store information are the basis of spintronics. Currently, static forces are used to switch the magnetization in a spintronics device, but the vision for future devices is to be able to switch them at high speeds with short-pulsed laser light [1].
So far, pulsed lasers have mainly been a tool for heating a sample to a temperature where it is in a different magnetic phase. Laser heating a sample can modify the magnetization on a time scale of picoseconds (ps) [2]; however, in the absence of an external magnetic field, the heated regions will form multiple domains with an equal mixture of and magnetization. A better solution is to find a way to optically switch individual domains into a definite magnetic state.
Now, Johan de Jong, at Radboud University in the Netherlands, and colleagues report in Physical Review Letters that they have been able to accomplish this sort of magnetic state control in the insulator [3]. With short pulses of circularly polarized laser light, they flip the magnetization of a single magnetic domain within . de Jong et al. achieve this by taking advantage of the interaction between light of a certain helicity and a spin reorientation transition unique to the material they studied. The present finding is an important step for the complete light control of magnetic domains in a variety of magnets, and highlights an important light-matter interaction in magnets.
is a member of the class of materials called orthoferrites. Orthoferrites have a distorted perovskite structure, and exhibit a rich variety of thermally induced magnetic transitions [4]. In the case of , there are two magnetic phase transitions that are relevant to de Jong et al.’s work. The first occurs at a temperature , when the ions have a weak ferromagnetic moment along the axis. The second occurs at a temperature , when this ferromagnetic moment rotates to the axis. (The iron magnetic moments are actually antiferromagnetically ordered, but a small symmetry breaking interaction causes them to cant in the same direction, which is why they have a weak ferromagnetic moment.)
de Jong et al. have confirmed that a linearly polarized pulse of light can heat an orthoferrite that is below to above the phase transition in of order a picosecond, a time scale that is mainly determined by the characteristic time for spins to exchange heat with the surrounding lattice. In this nonequilibrium state, the spin structure changes in the same manner as the thermally induced spin reorientation transition: the magnetization flips from being aligned along the axis to being aligned along the axis. However, if there is no magnetic field, the magnetization vector is equally likely to be oriented or along the axis, so multiple domains form.
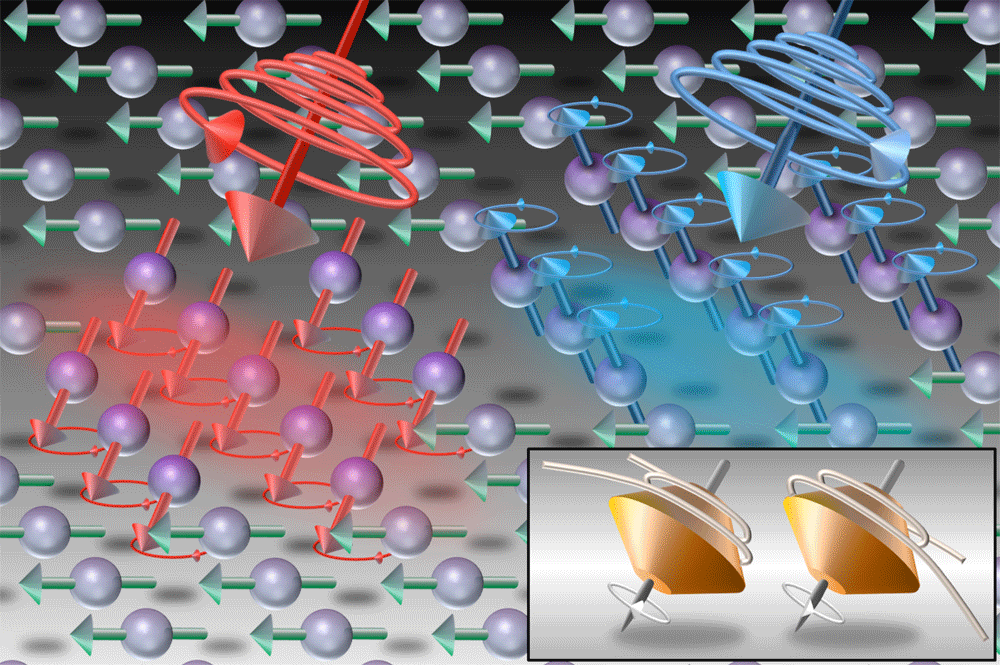
To have a better control over the final state of the domains, de Jong et al. use circularly polarized light to perform the switching. The electric field vector associated with circularly polarized light rotates clockwise or counterclockwise around the light’s direction of propagation. Circularly polarized photons therefore carry angular momentum, which makes it possible for these photons to flip a spin. de Jong et al.’s idea is that the helicity of light can selectively drive a spin excitation in a solid via a coherent optical process, an effect that the group reported several years ago [5]. In orthoferrites, the spin precession is known to occur at gigahertz to terahertz frequencies [6], a speed that is accessible for commercially available pulsed lasers.
The group uses a state-of-the-art optical pump and probe method to control domains in a roughly -micrometer-thick plate of . First, a circularly polarized pulse acts as a “pump,” in that it excites spin excitations. A second, linearly polarized pulse, acts as a “probe,” measuring the induced magnetization within a certain time delay after the first pulse. The second pulse is sensitive to the magnetization of the because of the Faraday effect: when light is transmitted through a magnetic material, its polarization rotates; the magnitude and sign of the rotation angle depend on the strength and orientation of the material’s magnetization.
The team takes a series of spatially resolved images of the Faraday rotation with a CCD camera, so they can identify the evolution of the magnetic domains. With this sophisticated method, de Jong and colleagues can study magnetic switching in time and space, and capture new insights into the nature of the spin dynamics in orthoferrites. Below , right-handed circularly polarized light can induce the magnetization, while left-handed circularly polarized light can induce the magnetization (Fig. 1). All parts of the sample in an illuminated region are converted to a single magnetic domain ( micrometers) within ps. These states stay in a particular magnetic orientation for up to nanoseconds without an external magnetic field. This experiment is thus a clear demonstration that the helicity of light can control the magnetization vector of the magnetic domain in insulating magnets.
An important result of de Jong et al.’s work is that they have identified the mechanism for exciting spins with light via impulsive stimulated Raman scattering [7] or the inverse Faraday effect [5], which yields the coherent spin excitation or magnon (the quanta of spin precession). To phenomenologically understand this, consider the light-matter interaction when a pulsed laser shines on a magnet. A spin wave can be coherently excited if the frequency difference, , of two photons with frequencies and is equal to the frequency of the spin-wave mode . The pulsed lasers de Jong et al. use have a wide bandwidth ( nanometers), so they contain many pairs of photons, which automatically satisfy the above resonant condition ( ). Furthermore, the lasers can produce an optical field with a pulse width that is shorter than the characteristic time of the spin wave, which acts as an impulsive driving force of the individual spins and thus the spins begin to precess. This allows them to determine the initial phase of the spin precession by the helicity of light with which they excite it.
Does the circularly polarized light alone induce the single magnetic domain? de Jong et al. show that the phase diagram of , in terms of sample temperature and pump fluence, is unique. In most magnets, magnetic domains with and magnetization have the same energy, but this is not the case in orthoferrites. This is because the spin orientation transition is second order, producing two local minimums in the potential with and magnetization. This means there are two possible routes to the phase transition and the final route depends on how the sample temperature reaches . Therefore the initial temperature, or, equivalently, the laser fluence, is also a crucial factor in determining the orientation of a single magnetic domain.
The control of spin excitations with light, which has also been demonstrated in antiferromagnetic with intense terahertz magnetic fields [8], is ideal for achieving ultrafast magnetic switching. It also opens a new way to produce emergent phenomena in a variety of materials. For example, orthoferrite is now known to be a ferroelectric, in which a spontaneous polarization appears in response to a magnetic field—though the temperature where this occurs is only [9]. Furthermore, the static magnetization of orthoferrite can be controlled by a static external electric field. Such a versatile magnetoelectric effect arises from the competition between multiferroic (ferroelectric plus magnetic) domains, which are mutually clamped by the mobile domain walls of ferroelectric and magnetic orders. In this multiferroic phase, spin excitations aren’t described by magnons. Instead, electric-dipole-active magnons, now referred to as electromagnons, appear [10]. Electromagnons may prove to be a useful medium for controlling multiferroic domains, and such electromagnons could be excited by the ultrafast optical techniques developed by de Jong et al. More broadly, this type of ultrafast magnetic switching is a versatile tool for controlling a wide variety of magnets.
References
- Discussion Meeting Issue, The spin on electronics, edited by S. Parkin, G. Aeppli, and B. Hickey, Phil. Trans. R. Soc. A 369, 3553 (2011)
- E. Beaurepaire, J. C. Merle, A. Daunois, and J. Y. Bigot, Phys. Rev. Lett. 76, 4250 (1996)
- J. A. de Jong, I. Razdolski, A. M. Kalashnikova, R. V. Pisarev, A. M. Balbashov, A. Kirilyuk, T. Rasing, and A. V. Kimel, Phys. Rev. Lett. 108, 157601 (2012)
- R. L. White, J. Appl. Phys. 40, 1061 (1969)
- A. V. Kimel, A. Kirilyuk, P. A. Usachev, R. V. Pisarev, A. M. Balbashov, and Th. Rasing, Nature 435, 655 (2005)
- A. M. Balbashov, G. V. Kozlov, A. A. Mukhin, and A. S. Prokhorov, in High Frequency Processes in Magnetic Materials, edited by G. Srinivasan and A. N. Slavin (World Scientific, Singapore, 1995), pp. 56-98[Amazon][WorldCat]
- Y-X. Yan, E. B. Gamble, Jr., and K. A. Nelson, J. Chem. Phys. 83, 5391 (1985)
- T. Kampfrath et al., Nature Photon. 5, 31 (2011)
- Y. Tokunaga, N. Furukawa, H. Sakai, Y. Taguchi, T. Arima, and Y. Tokura, Nature Mater. 8, 558 (2009)
- M. Kenzelmann, Physics 4, 88 (2011)