Rethinking the Neutrino
To some, this may be the year of the dragon, but in neutrino physics, this is the year of . Only one year ago, this supposedly “tiny” mixing angle, which describes how neutrinos oscillate from one mass state to another, was undetected, but the last twelve months have seen a flurry of results from experiments in Asia and Europe, culminating in the result from the Daya Bay Collaboration, now being reported in Physical Review Letters, that shows that is not small after all [1]. A not-so-tiny mixing angle forces us to rethink theory, calling for new explanations for why quarks and leptons are so different. It also opens the door to new experiments, potentially allowing the discovery of violation—a difference between neutrinos and antineutrinos that may be related to the matter asymmetry of the early universe.
Neutrino oscillations are a simple idea that can be derived in any intermediate level quantum mechanics class. In the weak interaction, neutrinos are produced and detected in “flavor” eigenstates—electron ( ), muon ( ), and tau ( ). However, the Hamiltonian depends on energy, which in turn depends on mass. In a simple two-neutrino model, with just the muon and electron flavors, the mass eigenstates ( and ) can be rotated with respect to the flavor eigenstates,
Mixing between flavor and mass states sounds strange, but quarks do it. Why shouldn’t neutrinos do it too?
A result of this mixing is that the neutrino born via the weak interaction in one flavor state will evolve with time to have some probability of interacting as the other flavor. The probability of this oscillation is equal to , in the (admittedly strange, but useful) units of (in meters, m), (in mega-electron-volts, MeV), and (in ). This formula depends on two fundamental parameters: the mixing angle, , which sets the amplitude for the oscillation probability, and the squared mass splitting, , which affects the wavelength of the oscillation. It also depends on two experimental parameters: , the distance the neutrinos have traveled from source to detector, and , the energy of the neutrino. While Eq. (1) is a simplified two-neutrino picture, expanding to the three known flavors, , , and , it follows a similar line of thought; in this case the two-dimensional rotation matrix with one angle, , becomes a three-dimensional matrix with three Euler angles: , , and .
The story of neutrino oscillations measurements begins with an article by Davis on a search for solar neutrinos that appeared in Physical Review Letters in 1964 [2] (also a year of the dragon!). But despite Davis’ subsequent discovery of a very obvious signature, it took a long time for physicists to understand and correctly interpret the data as a problem with the underlying particle physics. In the standard model, neutrinos are massless. This assumption is necessary to explain parity violation, a asymmetry in the spin dependence of beta decay. But if neutrinos have zero mass, in Eq. (1), the oscillation probability goes to zero, so oscillations cannot occur. The standard model was so successful in all other aspects of particle physics that it took years and many careful follow-up experiments for physicists to accept the experimental reality: neutrinos have mass and do oscillate.
As we have continued to study oscillations, we have learned that neutrinos are not like the other particles in many ways. For one thing, the mass splittings are very small compared to those of their charged particle partners. For another, two of the mixing “Euler” angles, and are very large—exactly the opposite of the mixing matrix seen in quarks. But the last mixing angle, , remained elusive, despite a dedicated search by two experiments: Palo Verde, in Arizona [3], and Chooz, in France [4]. Many people assumed that the was very tiny, partially inspired by the phenomenology of so-called tri-bi-maximal mixing [5]. In its purest form, this idea, put forward in to explain the pattern of mixing angles, requires . Various other theories gave order of magnitude predictions from to . Experimentalists responded by designing for small values. The present-generation experiments were designed to reach , but the Neutrino-Factory-of-Our-Dreams could potentially reach .
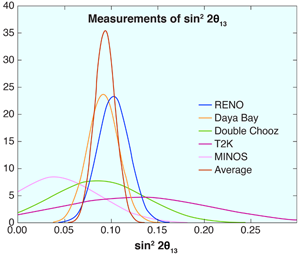
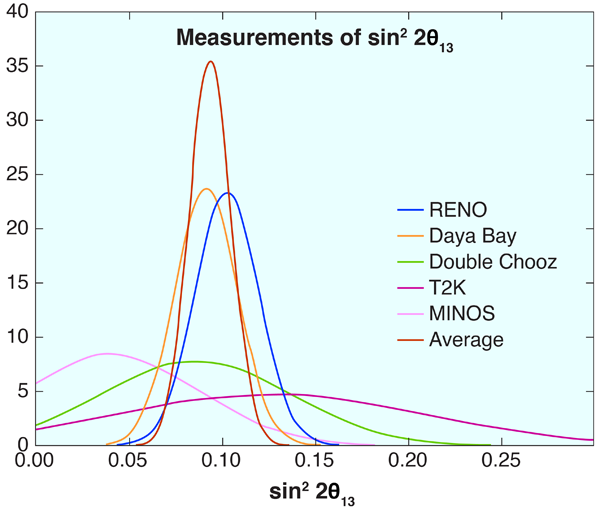
Suddenly, this view has changed. The first challenges to expectation have come from accelerator-based “appearance” experiments, which look for interactions of a new flavor ( ) in a sea of interactions of the original flavor ( ). While this sounds like a search for a needle in a haystack, in a well-designed experiment, like T2K in Japan (see 18 July 2011 Viewpoint) [6] and MINOS [7] at Fermilab in Illinois, the needle sticks out. Nevertheless, these experiments had low statistics and confusing results. The errors were relatively large and the results were still consistent with . But the central values were not tiny (see Fig. 1)—a first clue that was going to be larger than expected. Appearance experiments are problematic because, in the case of three neutrinos, they are sensitive to unknown parameters beyond , including the ordering of the mass states (called “the mass hierarchy”) and the -violating parameter. On the other hand, disappearance experiments have a much simpler oscillation formula, which reduces to .
Daya Bay, which is located in China, is illustrative of the new generation of disappearance experiments. This experiment is housed at one of the new ultrapowerful reactor complexes that are coming online worldwide. Reactors are copious sources of antielectron neutrinos ( ), for free! The idea is to search for antineutrino disappearance as a function of distance, so experiments have multiple detectors. Daya Bay uses six (Fig. 2). These can be placed at varying distances ( ) from the reactor source to trace the oscillation wave. The antineutrinos interact with free protons in the scintillator oil of the detector via an “inverse beta-decay” process that produces a positron and a neutron: . This interaction has a cross section known to high precision; the energy of the antineutrino can be fully reconstructed, and the positron followed by a subsequent neutron capture produces a coincidence signal that separates the signal from background. The development of long-lifetime gadolinium-doped scintillator was a crucial breakthrough in detecting , since this improves the neutron capture time by more than an order of magnitude.
In fact, the first reactor experiment to present a result was Double Chooz, in France [8]. The central value was again relatively large (Fig. 1), and at that point, it began to sink in: must be big. Within five months, Double Chooz’s experiment was followed by the Daya Bay result, [1]. In particle physics, a statistical significance of is needed to claim a discovery, and Daya Bay’s measurement was conclusive: is nonzero. The central value of their measurement was large and in excellent agreement with Double Chooz. Hot on Daya Bay’s heels was the result from the RENO experiment [9] in Korea, which yet again agreed with .
What does large mean? It means that the neutrino community is suddenly busy organizing workshops to re-think the next steps. With a well-measured value of we can pursue the mass hierarchy and the -violation parameter in appearance experiments that should come online soon. We shall see if measurements of these new parameters also defy expectations.
In one year, we went from knowing nothing, to having a full picture of this mixing angle. We found the dragon, and it roared!
References
- F. P. An et al., Phys. Rev. Lett. 108, 171803 (2012)
- R. Davis, Jr., Phys. Rev. Lett. 12, 303 (1964)
- F. Boehm et al., Phys. Rev. Lett. 84, 3764 (2000)
- M. Apollonio et al., Phys. Lett. B 466, 415 (1999)
- P. F. Harrison, D. H. Perkins, and W. G. Scott, Phys. Lett. B 530, 167 (2002)
- K. Abe et al. (T2K Collaboration), Phys. Rev. Lett. 107, 041801 (2011)
- P. Adamson et al. (MINOS Collaboration), Phys. Rev. Lett. 107, 181802 (2011)
- Y. Abe et al. (Double Chooz Collaboration), Phys. Rev. Lett. 108, 131801 (2012)
- S.-B. Kim et al. (RENO Collaboration), arXiv:1204.0626 (hep-ex); Phys. Rev. Lett. (to be published)