The super cool atom thermometer

A. M. Rey

Viewpoint

The super cool atom thermometer

JILA, NIST, and University of Colorado, Department of Physics, University of Colorado, Boulder, CO 80309, USA

December 7, 2009• Physics 2, 103

A new method of thermometry for ultracold atoms in optical lattices has the potential to accurately measure temperatures down to

50 pK

.

Figure caption — **Figure 1:** Spin gradient thermometry for ultracold atoms in optical lattices. In Ref. [8] a new thermometry method suitable for measuring temperatures of ultracold atoms in the Mott insulator regime was demonstrated. The method was applied to a two-component mixture of $^{87} Rb$ atoms in the Mott insulator regime. The two spin states used were the $F = | 1, - 1 〉 \equiv | ↑ 〉$ and $F = | 2, - 2 〉 \equiv | ↓ 〉$ hyperfine states. Since these two states have different magnetic moment, a magnetic field gradient induces a domain wall whose width is proportional to the temperature of the sample.

The conquest of the cold has become one the most exciting goals in modern atomic physics. The development of laser and evaporative cooling techniques have been among the greatest achievements in the second half of last century, as recognized by two Nobel prizes on these topics (1997 and 2001). These methods made it possible to reach temperatures of the order of a few $nK$ and led to the first experimental realization of a Bose-Einstein condensate [1,2] and a quantum degenerate Fermi gas [3] in dilute atomic vapors.

Even though $nK$ temperatures may seem extremely low, they are still too high for various potential applications, and the battle for reaching lower and lower temperatures in ultracold atoms continues. One of the driving forces for achieving even lower temperatures is Richard Feynman’s pioneering idea of a quantum simulator [4] wherein the behavior of a complex quantum system can be simulated by another quantum system. For instance, we want to load atoms in optical lattices (light shift potentials created by the interference of multiple laser beams) and use them to mimic the physics of electrons in solid-state crystals [5]. The optical lattice supplies the periodic potential in which atoms move. Bosonic (Fermionic) atoms in optical lattices are actually a perfect implementation of Bose (Fermi) Hubbard Hamiltonians [6], which describe particles hopping on a lattice with onsite interactions [7]. It is believed that these are the simplest models that contain the fundamental ingredients required to describe the behavior of strongly correlated materials, including, for example, quantum magnets or high-temperature superconductors. However, since atoms are much heavier than electrons, and since typical optical lattice interwell spacings are of the order of $10^{4}$ times the ionic lattice spacings, temperatures below $10^{- 2} nK$ are required in cold-atom laboratories in order to probe the same physics that occur at Kelvin temperatures in solid-state systems. The capability of reaching such low temperatures has to be accompanied by the development of new thermometers capable of measuring them. In a recent paper published in Physical Review Letters, David Weld and colleagues at the MIT-Harvard center for ultracold atoms [8] now report a new thermometry method for ultracold atoms in lattices, with the potential to measure temperatures as low as tens of $pK$ .

To date, typical bosonic cold-atom experiments in a single trap without an optical lattice have determined temperature from fits to absorption images of the expanded gas [9]. The data are fit to a bimodal density distribution. The area under the central peak, linked to the Bose-condensed fraction, and a Gaussian fit to the wings, which assumes noninteracting thermal atoms are combined to infer temperature. This technique has been very successful in a broad range of experimentally relevant temperatures, however, when atoms are loaded into optical lattices its regime of applicability reduces considerably.

When atoms are loaded into a lattice they acquire an effective mass, which exponentially increases with the depth of lattice potential. As a consequence, the diluteness condition, which requires a small ratio between the mean interaction energy per particle to its kinetic energy, becomes invalid as the lattice potential depth is ramped up and the system enters the strongly correlated regime. Beyond a critical lattice potential depth, the average kinetic energy required for an atom to hop from one site to the next, $J$ , becomes insufficient to overcome the interaction energy cost, $U$ , and atoms tend to get localized at individual lattice sites, forming the so-called Mott insulator [10].

In a homogeneous system, Mott insulating phases occur only at integer densities; noninteger density contours lie entirely in the superfluid phase because there is always an extra particle that can hop without energy cost. In the presence of an additional parabolic trapping potential, both phases can coexist and the system exhibits a shell structure in which Mott insulating domains with $n$ atoms per lattice site are separated by a superfluid region from other Mott domains with $n - 1$ atoms per site.

Simple, direct thermometry of systems in the Mott insulating state has remained a challenge since methods relying on the noninteracting approximation fail. One of the most common techniques to estimate the temperature of a lattice gas is to measure the initial temperature of the gas before the lattice is switched on, and then determine the final temperature assuming the lattice is turned on adiabatically: One equates the entropy of the final state to that of the initial state and then deduces the final temperature from the initial temperature. However, the errors of this method are uncontrolled, not only because of the adiabatic approximation assumption, but also because of the difficulty of an accurate determination of the temperature dependence of entropy for the many-body system of interest.

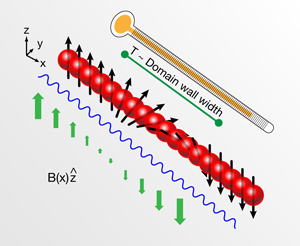
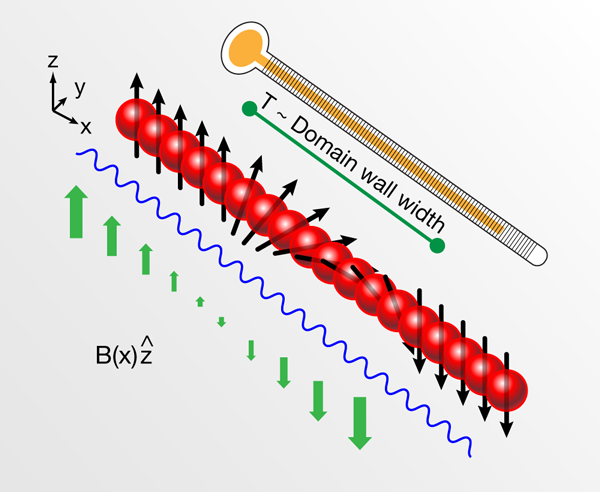
In their work, Weld et al. [8] have experimentally demonstrated a solution to this problem in a two-component Bose gas in the Mott insulator regime. In the experiment, the two spin states used were the $F = | 1, - 1 〉$ and $F = | 2, - 2 〉$ hyperfine states of $^{87} Rb$ atoms. Their strategy was to impose a magnetic field gradient and to use the mean magnetization of the gas as a thermometer (see Fig. 1). The basic idea can be understood by considering a spin- $1 / 2$ atom with magnetic moment $μ_{σ}$ , $σ = \pm 1 / 2$ . In the present of a magnetic field $B (x)$ , its mean magnetization is just $〈 σ 〉 = 1 / 2 tanh [- β Δ μ_{σ} \cdot B (x) / 2]$ with $Δ μ_{σ}$ the difference in magnetic moment between the two spin states, $β = 1 / (k_{B} T)$ the inverse temperature and $k_{B}$ the Boltzmann constant. For an incoherent mixture of atoms with spin independent interactions (condition well satisfied in $^{87} Rb$ atoms) the spatial and spin degrees of freedom can be factored out and the spin distribution becomes just $ρ (x) 〈 σ 〉$ with $ρ (x)$ the density distribution. By imaging the spin and density distributions, and knowing $Δ μ_{σ} \cdot B (x)$ , they were able to determine the temperature of the atoms by a standard fitting procedure.

The spin gradient thermometer was demonstrated to work in a range of temperatures not accessible to prior thermometry schemes. In the high-temperature regime, where interactions can be safety neglected, it agreed well with other methods relying on the noninteracting approximation, and was even shown to operate at temperatures high enough that no condensate existed before the lattice was ramped up. In the low-temperature regime it was used to measure a temperature as low as $1 nK$ , providing a direct demonstration that current experiments are able to operate deep in the quantum regime where the Mott insulator shell structure is well resolved. The lowest temperature measurable with the method is limited only by the experimental ability to resolve the domain wall ( $\sim 50 pK$ for current imaging resolution of a few $μ m$ ) and more fundamentally by $k_{B} T_{s} \sim J^{2} / U$ , the onset of super-exchange interactions (spin-spin interactions mediated by virtual tunneling process [11]), whichever is higher. Below $T_{s}$ the incoherent mixture approximation becomes invalid.

The development of experimental methods, such as the one reported in Ref. [8], capable of measuring subnanokelvin temperatures brings us one step forward towards the dream of using cold atoms to simulate and manipulate different strongly correlated many-body systems, which appear in various fields in physics, ranging from condensed matter to subatomic physics.

References

M. H. Anderson et al., Science 269, 198 (1995)
K. B. Davis et al., Phys. Rev. Lett. 75, 3969 (1995)
B. De Marco and D. S. Jin, Science 285, 1703 (1999)
R. P. Feynman, Int. J. Theor. Phys. 21, 467 (1982)
I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008)
D. Jaksch, C. Bruder, J. I. Cirac, C. W. Gardiner, and P. Zoller, Phys. Rev. Lett. 81, 3108 (1998)
J Hubbard, Proc. R. Soc. London A 276, 238 (1963)
D. M. Weld, P. Medley, H. Miyake, D. Hucul, D. E. Pritchard, and W. Ketterle, Phys. Rev. Lett. 103, 245301 (2009)
E. A. Cornell and C. E. Wieman, Rev. Mod. Phys. 74, 875 (2002)
M. P. A. Fisher, P. B. Weichmann, G. Grinstein, and D. S. Fisher, Phys. Rev. B 40, 546 (1989)
P. Anderson, Phys. Rev. 79, 350 (1950)

About the Author

Ana Maria Rey received her Ph.D. from the University of Maryland in 2004. Her Ph.D. research on ultracold bosonic atoms loaded in optical lattices was done in a combined program between the university and NIST, Gaithersburg. For this work, she received the 2005 DAMOP Thesis Prize. She followed her Ph.D. studies with a postdoctoral fellowship at the Institute for Theoretical Atomic, Molecular, and Optical Physics at the Harvard-Smithsonian Center for Astrophysics. In the fall of 2008 she became an associate fellow of JILA and a research assistant professor at the department of Physics at the University of Colorado. Her current research efforts focus on using ultracold atoms and molecules to study the physics of strongly correlated materials, to investigate nonequilibrium phenomena, to perform quantum information processing and precision measurements.