Protecting quantum superpositions from the outside world

Alexander Lvovsky

Viewpoint

Protecting quantum superpositions from the outside world

Institute for Quantum Information Sciences, University of Calgary, Alberta T2N 1N4, Canada

October 5, 2009• Physics 2, 83

An entangled state of six photons could potentially carry quantum information over large distances and between different reference frames.

Figure caption — **Figure 1:** Parametric down conversion generates pairs of photons in an entangled, orthogonal-polarization state. In their experiment, Rådmark *et al.* focus on events where three indistinguishable pairs are produced when a UV pulse passes through a non-linear crystal. The photons in each pair are emitted in different directions, so the “six-pack” can be separated into two sets of three (green beads). The photons are then separated from each other using beam splitters (purple rectangles) and sent into polarization analyzers – beam splitters (blue rectangles) that transmit or reflect the photon depending on its polarization - and finally, single-photon detectors. The black rectangles marked “U” depict unitary polarization transformations used to analyze the generated state and verify its robustness against collective noise.

Quantum information science relies on superpositions of quantum states with a definite phase relation, but such superpositions are inherently fragile against interactions with their environment. Fortunately, if some kind of common property bounds these interactions, it is possible, though by no means easy in a practical setting, to come up with states that are essentially immune to their environment. In papers appearing in Physical Review A and Physical Review Letters, Magnus Rådmark and Mohamed Bourennane at Stockholm University in Sweden and Marcin Wiśniak and Marek Żukowski at Uniwesytet Gdański in Poland report that they have prepared a six-photon entangled state that is immune to the environmental disturbances commonly occurring in optical fibers [1].

In contrast to classical bits that can only be in a logical state of either $0$ or $1$ , the quantum bit can be prepared in a linear combination of states, which in formal notation we would write as $| 0 〉 + | 1 〉 / \sqrt{2}$ . A good example of a quantum bit is a single photon traveling down an optical fiber. A photon in a horizontal polarization state, which we can denote by $| H 〉$ , can encode logical $0$ , while a vertically polarized photon, $| V 〉$ , represents a logical $1$ . A superposition state of $(| H 〉 + | V 〉) / \sqrt{2}$ would then be represented by a photon oriented at 45° to horizontal, while $(| H 〉 + i | V 〉) / \sqrt{2}$ is the same as a circularly polarized photon, with other combinations existing as well.

With multiple quantum bits, we can form more complex superpositions, such as $(| H 〉 | V 〉 - | V 〉 | H 〉) / \sqrt{2}$ , which we will call $| Ψ^{-} 〉$ . In this case, we have two photons with orthogonal polarizations, but we don’t know which photon is horizontal and which is vertical. Such a state is said to be entangled because of its indivisible nature: its properties cannot be described by treating each photon separately.

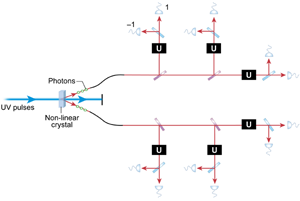
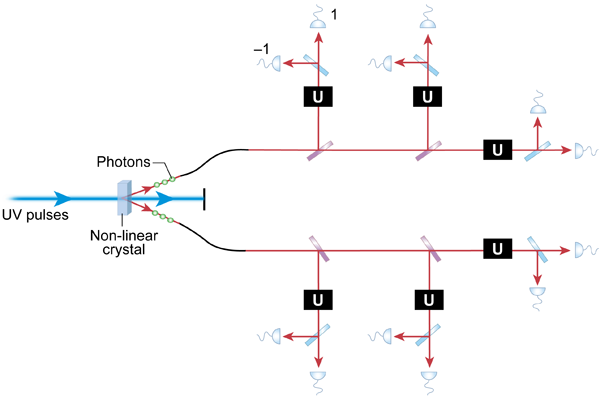
Entangled photon states can be prepared using a process called spontaneous parametric down conversion. This is a nonlinear optical phenomenon where a photon, forming a part of a strong pump laser beam propagating through a crystal, spontaneously splits into two photons of lower energy (Fig. 1). The geometry of the crystal and the fields can be arranged in such a way to produce entangled states of photons with different polarizations.

Entangled photon states permit massive parallelism because when we perform a physical operation on one or both photons, we simultaneously affect all terms in the superposition. This is the source of the power of quantum information processing. Unfortunately, quantum superposition states in general, and entangled states in particular, are extremely fragile. For example, we could use a polarization-maintaining optical fiber to make sure that horizontally and vertically polarized photons entering a communication channel are undeterred as they propagate. This would keep the classical content of the information carried by the photons intact. However, a superposition state would likely be destroyed in the same fiber because the horizontal and vertical components will travel at different phase velocities, and the phase relationship, or coherence, between the components that defines the quantum information content, will be lost. Even worse, the fiber, potentially being a part of an underground cable, will be subjected to mechanical stresses and temperature fluctuations that change the phase shift every few milliseconds, making it virtually impossible to even keep track of it.

The most straightforward way to tackle this problem is to try to isolate quantum processors or communication lines from the environment as much as possible. An alternative method, proposed in the late 1990s [2], relies on the fact that in many cases there is only one specific class of interactions with the environment that is the most significant in leading to a loss of coherence. We can then encode information into states that are immune against this particular decoherence mechanism—called decoherence-free states—to prepare robust quantum bits.

As an example, suppose we couple two photons into a fiber (that is not necessarily “polarization-maintaining”) and separate these photons by a time interval as short as a few nanoseconds—much less than the time scale of the environmental fluctuations. Then, even though the transformation is completely random, it will be almost exactly the same for both photons. Can we use this property (the decoherence of this type is called collective noise) to construct decoherence-free states?

The answer turns out to be yes. In fact, a simple calculation can show that the state $| Ψ^{-} 〉$ has the property of being immune to collective noise. If we launch two photons in this state into a fiber, then no matter how much their polarization is twisted and turned during the propagation, the photons emerging from the other end will still be in the state $| Ψ^{-} 〉$ , as long as both photons are affected identically. However, this state by itself is insufficient for quantum computation or communication, because one needs at least two states to encode a bit.

It turns out that as many as four photons are needed in order to construct a decoherence-free set of states that could fulfill this need. In 2004, Harald Weinfurter and colleagues in Germany employed parametric down conversion to prepare two four-photon entangled states that are invariant with respect to collective noise. They checked that when all four photons are subjected to the same polarization rotation, the states remain the same [3].

In their papers, Rådmark et al. have synthesized a six-qubit singlet—an entangled state of as many as six photons that is robust against identical rotations (a unitary transformation) of each individual component.

Why is this interesting? Six photons is the minimum needed to encode an arbitrary logical state of two quantum bits in order to protect against collective noise. In particular, by using six photons, one can encode, and send over an optical fiber, an entangled state, which will arrive intact no matter how significant the collective noise is [4]. In addition to protecting against fluctuations of the transmission channel, this state allows two observers who do not share a common reference frame (i.e., how they define “vertical” and “horizontal” polarizations) to communicate. In other words, if the sender is in Africa, and the receiver in Australia, their stations are not likely to be oriented the same way. The effect of the difference in orientations is similar to the collective noise and thus can be neglected if the decoherence-free encoding is used.

How do Rådmark et al. produce the six-qubit singlet? Following the traditional approach for making entangled states, they start with UV femtosecond laser pulses and use parametric down conversion to create entangled photons of a lower frequency. They constructed their experimental setup to maximize the rate of pair production to such a degree that the probability to produce not just one, but two, and even three pairs from a single laser pulse was non-negligible. This was a challenging technical task, given that parametric down conversion is a purely quantum, spontaneous phenomenon and normally has quite a low probability of occurrence.

The researchers focused on the three-pair events. They separated the photons into two sets of three according to the emission directions (left side of Fig. 1), then the photons within each triplet were separated from each other using beam splitters. Then they subjected each photon to a polarization measurement using a polarizing beam splitter (an optical element that transmits light in the horizontal polarization and reflects vertical) followed by avalanche photodetectors. By looking at the correlation statistics of photon detection events, Rådmark et al. verified that the state entering the polarization analyzers is close to the six-qubit singlet. The quantum overlap of the experimentally observed and theoretically expected state equalled $88 %$ , which is very high according to the current standards of multiphoton interference experiments.

The researchers checked the immunity of the state they prepared with respect to collective noise by transforming the polarization of each photon in the same way (using wave plates, represented in the figure by the black “U”s) and verifying that the correlation statistics did not change. They performed a number of further tests, just for fun; in particular, they checked and quantified the entanglement of the six-qubit singlet.

A careful reader may ask: How do the authors know that the desired state is generated before it is detected, and thus destroyed? The answer is, they do not. With each pump pulse, the down-converter process produces a random number of photon pairs. Furthermore, even if we could guarantee that exactly three pairs are produced, we cannot be sure that each triplet is split so that exactly one photon goes into each polarization analyzer. Thus Rådmark et al.’s six-qubit singlet cannot yet be used for practical applications. The situation would be different if the researchers had a tool to detect a photon without destroying it or learning about its polarization. Unfortunately, this tool is beyond the modern technology, albeit theoretically possible. Still, the ability to “postselect” a six-qubit state is of great significance for fundamental quantum-optical information research.

References

M. R Rådmark, M. Wieśniak, M. Żukowski, and M. Bourennane, Phys. Rev. A 80, 040302 (2009); M. Rådmark, M. Żukowski, and M. Bourennane, Phys. Rev. Lett. 103, 150501 (2009)
P. Zanardi and M. Rasetti, Phys. Rev. Lett. 79, 3306 (1997); D. A. Lidar, I. L. Chuang, and K. B. Whaley, 81, 2594 (1998)
M. Bourennane et al., Phys. Rev. Lett. 92, 087902 (2004)
A. Cabello, Phys. Rev. A 75, 020301 (2007)

About the Author

Alexander Lvovsky received his B.S. in physics at the Moscow Institute of Physics and Technology in 1993, and completed his Ph.D. in physics at Columbia University in 1998. He did post-doctoral research at the University of California, Berkeley, and at the Universität Konstanz in Germany (as an Alexander von Humboldt fellow), where he ultimately became a Group Leader in quantum-optical information technology. In 2004, he took the position of Associate Professor in the Department of Physics and Astronomy at the University of Calgary, where he remains today. Dr. Lvovsky is a Tier II Canada Research Chair, a lifetime member of the American Physical Society, and the winner of the Alberta Ingenuity New Faculty award and the Emmy Noether research award of the German Science Foundation. His research interests are in the synthesis, manipulation, measurement, and storage of quantum information carried by light for applications in quantum information technology.