How the tail wags the dog in ultracold atomic gases

Eric Braaten

Viewpoint

How the tail wags the dog in ultracold atomic gases

Department of Physics, Ohio State University, Columbus, OH 43210 USA
and Bethe Center for Theoretical Physics, University of Bonn, Bonn, Germany

February 2, 2009• Physics 2, 9

Recent calculations of the properties of ultracold atoms have revealed how two-body interactions at very short distances determine essential properties of many-body systems.

Figure caption — **Figure 1:** (a) In the BEC limit, all the atoms are in pairs with different spins (blue and red balls) that are bound together into diatomic molecules (grey circles) that form a Bose-Einstein condensate. In some of the diatomic molecules, the pairs are very close together (highlighted boxes). (b) The unitary limit is intermediate between the BEC and BCS conditions. (c) In the BCS limit, a tiny fraction of the atoms form very large Cooper pairs (grey circles). A small fraction of the atoms are very close together (highlighted boxes).

The development of the field of ultracold atoms has opened up new frontiers in both few-body and many-body physics. Of particular interest are universal aspects that apply equally well not only to various species of atoms, but also to other types of particles with short-range interactions. In the current issue of Physical Review A, Shizhong Zhang and Anthony Leggett of the University of Illinois report their derivations of some remarkable properties of ultracold atomic gases that exploit interesting connections between few-body and many-body physics [1].

A many-body system of atoms has many length scales. The length scales associated with the number density and the temperature are the typical separation of the atoms and their typical deBroglie wavelength, respectively. In addition to these many-body length scales, there are length scales associated with the interactions between the atoms, most of which are comparable to or smaller than the range of interatomic interactions. An important possible exception is the scattering length $a_{s}$ , which is the strength of $s$ -wave (isotropic) scattering, the dominant scattering mode at very low energies. The scattering length can be large compared to the range of the interatomic interactions. If it is large, the atoms have universal properties. There is a well-behaved but nontrivial limit in which the range is taken to zero while $a_{s}$ remains nonzero. This “zero-range” limit captures the universal aspects of systems of fermions with two spin states. The universal features apply to any fermionic atom for which the scattering length of the two spin states is much larger than the range of interatomic interactions. They also apply to the neutron, which has two spin states, despite the range of the interactions between neutrons being smaller by six orders of magnitude.

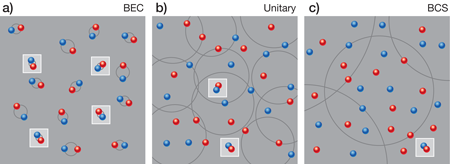
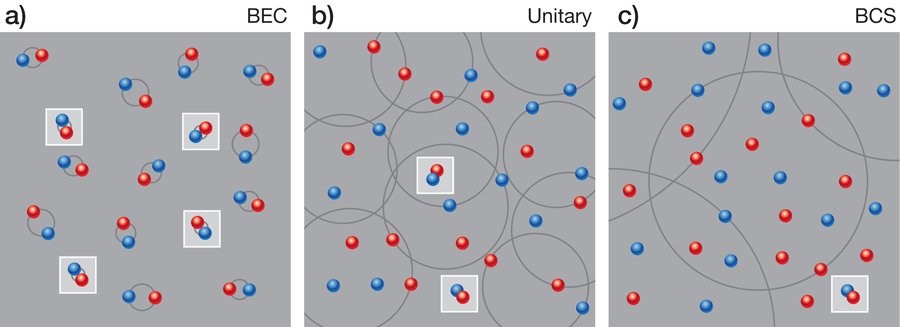
Zhang and Leggett call the universal many-body system the “two-component ultracold Fermi gas along the BEC-BCS crossover.” It is sometimes referred to more concisely as the strongly interacting Fermi gas. The ground state of this system is a superfluid, but the mechanism for superfluidity is completely different in the two weakly interacting limits. In the BEC (Bose-Einstein condensate) limit, the scattering length goes to zero through positive values $(a_{s} \to 0^{+})$ and we have a gas of bosonic diatomic molecules with weak repulsive interactions [Fig. 1(a)]. In the BCS (Bardeen-Cooper-Schrieffer) limit, the scattering length approaches zero through negative values $(a_{s} \to 0^{-})$ and we have a gas of fermionic atoms with weak attractive interactions [Fig. 1(c)]. In the BEC limit, the mechanism for superfluidity is the condensation of diatomic molecules, while in the BCS limit, it is the formation of Cooper pairs. Despite the dramatic difference between these two mechanisms, there is a smooth crossover between them as $a_{s}$ increases from $0^{+}$ to $+ \infty$ , jumps discontinuously to $- \infty$ , and then increases to $0^{-}$ . In particular, there is a well-behaved unitary limit as $a_{s} \to \pm \infty$ [Fig. 1(b)]. This limit is particularly interesting, because the system is so strongly interacting that the interactions provide no length scale.

The universal zero-range limit is relevant to experiments on ultracold atoms, because at the extremely low number densities and temperatures that can be achieved in cold trapped atoms, the many-body length scales are large compared to the range of interatomic interactions. A unique feature of ultracold atoms is the possibility of controlling the interaction strength experimentally. In particular, by tuning the magnetic field in the region near a Feshbach resonance, the scattering length can be varied over its entire range, from its off-resonant value through $\pm \infty$ and back to its off-resonant value. The use of Feshbach resonances to study the strongly interacting Fermi gas has been one of the major thrusts of experimental cold atom physics in the last decade.

Zhang and Leggett [1] derive some remarkable universal properties of the strongly interacting Fermi gas. They show that several of its important properties depend on the number density $n$ and temperature $T$ only through a dimensionless function $h (n, T, a_{s})$ that has a smooth unitary limit as $a_{s} \to \pm \infty$ . They derive the rate of change of the total energy per particle with respect to the inverse scattering length while $n$ and the entropy are held fixed:

where $k_{F} = (3 π^{2} n)^{1 / 3}$ is the Fermi wave number. This implies that E/N and other thermodynamic functions can be determined from $h$ by integration. Zhang and Leggett also showed that several other important properties of the system can be expressed as $h$ multiplied by a factor that is entirely determined by two-body physics, including (i) the interaction energy per particle, (ii) the rf spectroscopy shift, which is the shift in the radio-frequency signal required to change the spin state of an atom, and (iii) the rate for the photoassociation of pairs of atoms into a diatomic molecule using a laser beam. What these quantities have in common is that they are sensitive to the presence of pairs of atoms with different spins whose separations are much smaller than the many-body length scales and the scattering length. Thus the function $h$ is a measure of the density of pairs with small separations.

The existence of this function $h$ that plays such a central role in the strongly interacting Fermi gas was first realized by Shina Tan in 2005. Tan showed [2] that the momentum distribution in an arbitrary state of the system has a large-momentum tail of the form $C / k^{4}$ , where $k$ is the wave number and $C$ , which is called the contact, is the same for both spin states. He derived an expression for the total energy of the system that implies item (i) above as a simple consequence. Tan then derived a more general result [3] than Eq. (1) that applies not only to homogeneous states but also to any state of the system, including few-body states:

where the contact $C$ is the same quantity that appears in the asymptotic momentum distribution. The contact is the integral over the system of the contact density, which is proportional to the number of pairs of atoms with different spins that are close together. Tan’s results reveal that this number is much larger than one might expect. The number in a small volume scales like (volume) $^{4 / 3}$ instead of like (volume) $^{2}$ as one might expect. In a later paper, Tan derived a virial theorem (that is, a relationship between kinetic and potential energy) for atoms trapped in a harmonic potential [4] and it also involves the contact.

Tan’s first two papers were almost completely ignored for several years and were not published until 2008 [2,3]. One contributing factor to the delayed appreciation for Tan’s work was that he derived his universal results from the many-body Schrödinger equation by using novel methods involving generalized functions that he invented specifically for this problem. Zhang and Leggett, apparently unaware of Tan’s work, derived their results independently using more conventional methods of many-body physics. The first published paper that recognized the importance of Tan’s work was by Punk and Zwerger [5], who showed that the rf spectroscopy shift was proportional to $d E / d a_{s}^{- 1}$ . This result was derived independently by Baym, Pethick, Yu, and Zwierlein [6]. In 2008, Tan’s universal relations were rederived by Braaten and Platter using methods of quantum field theory [7] and by Werner, Tarruell, and Castin using less formal methods [8]. Werner, Tarruell, and Castin also derived independently the result on the photoassociation rate.

The universal relations discovered by Shina Tan and the applications that were subsequently derived [1,5,6,8] are beautiful illustrations of the interplay between few-body physics and many-body physics. They involve quantities that can be expressed in a factored form, with one factor involving many-body physics and the other involving only two-body physics. They exploit the analytic solution of the two-body problem in the zero-range limit. There may be important generalizations of these universal relations for which the few-body factors involve three or more particles. The three-body factors may be calculable using the exact numerical solutions of the three-body problem in the zero-range limit.

References

S. Zhang and A. J. Leggett, Phys. Rev. A 79, 023601 (2009)
S. Tan, Ann. Phys.323, 2952 (2008)
S. Tan, Ann. Phys. 323, 2971 (2008)
S. Tan, Ann. Phys. 323, 2987 (2008)
M. Punk and W. Zwerger, Phys. Rev. Lett. 99, 170404 (2007)
G. Baym, C. J. Pethick, Z. Yu, and M. W. Zwierlein, Phys. Rev. Lett. 99, 190407 (2007)
E. Braaten and L. Platter, Phys. Rev. Lett. 100, 205301 (2008)
F. Werner, L. Tarruell, and Y. Castin, arXiv:0807.0078

About the Author

Eric Braaten carried out his graduate work in theoretical high-energy physics at the University of Wisconsin, receiving his Ph.D. in 1981. After postdoctoral positions at University of Florida and Argonne National Laboratory, he took a faculty position at Northwestern University in 1995, where he conducted ground-breaking research on quantum chromodynamics. He moved to Ohio State University in 1995, where he has branched out into the field of ultracold atoms. Dr. Braaten was awarded the Humboldt Research Prize in 2009, and is now visiting the Bethe Center for Theoretical Physics at Bonn University. He continues to work on both low-energy and high-energy problems in elementary particle physics and on both few-body and many-body aspects of ultracold atoms. Dr. Braaten was chosen as a Fellow of the American Physical Society in 2000 and named an Outstanding Referee in 2008.