The complexities of simplicity

Paulo Bedaque

Viewpoint

The complexities of simplicity

Department of Physics, University of Maryland, College Park MD, USA

July 12, 2010• Physics 3, 58

Theoretical analysis of parallel layers of ultracold fermionic atoms reveals a rich variety of novel phases that might offer analogies to phenomena in other areas of physics.

Figure caption — **Figure 1:** Parallel layers of fermionic atoms offer rich new physics. One species of fermionic atoms (A) is constrained to move only on two thin layers separated by distance $d$ . Another species (B) is free to move in three-dimensional space. (a) At large interlayer separation, the A atoms only interact within a layer as they are dominated by $p$ -wave interaction, forming a BCS-type pairing as shown by the rotating atoms. (b) If the interlayer spacing is small, the A atoms will pair up across layers. (c) If the interaction between A and B species is strong, they will form “molecules” or (d) three-body Efimov states involving A atoms in each layer and a B atom.

Much of the interest in cold atom traps stems from their amazing tunability. Systems can be created with different species of bosons and/or fermions, different densities and dimensionality, some living in a continuum, and others on an artificial lattice [1]. Even the strength of the atomic interactions can be continuously adjusted at will through the use of Feshbach resonances [2]. Not surprisingly, many of these systems of trapped atoms are engineered to be analogs of other systems that are hard to crack theoretically or that cannot be accessed experimentally. Sometimes the relation between two models is quantitative, as is the case between neutron matter at subnuclear densities and a dilute gas of spin- $1 / 2$ fermions near a Feshbach resonance. Other times it is more of a loose analogy. In either case, these analogs can provide many useful insights, so the development of any kind of cold atom system with rich physics is welcomed.

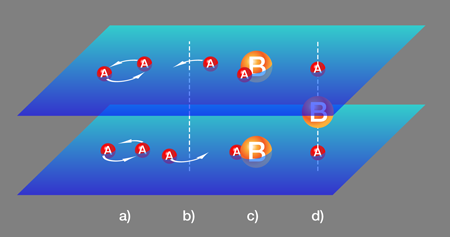
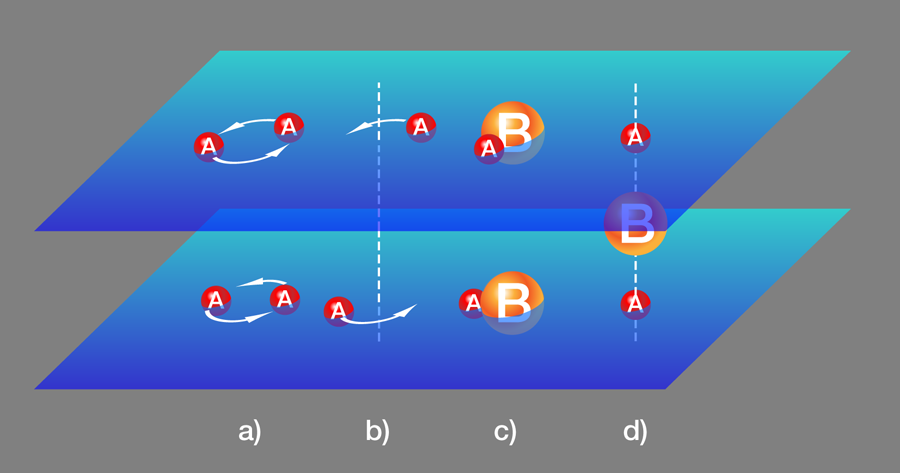
In fact, the imagination of theorists and the skill of experimentalists appear to be on the rise. A recent example is described in a paper in Physical Review A by Yusuke Nishida at the Massachusetts Institute of Technology, US [3]. The arrangement of atoms he considers is very simple (Fig. 1). Two spin-polarized fermionic atoms, A and B, interact through a tunable, $s$ -wave short-ranged potential. The A atoms are confined to live in one of two parallel layers separated by a distance $d$ , created by an optical lattice. Meanwhile, the B atoms are free to move in three-dimensional space. In the absence of B atoms, the A atoms are essentially free. They don’t interact across the layers because they are physically separated, and the interaction within the same layer is small since it’s dominated by the smaller $p$ -wave interaction. However, the A atoms do interact with the B atoms, and the B atoms can mediate the interactions between A atoms, even across layers if the distance $d$ is small enough. This setup is both experimentally feasible and very rich in terms of physical consequences.

The potential generated by the B atom mediation can be easily calculated, at least in perturbation theory, and is a steep function of the distance. The resulting interaction between A atoms will then depend on two tunable parameters, the A-B scattering length $a_{eff}$ and the distance between layers $d$ . The potential between two A atoms in the same layer depends on $a_{eff}^{2}$ ; the potential between A atoms in different layers depends on $a_{eff}^{2}$ and also on $d$ .

It turns out that if the parameter $1 / a_{eff}$ is large (in units of the Fermi momentum) and of either sign, or if $d$ is small or large, a very reasonable guess can be made for the qualitative properties of the ground state. To see that, let us take $1 / a_{eff}$ to be large and negative. This corresponds to A atoms with small attraction towards each other. When $d$ is large, the interaction between different layers is turned off and the ground state will be a weakly coupled $p$ -wave BCS superfluid [Fig. 1(a)]. But if $d$ is small, the interaction between the layers will dominate and A atoms in one layer will pair up with A atoms in the other layer in an $s$ -wave interaction [Fig. 1(b)].

Let us now look at the opposite limit, where $1 / a_{eff}$ is large and positive. The interaction between A and B atoms is strong and leads to the formation of tightly bound A-B atoms [Fig. 1(c)]. The interaction between these A-B molecules is small, so the A-B molecules Bose condense when cooled. The A atoms, however, live in a two-dimensional world and simple entropy arguments (and a rigorous result, the Mermin-Wagner theorem [4]) show that the continuous phase symmetry cannot be spontaneously broken as it would in three dimensions. Instead, we have a low-temperature phase with correlations decaying with a power law, while at high temperatures the correlations decay exponentially with distance due to the disordering effect of proliferating vortices. Separating these two phases is the Kosterlitz-Thouless phase transition [5]. This will happen whether or not the two layers are close to each other, as long as the distance $d$ is larger that the size of the molecules.

The difference between these three phases—BEC, power law correlations, and exponential correlations—is qualitative. Each corresponds to a different pattern of spontaneous symmetry breaking and their properties are not analytically connected to each other. This is unlike the more studied case of the BCS-BEC transition in the two-species spin- $1 / 2$ gas. There, one has either a weakly coupled superfluid BCS state or a weakly interacting gas of condensed dimers, depending on the sign of the scattering length. But the spontaneous symmetry-breaking pattern in both cases is identical and these two states are actually smoothly connected.

There is still one more phase related to the physics of the Efimov effect [6] that appears in the system for small interlayer distance. Consider two particles, either bosonic or distinguishable (they could be different spin states of the same particle) and let us assume their interaction can be described by a potential with range $R$ . For weak potentials they will not form a bound state; for large coupling there will be a deep bound state with spatial size similar to $R$ . In both cases the low-energy scattering of one particle into the other is described by a small scattering length $a$ , either positive or negative, comparable to the range $R$ . However, for a narrow range of potential strengths, a bound state (or a virtual bound state) will appear near zero binding and the low-energy scattering will be described by a scattering length much larger than the range $R$ . Since the wave function of this state is extended well beyond the reach of the potential it has a universal quality in the sense that it is largely independent of the precise shape of the potential.

Now, bring a third particle into the system whose interaction is also fine-tuned for two-body bound states that exist near the threshold. Back in the 1930s, Thomas [7] showed that the three-particle system would collapse, that is, the ground state would have a size of the order $R$ and an energy of order $- 1 / M R^{2}$ . In the1970s, Vitaly Efimov clarified the situation by arguing that the Schrödinger equation for the three-particle system, in the distance range between $R$ and $a$ , reduces to the Schrödinger equation of a particle in a $- 1 / r^{2}$ potential [6]. This potential is scale invariant and, by itself, does not have a ground state. Scale invariance is broken at short distances by $R$ , which stabilized the system giving the ground state as shown by Thomas, and at large distances by the scattering length $a$ . In between, one finds a logarithmic sequence of bound states where each binding energy is smaller than the next by a fixed numerical factor (about $515$ in the case of three identical bosons of equal mass). This sequence of shallower and shallower (and spatially larger and larger) bound states is cut off when their sizes reach $a$ . In the limit of $a$ going to infinity, an infinite sequence of bound states arises. This is the Efimov effect. In the bilayer system, three-body bound states appear for small interlayer distance and large $a_{eff}$ . They are composed of one B atom and two A atoms, one in each layer, and are analogous to the Efimov states, except that they live in two dimensions. In this region of parameter space we expect, then, a gas of fermionic trimers [Fig. 1(d)].

For large or small $d$ and large $| a_{eff} |$ , the phases discussed above are very likely to occur. What happens at intermediate values of $d$ and $| a_{eff} |$ is anybody’s guess and the analytic tools we have available break down. We can only “easily” understand phases that are weakly coupled, either because the interaction between the atoms is small, or because the forces are so strong that small-sized bound states are formed that interact weakly with each other. In each case, we have a weakly coupled theory in terms of appropriate degrees of freedom. Experimental and numerical work will be necessary to unravel the phase diagram where no such weakly coupled descriptions are evident.

Many generalizations of the setup proposed by Nishida naturally spring to mind. For instance, if atom B is a boson, the Efimov-like three-body bound state is also a boson and can condense, a mechanism competing with the condensation of B atoms themselves. What if two different species B and B’ live in bulk? The physics of these layered ultracold atomic systems is very rich indeed.

References

C. E. Wieman, D. E. Pritchard, and D. J. Wineland, Rev. Mod. Phys. 71, S253 (1999)
C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, Rev. Mod. Phys. 82, 1225 (2010)
Y. Nishida, Phys. Rev. A 82, 011605 (2010)
P. C. Hohenberg, Phys. Rev. 158, 383 (1967); N. D. Mermin and H. Wagner, Phys. Rev. Lett. 17, 1133 (1966); S. Coleman, Comm. Math. Phys. 31, 259 (1973)
J. M. Kosterlitz and D. J. Thouless, J. Phys. C 6, 1181 (1973)
F. Ferlaino and R. Grimm, Physics 3, 9 (2010)
L. H. Thomas, Phys. Rev. 47, 903 (1935)

About the Author

Paulo Bedaque received his Ph.D. in particle physics form the University of Rochester, and after postdoc stints at MIT and at the Institute for Nuclear Theory at the University of Washington, became a Divisional Fellow and Senior Scientist at Lawrence-Livermore National Laboratory. He is now an Associate Professor at the University of Maryland at College Park. His research addresses a variety of topics in nonperturbative QCD (lattice QCD, effective field theories), the physics of dense hadronic and quark matter, and topics in cold atomic traps.