Raising the temperature on density-functional theory

Emil Prodan

Viewpoint

Raising the temperature on density-functional theory

Physics Department, Yeshiva University, New York, NY 10016, USA

November 22, 2010• Physics 3, 99

A new analysis clears some of the remaining hurdles to a completely rigorous density-functional theory for calculating the properties of materials at finite temperature.

Figure caption — **Figure 1:** The Legendre transform is a valuable tool in classical mechanics and thermodynamics, and involves mapping a function of a coordinate to a function of a “derivative” of a coordinate. In some cases, the transform can be useful in converting a poorly behaved function into a well-behaved one. The Legendre transform of a functional $f [x]$ is defined as $f^{*} [q] = {sup}_{x} {〈 x, q 〉 - f [x]}$ . The diagram exemplifies the concept for a function of single variable. Given a slope $q$ , one determines the maximum value of $q x - f (x)$ shown by the double arrows. This maximum value occurs at the point marked by the arrow, and gives the Legendre transform $f^{*} (q)$ . If $f (x)$ is differentiable at the point where this maximum occurs, then $f^{*} (q)$ is given by the intersection point between the tangent to the graph and the vertical axis, and $q = d f / d x$ . Eschrig used the Legendre transform to derive new properties of the density-functional theory for finite temperature applications.

A recent NSF overview [1] highlights advances in “creating materials” on the computer, but goes on to state that “most useful compounds are still discovered by old-fashioned trial and error, guided by the researchers’ knowledge, experience, and educated guesses.” However, theoretical materials design is constantly improving, often based on abstract mathematical constructs, and this is made particularly evident in a paper in Physical Review B by Helmut Eschrig of the Leibnitz Institute for Solid State and Materials Research in Dresden, Germany [2].

The most widely used methods in quantitative materials design and characterization are density-functional theory (DFT) developed by Walter Kohn and his collaborators [3,4], and quantum chemistry methods developed by John Pople [5]. Kohn and Pople were awarded the Nobel Prize in Chemistry for the year 1988. There cannot be a more beautiful account of the history of DFT than the one given by Walter Kohn in his Nobel Prize lecture [6]. During a sabbatical in Paris in 1963, Kohn discovered that metallurgists had put a great deal of effort in mapping the electron density $n (r)$ in alloys and that they developed certain empirical reasoning based on these electron density maps. He wondered if electron density could completely determine the electronic properties of a material.

The electronic properties of the condensed matter phase are determined by the Coulomb interaction between electrons and by the external potential $v (r)$ generated by nuclei. While the Coulomb interaction remains the same in all materials, the external potential varies from one material to another, and so the question filters down to whether (ignoring electron spin) two external potentials can generate the same electron density. Pierre Hohenberg and Walter Kohn, sharing offices at the time, found a beautiful and astonishingly simple result: two potentials that differ by more than a constant cannot produce the same electron density. The electron density determines $v (r)$ , which in turn determines the Hamiltonian, which in turn determines all—equilibrium and nonequilibrium—properties of the system. As Kohn puts it [6], in principle, we should be able to compute the $17$ th excited state of an electron system from an accurate map of the electron density.

Hohenberg and Kohn also established a variational principle that says that there exists a universal functional $F_{H K} [n]$ (that is, a map defined on a set of functions that assigns a value to each function), acting solely on the electron density $n (r)$ , such that the ground-state energy of an electron system is given by (where $inf$ stands for infimum, or lowest value in a series):

The practical value of the above finding became even more apparent in a subsequent paper by Kohn and Sham [4], who showed that the Euler’s equations (that is, the expressions that express the variation for the above minimization problem) can be cast in the form of a set of nonlinearly coupled one-particle Schrödinger equations, now known as the Kohn-Sham equations.

There are three important things to note here. First, the formalism provides a method to compute the ground-state energy $E_{0}$ for a given position of the atoms’ nuclei. The configuration in which each atom occupies its equilibrium position is the one that minimizes $E_{0}$ . Furthermore, $E_{0}$ allows one to compute the forces acting on atoms, which opens the way for first-principles simulations of the vibrational spectra, chemical reactions, ab initio molecular dynamics, and so on [7]. Second, $F_{H K} [n]$ —coined the “divine” functional by Ann Mattson [8]—is universal; it works without modifications for all electron systems. Hence, simple model systems that can be tracked analytically lead to good functional approximations. Third, small incremental steps, exactly as advocated in the original Ref. [3], can lead to accurate functionals with broader and broader range of applicability.

In his paper, Eschrig touches on several aspects of DFT. He reminds us that a functional is not well defined until its domain—the densities that go into the variational principle of Eq. (1)—is established. His work also brings up the issue of nonuniqueness when the spin plays a role, which is shown to be irrelevant at finite temperatures. But most important is the claim by Eschrig that a finite-temperature functional can be defined that is differentiable for all densities (and magnetizations) that come from an equilibrium grand canonical state. This reassures us that the exact functional does not have some peculiar discontinuous behavior. (In the following, I cover these three issues in some detail, so some readers may wish to skip ahead to the last three paragraphs if not interested in the technical specifics.)

Originally, $F_{H K} [n]$ was defined on the set $A_{N}$ of density function $n$ ’s that are ground-state densities, that is, $n$ ’s that take the form (where $N$ is the number of electrons):

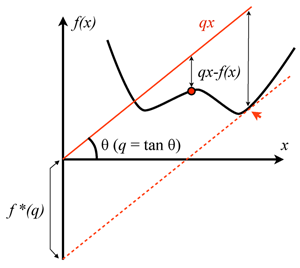
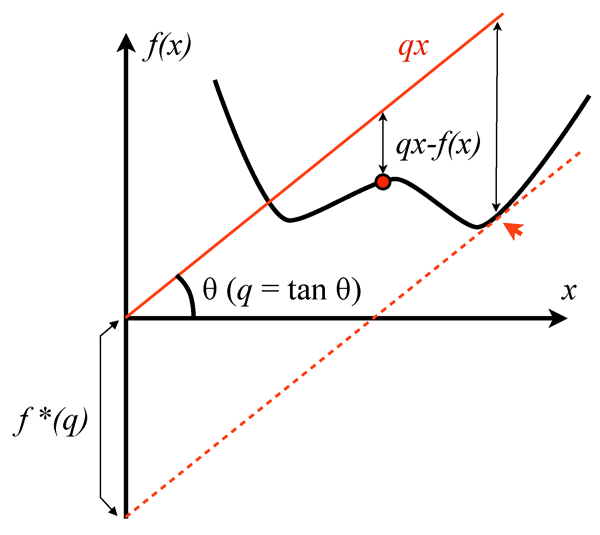
with $Ψ$ being the ground state of an electron system. This set $A_{N}$ can be a very wild set, whose properties are still very poorly understood. Lieb, in his remarkable take on the problem [9], discovered that $A_{N}$ is not even “convex” (that is, a linear combination of $n$ ’s that are in $A_{N}$ may fall outside of $A_{N}$ ). As Lieb very graphically puts it, the space $A_{N}$ has holes in it. This raises serious problems for any practical variational calculation, because it can get “stuck” in one of these holes, and, as a way out, Lieb proposed alternative (convex) functionals, defined on larger domains that can be explicitly characterized. His tool was the Legendre transform (see Fig. 1), which was also adopted in Eschrig’s work.

The philosophy behind the use of Legendre transformation is the following. One starts from the ground-state energy of a many-electron system, which is viewed as a functional $E [v]$ of the potential $v (r)$ . Deciding the domain of this functional is much easier because we have two guiding principles for potentials: the many-body Hamiltonian has to be self-adjoint and it has to be bounded from below. Note that both these properties can fail if the real-valued external potential is too singular, and this restricts the allowed potentials to a precise set. Once $E [v]$ is set, the density functional is defined via the Legendre transform of - $E [v]$ ( $sup$ stands for supremum, or the maximum value in a series):

The Legendre transform not only gives the expression of $F [n]$ but also provides a well-behaved domain for $F [n]$ , which can be explicitly characterized. Now, by taking a Legendre transform on $F$ (or a double Legendre transform on $E [v]$ ) we are brought back to $E [v]$ and therefore we can write:

which is nothing else but the Hohenberg-Kohn variational principle. Thus the Legendre transform allows one to reformulate the variational principle on a (convex) set of densities that can be explicitly characterized $[F [n]$ as defined in Eq. (3) has additional improved properties over the $F_{H K}$ defined in Eq. (1)].

Now, if one is to minimize the right-hand side of Eq. (4) using the corresponding Euler equation $δ F / δ n = 0$ (with the appropriate constraints), we first must make sure that the functional derivative $δ F / δ n$ (called a Fréchet derivative) exists at least at the points where the minimum is achieved (there is a simple example in Eschrig’s paper illustrating what happens when such derivative is ill defined). Eschrig notices that this might be problematic at zero temperature, as one can see by looking at $E [v]$ itself. In $R^{3}$ , if we squeeze $v (r)$ too much, the electrons start leaking at infinity, while on the torus, ground-state degeneracies can occur, both leading to a bad behavior for $E [v]$ . Eschrig’s key observation is that at finite temperatures and finite volumes, the grand canonical potential $Ω_{β} [v]$ , which takes the role of $E [v]$ , is free of such problems and its functional derivative is well defined for all allowed $v$ ’s. This allows him to conclude that $F_{β} [n]$ , also defined via a Legendre transform on $Ω_{β} [v]$ , has a Fréchet derivative at all densities that come from an equilibrium grand canonical state.

Eschrig builds on the seminal work of Mermin [10], which provided the variational principle for the grand canonical potential. As in the first paper on DFT, there is no discussion of Euler’s equation in Ref. [10]. The finite-temperature Kohn-Sham equations were presented in the 1965 paper of Kohn and Sham [3], but an explicit derivation was missing. The reader will find an explicit derivation and a very instructive discussion of these equations in Eschrig’s work.

Additionally, when the spin of the electrons is taken into account, the proper DFT procedure is to couple them to a scalar potential $v (r)$ and a magnetic vector field $B (r)$ . The goal is to establish a unique correspondence between the density $n (r)$ and magnetization density vector $m (r)$ on the one hand, and the $v (r)$ and $B (r)$ on the other. The degree of this uniqueness goes beyond the trivial additive constant seen in spinless DFT [11]. This may not pose serious problems [12], but it complicates matters. Fortunately, Argaman and Makov [13] noted that finite-temperature DFT is free of such complications. Eschrig’s work strengthens this view and, in addition, shows that the minimum of the functional can be found by solving its corresponding Euler equation, which can be cast in the form of the Kohn-Sham equations.

What does all this have to do with materials design and characterization? While DFT is, in principle, exact, in practice we have to rely on approximations. The available approximations have had a tremendous success in various applications, but there are still special classes of materials where their performance is rather poor. It is natural to ask if the current philosophy in functional development, relying on expansions around reference systems such as the uniform electron gas, will ever work for these special classes of materials. The search for the ”divine” functional, which presumably will allow scientists to sit at computers and design materials with predefined properties, could be greatly aided if we understand its general mathematical structure. But is the exact functional plagued with discontinuities that are too difficult to tackle? Eschrig’s work assures us that this is not the case, that in fact, the functional is smooth, at least for finite temperatures and volumes. The expansions of the density functionals around reference systems are not limited by singularities and are very likely to work. Eschrig’s analysis also points to another strategy for functional development based on an expansion around the high-temperature limit (a sort of $1 / T$ expansion). The analysis also provides a new test to assess the quality of an approximate functional. At last, given the smoothness of the functional, the transition from the variational principle to the Kohn-Sham equations can now be discussed in a much healthier mathematical framework.

References

Available at the official webpage http://www.nsf.gov/news/overviews/chemistry
H. Eschrig, Phys. Rev. B 82, 205120 (2010)
P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964)
W. Kohn and L. Sham, Phys. Rev. 140, A1133 (1965)
J. A. Pople, Rev. Mod. Phys. 71, 1267 (1999)
W. Kohn, Rev. Mod. Phys. 71, 1253 (1999)
R. Car and M. Parrrinello, Phys. Rev. Lett. 55, 2471 (1985)
A. E. Mattsson, Science 298, 759 (2002)
E. H. Lieb, Int. J. Quant. Chem 24, 243 (1983)
N. D. Mermin, Phys. Rev. 137, A1441 (1965)
H. Eschrig and W. E. Pickett, Solid State Commun. 118, 123 (2001)
W. Kohn, A. Savin, and C. Ullrich, Int. J. Quant. Chem. 101, 20 (2005)
N. Argaman and G. Makov, Phys. Rev. B 66, 052413 (2002)

About the Author

Emil Prodan received his Ph.D. from Rice University in 2003 for work on applications and foundation of density-functional theory. He spent two years at the University of California, Santa Barbara, as a postdoctoral scholar and two years at Princeton University as a fellow of the Princeton Center for Complex Materials. In 2007, he joined the physics department of Yeshiva University as an assistant professor. His current research combines pure mathematics, numerical analysis, and various models of condensed matter in a broad range of applications.