Invisibility cloak for ultrasonic waves

Che Ting Chan

Viewpoint

Invisibility cloak for ultrasonic waves

Che Ting Chan

Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China

January 10, 2011• Physics 4, 2

A cloak that can make an object undetectable by ultrasonic water waves has been successfully demonstrated.

Figure caption — **Figure 1:** The configuration of an acoustic cylindrical cloak for water waves. Cavities with large volume act as shunt capacitors, while narrow channels connecting them act as serial inductors.

Invisibility is perhaps one of the most intriguing of notions that have captured our imagination. In 2006, Schurig et al. [1] demonstrated that a shell of metamaterials could guide electromagnetic (EM) waves around a domain, thereby rendering an object inside that domain invisible. The idea is based on a mathematical technique called “transformation optics” [2–4], which establishes a correspondence between coordinate transformation and material parameters (the permeability and permittivity tensors). Such a technique allows us to design metamaterials that can, in principle, bend light any way we wish, including going around an object as if it is not there. In a paper appearing in Physical Review Letters [5], Shu Zhang, Chunguang Xia, and Nicholas Fang from the University of Illinois at Urbana-Champaign, US, report the successful design and realization of an acoustic cloak that can guide water waves around a domain so that any object placed inside is concealed. More importantly, they show that the cloak is effective for a fairly broad frequency range.

From a theoretical point of view, going from EM cloaking [1] to acoustic cloaking is fairly straightforward in two-dimensional (2D) geometry. By 2D here, we mean that the system parameters are uniform in one direction. In 2D, the Maxwell equations can be separated into transverse electric and transverse magnetic mode solutions and the wave equation for each polarization is identical in form to the acoustic wave equation. Cummer and Schurig [6] made specific use of this similarity and showed that the cloaking problem for acoustic waves can be solved with the same technique of transformation optics (it can be called “transformation acoustics”). The coordinate transformation that compresses a circle to a point [2,4], which generates the material parameters required for a cloaking shell for EM waves, will also generate a cloaking shell for acoustic waves in 2D. The material parameters are replaced by the mass density tensor components and the bulk modulus. So mathematically, the cloaking of 2D acoustic waves is straightforward, however, implementation is anything but. The problem is that the acoustic cloaking shell requires materials that have position-dependent properties with an anisotropic mass density profile.

Although such anisotropy and inhomogeneity are also required in EM wave cloaks, EM metamaterial research was already a fairly mature field by the time transformation optics was introduced. Several research groups had the capability to design resonators to realize different values of $ε$ and $μ$ , hence the realization of the EM wave cloak according to the transformation optics recipe was quickly demonstrated [1]. With acoustic waves it is a different story. While the notion of an acoustic metamaterial had already been introduced, and indeed realized in some systems for sound waves [7], the early designs did not address the issue of mass density anisotropy and the resonators typically required some soft material as a key component [7]. Since soft materials have strong absorption that would compromise invisibility, an alternative route is needed to realize the acoustic cloak in practice.

Zhang et al. [5] circumvented the difficulty using an innovative “transmission line” approach. It is well established in the microwave literature that a distributed network of inductors and capacitors can mimic a material with some specific values of $ε$ and $μ$ [8] in the sense that the currents and voltages traveling in a microwave circuit loaded with capacitors and inductors are counterparts of EM fields traveling in a material with corresponding values of $ε$ and $μ$ . By comparing the equations that govern the voltage and current in a distributed network with the Maxwell equations in a homogenous medium, we can map the voltage and currents to the fields, and the circuit parameters (capacitances and inductances) to material parameters ( $ε$ and $μ$ ). In this way, LC networks can be used to mimic a dielectric material and the analogy also works for negative refractive index materials. Due to such a mapping, LC networks have been used to demonstrate various phenomena associated with metamaterials, such as super-resolution focusing and negative refraction [8].

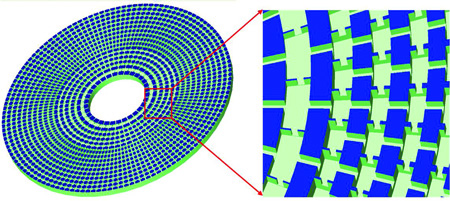
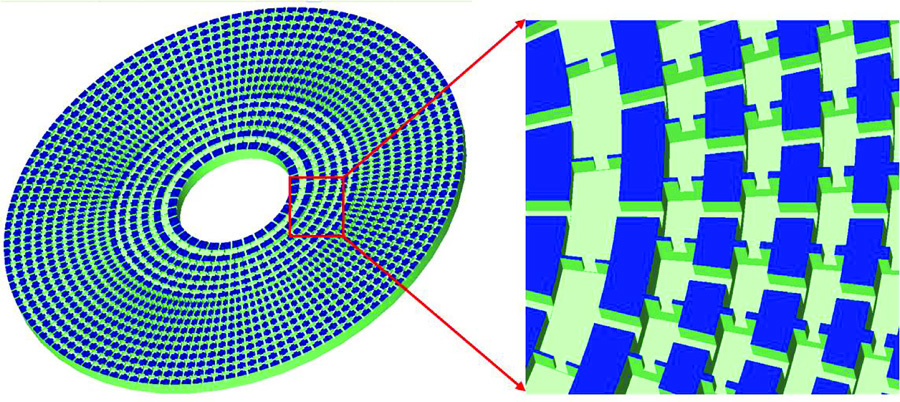
Zhang et al. [5] applied the idea to water waves in the ultrasonic regime. They designed an aluminum plate that has an array of cavities that act as acoustic capacitors (C), and the cavities are connected by channels that function as acoustic inductors (L) (see Fig. 1). The values of the acoustic L and C can be adjusted by varying the geometric parameters of the channels and the cavities. The concentric arrays of cavities and channels have spatially varying geometries so as to realize the different acoustic LC values needed for acoustic cloaking. We note also that the acoustic inductances and capacitances can be mapped to effective mass densities and compressibility, just as EM inductances and capacitances can be mapped to $ε$ and $μ$ . From another point of view, the ability of Zhang et al. to design the cavities with a specific profile of acoustic inductances and capacitances means that they can design a system in which the fluid behaves as if it has a specific spatial profile of effective mass density and compressibility, and if the profile matches that required for the cloaking shell, invisibility can be achieved.

The experimental implementation is further facilitated by some approximations to simplify the design. The authors employed the so-called “reduced” parameter set approach [1]. For different sets of LC parameters, the wave motion inside the cloak is the same, as long as they give the same product to preserve the effective refractive index point-by-point. The experimentalists thus have the freedom to choose different sets of acoustic L and C so as to avoid divergence of the radial component of the acoustic inductance at the inner boundary of the cloak [6]. This approach may compromise perfect impedance matching at the cloak boundary, but the experimental results show that the invisibility effect is still largely preserved using the “reduced” parameter set. Another approximation is the “discrete” implementation—a unit cell in the sample is of finite size although it is meant to mimic continuously varying functions in transformation optics. In Zhang et al.’s experiment, the unit cell is much smaller than the wavelength and so the effective medium approximation is very good. The end result is a cloak that guides water waves undisturbed around a circular domain as if the domain is absent. The cloaking effect is not perfect, due to the approximations used and some inevitable dissipation, but the effect is clearly illustrated.

We should further note that EM cloaking devices [1] usually have narrow bandwidth because the EM wave traveling inside the cloak has to detour around the cloaked domain and yet it has to catch up with the waves outside the cloak. This means that the phase velocity inside the cloak has to be faster than that of light traveling outside, which implies that the cloaking material has to be dispersive, which in turn implies severe bandwidth limitation. In acoustics, waves can, in principle, travel faster or slower inside the cloak than the outside medium, and the bandwidth limitation is inherently less severe.

The achievement of acoustic cloaking in this paper is perhaps not unexpected. In 2009, the same group demonstrated experimentally [9] that they could focus water waves through a network of identical Helmholtz resonators designed to mimic an acoustic metamaterial with negative mass density and negative compressibility. The authors went one step further in this paper: the effective mass density and compressibility are not constant but are “graded” in order for the acoustic metamaterial to bend waves. Their values change as a function of distance from the center, realized by varying the geometry of the cavities.

It would be interesting to see if one can cloak airborne sound waves. That would require engineered structures that induce an effective anisotropic mass density for air. A recent paper demonstrated such a possibility inside a corrugated cavity [10]. We also note that a cloak for surface waves has been designed by Farhat et al. [11].

References

D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, Science 314, 977 (2006)
J. B. Pendry, D. Schurig, and D. R. Smith, Science 312, 1780 (2006)
U. Leonhardt, Science 312, 1777 (2006)
A. Greenleaf, M. Lassas, and G. Uhlmann, Physiol. Meas. 24, 413 (2003)
S. Zhang, C. Xia, and N. Fang, Phys. Rev. Lett. 106, 024301 (2011)
S. A. Cummer and D. Schurig, New J. Phys. 9, 45 (2007)
Z. Liu, X. Zhang, Y. Mao, Y. Zhu, Z. Yang, C. T. Chan, and P. Sheng, Science 289, 1734 (2000)
G. V. Eleftheriades, A. K. Iyer, and P. C. Kremer, IEEE Trans. Microwave Theory Tech. 50, 2702 (2002)
S. Zhang, L. Yin, and N. Fang, Phys. Rev. Lett. 102, 194301 (2009)
D. Torrent and J. Sánchez-Dehesa, Phys. Rev. Lett. 105, 174301 (2010)
M. Farhat, S. Enoch, S. Guenneau, and A. B. Movchan, Phys. Rev. Lett. 101, 134501 (2008)

About the Author

Che Ting Chan is a Chair Professor of Physics and the Director of William Mong Institute of NanoScience & Technology at the Hong Kong University of Science and Technology (HKUST). He received his Ph.D. from the University of California, Berkeley, in 1985 and was a staff scientist at Ames Laboratory, Iowa, before joining HKUST in 1995. He is a fellow of the American Physical Society. His principal interests are the simulation of material properties, photonic/phononic crystals, metamaterials, and nanomaterials.