Harnessing nonlinearity for linear measurements

Hendrik Bluhm

Viewpoint

Harnessing nonlinearity for linear measurements

2nd Institute of Physics C, RWTH Aachen University, 52074 Aachen, Germany

April 4, 2011• Physics 4, 29

Researchers develop a new type of superconducting quantum interference device (SQUID) with significantly enhanced sensitivity and bandwidth, which can function as a general-purpose magnetic sensor.

Figure caption — **Figure 1:** (a) False color SEM micrograph of the dispersive SQUID magnetometer. The SQUID loop is shown in the inset. The fast flux line can be used to apply an external flux $Φ$ . (b) Schematic of the device. The flux bias circuit is shown on the left, and the crosses represent the Josephson junctions. An incoming microwave excitation signal (red arrow) is reflected (blue arrow) with a flux-dependent phase $ϕ$ . (c) The Josephson inductance of a Josephson junction is given by the slope of the sinusoidal $ϕ$ - $I$ relation and depends on the phase $ϕ$ across the junction. (d) Resonance curves for the oscillating current of the tank circuit and the phase $ϕ$ of the reflected microwave signal. A small change of the flux $Φ$ shifts the resonance frequency and is thus equivalent to a change of the excitation frequency. At large amplitude (blue), the nonlinearity of the inductance [see panel (c)] leads to a downshift of the resonance frequency as the resonance is approached, and thus a bending of the resonance curve towards the left. The resulting steeper dependence of $ϕ$ (red circle) on the applied flux leads to improved sensitivity.

The need to minimize the interactions of qubits with their environment makes their readout, which is an important component for quantum computing, a nontrivial endeavor. To meet this challenge, researchers have developed a variety of tools for ultrasensitive and high-bandwidth measurements and amplification. These include rf single-electron transistors for charge detection [1], Josephson bifurcation amplifiers for digital qubit readout [2], and parametric or SQUID-based [3] amplifiers for microwave signals with sensitivities at or even below the standard quantum limit [4].

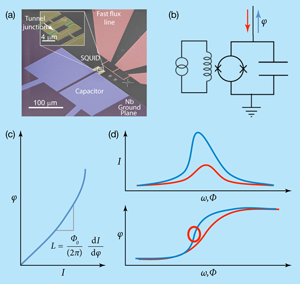
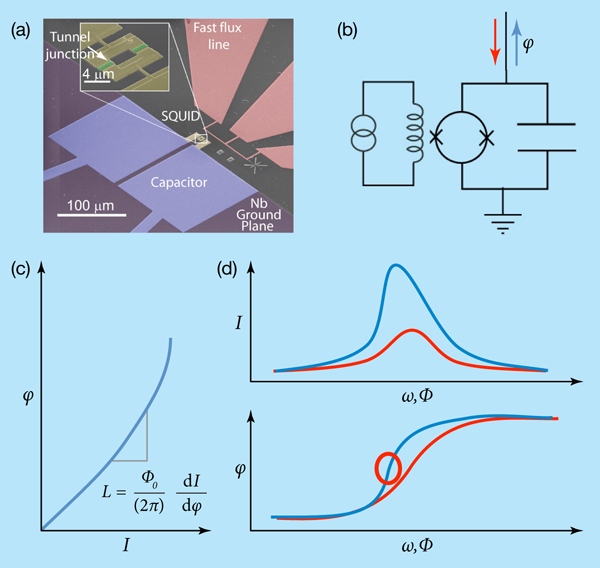
In a paper published in Physical Review B, Michael Hatridge and collaborators from Lawrence Berkeley National Laboratory and the University of California, Berkeley, incorporate some of these techniques and concepts into a novel type of superconducting quantum interference device (SQUID) [5] that is intended for use as a general-purpose magnetic sensor for micro- and nanoscale samples. With further development, similar devices could provide a very powerful tool for a wide range of experiments and sensing applications much beyond the field of quantum information. Contrary to standard SQUIDs, in this new device the measurement signal is encoded in the phase of a reflected microwave signal. Furthermore, by employing the intrinsic nonlinearity of the device, the authors achieve an impressive enhancement of sensitivity, corresponding to less than one photon above the standard quantum limit. Besides high sensitivity, this approach has the advantage of providing a large bandwidth and a low measurement backaction on the sample, compared to conventional SQUIDs.

A SQUID consists of a superconducting loop interrupted by one or two (sometimes even more) Josephson junctions. These junctions form weak superconducting links that can carry only a fairly small supercurrent $I$ , given by the Josephson relation $I = I_{c} sin (ϕ)$ , where $ϕ$ is the phase difference of the superconducting condensates on either side of the junction. The maximal achievable (critical) current $I_{c}$ depends on the nature of the junction. If such junctions are placed in a closed superconducting loop, gauge invariance and single-valuedness for the superconducting wave functions require that the sum of their phases equals $2 π Φ / Φ_{0}$ , where $Φ$ is the total magnetic flux through the loop and $Φ_{0} = h / 2 e = 20.7 G μ m^{2}$ is the superconducting flux quantum. As a result, a flux threading the loop induces a circulating current, which is analogous to the screening current in a superconducting loop without junctions, but usually much smaller.

The standard operating mode of such a SQUID [Fig. 1(a)] is based on measuring the largest supercurrent that can be carried between two leads, which are attached to the loop such that each arm contains one of the Josephson junctions [see Fig. 1(b)]. If the bias current exceeds this total critical current, a voltage drops across the no-longer superconducting device. The critical current is reduced if an applied flux induces an additional circulating current; thus measuring the $I$ - $V$ characteristic of a SQUID provides information about the flux threading its loop. There are two common ways to perform this measurement. The device just described is usually hysteretic, i.e., the bias current has to be returned to near zero for it to return to the superconducting state once a voltage develops. In this case, repeated current ramps can be used for signal averaging. Alternatively, it is possible to eliminate the hysteresis by shunting each of the junctions with a damping resistor. One obtains an $I$ - $V$ characteristic that shows no voltage up to the critical current, beyond which a steep rise of the voltage occurs. The position of this rise again depends on the applied flux. Since the $I$ - $V$ curve is now single-valued, changes in flux can be detected with a $dc$ measurement at fixed current or voltage bias.

Each of these procedures has certain disadvantages, namely, a large power dissipation while the device is in the voltage state, as well as dissipation and Johnson noise arising from the resistors, respectively. Hatridge et al. use a completely different approach by exciting the SQUID with a few $- GHz$ microwave signal without applying any dc voltage. As a result, no power is dissipated in the SQUID and no shunt resistors are necessary. In this mode of operation, the SQUID acts as a variable flux-dependent inductance $L$ . The fact that each of the junctions has a Josephson inductance $L_{J} = Φ_{0} / (2 π d I / d ϕ)$ for small signals can be seen from the Josephson relation and the fact that the voltage $V$ across the junction is given by $V (t) = (Φ_{0} / 2 π) d ϕ / d t$ . The important property of this Josephson inductance is its dependence on the junction current, which in turn depends on the flux through the SQUID loop. Since at typical operating frequencies $ω / (2 π)$ , the SQUID impedance ( $i ω L$ ) is much smaller than the $50 Ω$ impedance of standard microwave components, it is convenient to connect the device in parallel with a capacitor. The resulting $L C$ resonator acts as an impedance-matching tank circuit whose resonance frequency $ω_{R} = 1 / \sqrt{L} C$ depends on the measured flux via $L \approx L_{J} / 2$ . It is measured by connecting the device to the end of a single coaxial cable. Since the device contains no dissipative elements, a signal launched towards it is reflected without any amplitude loss. However, the phase of the reflected signal changes by $π$ as the frequency (or equivalently the flux) is swept through the resonance. The overall sensitivity depends on the drive power, the noise level of the amplifier used to amplify the reflected signal, and the derivative of the reflection phase with respect to the applied flux, which is largest at $ω = ω_{R}$ .

The analysis discussed so far assumes that the excitation signal is small enough for the SQUID to behave as a linear inductor. One of the main results of Hatridge et al. is a substantial increase of the sensitivity at larger drive amplitude, where nonlinearities become important. Due to the nonlinearity of the Josephson relation, the effective inductance of a junction (averaged over a signal cycle) increases for larger amplitudes of the oscillating current. The rise of the latter upon approaching the resonance frequency from below leads to an increase of the inductance and thus a drop of the resonance frequency. Hence the resonance is reached faster than in the linear small signal regime, and the resonance curve is bent towards lower frequencies, as shown in the top panel of Fig 1(d). The same phenomenon occurs if the resonance frequency is shifted toward a fixed operating frequency due to a change in the applied flux. This distortion of the resonance curve leads to a faster change of the reflected phase as a function of the applied flux and thus an improved flux sensitivity [Fig. 1(d), bottom]. Since the resonance curve eventually takes the shape of a breaking wave with a diverging maximum slope, very large gains can be achieved.

In order to gain insight into its noise performance, Hatridge et al. describe the operation of their device in terms of a parametric amplifier. Such an amplifier for ac signals is formed whenever the confining potential of a harmonic oscillator is modulated periodically. The modulation can amplify a small excitation that allows the parametric drive to supply energy to the oscillator and thus to increase its amplitude. In the present case, the parametric drive arises from the nonlinear response to the microwave excitation. The signal to be amplified can either be a flux signal, or an additional microwave signal sent into the excitation line. In the latter case, the device can act as a general purpose signal amplifier with a remarkably low noise temperature of about $0.2 K$ . For comparison, semiconductor-based cryogenic amplifiers typically have noise temperatures of a few kelvin [6]. This mode of operation was used by the same group to observe quantum jumps by continuously reading out the state of superconducting qubit [7].

Besides its high sensitivity and bandwidth, the advantage the SQUID parametric amplifier has over conventional SQUIDs is that by varying its excitation amplitude and flux bias point, one can tailor its characteristics to a given application. For example, it is possible to trade sensitivity against bandwidth and backaction, or to tune the operating frequency. The best flux sensitivity demonstrated by Hatridge et al. is $0.14 μ Φ_{0} / \sqrt{Hz}$ at a bandwidth of $0.6 MHz$ . With a noise level of $0.29 μ Φ_{0} / \sqrt{Hz}$ , the bandwidth can be increased to $20 MHz$ . Both operating points compare favorably with the parameters of conventional SQUID sensors, which can achieve noise levels as low as $0.02 μ Φ_{0} / \sqrt{Hz}$ [8], but more typically show values at least an order of magnitude larger. A direct comparison is difficult because of the tradeoffs between sensitivity, bandwidth, and backaction.

From the size of the device, one can estimate that its spin sensitivity would be on the order of a few hundred electron spins per $\sqrt{Hz}$ . The performance metrics could be improved further by optimizing the device geometry and parameters. It appears conceivable that such modifications would allow the magnetic detection of a single electron spin or magnetic molecule with reasonable averaging times. Other possible applications that would particularly benefit from the high bandwidth and/or low backaction include the measurement of persistent currents in metal rings [9], susceptibility measurements [10], characterization of nanomagnets, and vortex dynamics studies.

References

R. Schoelkopf, P. Wahlgren, A. Kozhevnikov, P. Delsing, and D. Prober, Science 280, 1238 (1998)
I. Siddiqi, R. Vijay, M. Metcalfe, E. Boaknin, L. Frunzio, R. J. Schoelkopf, and M. H. Devoret, Phys. Rev. B 73, 054510 (2006)
M. Mück, C. Welzel, and J. Clarke, Appl. Phys. Lett. 82, 3266 (2003)
M. A. Castellanos-Beltran, K. D. Irwin, G. C. Hilton, L. R. Vale, and K. W. Lehnert, Nature Phys. 4, 928 (2008)
M. Hatridge, R. Vijay, D. H. Slichter, J. Clarke, and I. Siddiqi, Phys. Rev. B 83, 134501 (2011)
The noise temperature is a measure of the sensitivity of an amplifier and specifies the temperature at which a resistor would produce the same amount of noise as the amplifier adds to its input signal
R. Vijay, D. H. Slichter, and I. Siddiqi, Phys. Rev. Lett. 106, 110502 (2011)
D. J. V. Harlingen, R. H. Koch, and J. Clarke, Appl. Phys. Lett. 41, 197 (1982)
Y. Imry, Physics 2, 24 (2009)
H. Bluhm, J. A. Bert, N. C. Koshnick, M. E. Huber, and K. A. Moler, Phys. Rev. Lett. 103, 026805 (2009)

About the Author

Hendrik Bluhm received his Ph.D. in 2008 from Stanford University and held a postdoc position at Harvard University until February 2011. He is now a professor of Physics at RWTH Aachen University. His main research interests are experiments on spin qubits and scanning techniques (in particular scanning SQUID microscopy) applied to topics from superconductivity, mesoscopic physics, and quantum coherence.