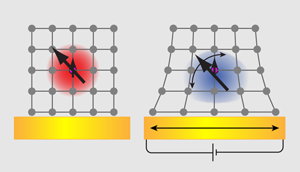
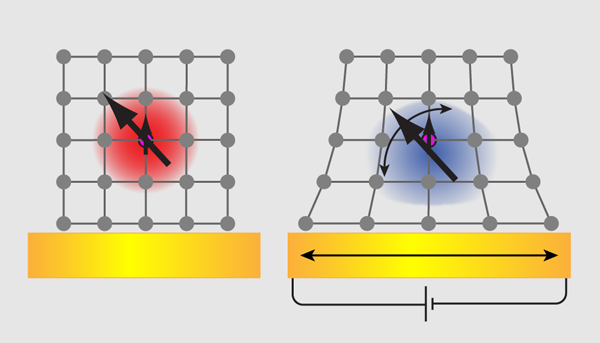
Spin qubits feel the strain

Brendon W. Lovett

Viewpoint

Spin qubits feel the strain

School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, United Kingdom

January 18, 2011• Physics 4, 6

Strain can be used to shift the resonant frequency of electron spin to the point where quantum processing starts looking feasible.

Figure caption — **Figure 1:** Schematic diagram showing the effect of strain on a crystal donor. (Left) With no voltage applied to the actuator (yellow), the crystal is unstrained; the electron donor wave function is depicted in red. (Right) A potential on the actuator strains the crystal, and alters the shape and energy of the wave function (blue). It brings the electron spin (long arrow) into resonance with an appropriately tuned microwave field.

The next frontier in information processing is the quantum computer. Such a device, which relies on the precise control of quantum states, promises revolutionary fast algorithms and the prospect of unbreakable codes [1]. Because most of our existing information technology relies on electrical and magnetic phenomena, the quantum magnetic moment, or spin of an object is a natural component of a quantum computer. A register of interacting spins is a very tempting prospect since it could allow not only binary state manipulation but also powerful quantum parallel algorithms. However, the delicate nature of quantum states makes its construction an extremely difficult task, and an astounding range of physical systems continue to be investigated as possible candidate devices. Writing in Physical Review Letters [2], Lukas Dreher and co-workers at the Walter Schottky and Walter Meissner Institutes in Garching, Germany, have taken an important step forward in the construction of a device based on silicon. They report that applying a local strain opens the way for control of spins on individual phosphorous donors.

To explain why this step is an important one, we must consider what is needed for the construction of a quantum computer. Like its classical counterpart, a quantum machine must have a range of features, such as memory, a processor, and networking facilities. However, there is no single quantum system that outperforms all others for each of the necessary functions [3]. To overcome this quandary, it is becoming fashionable to use more than one degree of freedom in candidate devices. For example, photons make good carriers of quantum information over large distances, whereas stationary registers of trapped ions can be used to store and process information. This kind of hybrid [4] architecture is particularly powerful in solid-state systems where many types of quantum particle exist together. It led Bruce Kane to produce his seminal work [5] in the late nineties, which described a silicon-based quantum computer. In his blueprint, the nuclei of a regular array of phosphorus donors are used to store the quantum information. They each possess a spin of one half—a quantum two-level system or qubit that is analogous to the classical bit in conventional digital logic. The nuclear spin is a good choice since it interacts very weakly with its environment, so spin relaxation happens more slowly and quantum states can be faithfully stored for many seconds.

One problem with the realization of Kane’s scheme is that nuclei do not naturally interact with each other very strongly, and this is where the spin of the extra electron provided by the donor (phosphorus has atomic number $15$ , one more than silicon) plays a key role. Adjacent donor electrons can overlap and their spin is associated with a much larger magnetic moment than the nucleus, resulting in a strong mutual coupling. The donor nuclei and electron also interact, as long as the spatial distribution of the electron (its wave function) has some amplitude at the nucleus. These two interactions allow an indirect coupling of the two adjacent nuclear spin gates, which allows execution of the required logic gate.

Kane’s design also allows nuclear spins to be addressed individually, thereby picking out exactly which qubits are involved in which gate operations. Using a nearby electrode and adjusting the potential on it, one can alter the amplitude of the electron wave function at the nucleus. The negatively charged electron will be more attracted to a positive potential on the electrode, and therefore be pulled away from the nucleus, reducing the coupling. This shifts the frequency at which the nuclear spin precesses in a magnetic field, and gives it a unique radio frequency (rf) resonance. By applying controlled pulses of rf radiation, the angle of each spin can be precisely controlled, as long as the bandwidth of each pulse only overlaps with the desired nuclear resonances. Consequentially, the rf bandwidth must be less than the electron-induced shift, and this is the fundamental limitation on the speed at which quantum operations can be performed.

Since Kane’s proposal, some improved schemes have been suggested to improve the speed and fidelity of quantum gates [6]. For example, the electron spin itself can be used directly as the qubit during logic operations. When the information needs storing for a long time, a combination of microwave and rf pulses can be used to move each electron state into the corresponding nuclear spin [7]. Individual addressability of the qubits remains crucial, and the same electrical control of the electron-nuclear coupling allows the same shift of the electron spin resonance frequency as it does of the nuclei. Bradbury and co-workers [8] experimentally demonstrated this kind of tuning, though in their experiments, antimony rather than phosphorus donors were used. They observed a maximum shift of $25 kHz$ , which is smaller than the width of the antimony electron spin resonance line; it could not therefore be directly used for addressing an individual donor, so investigating alternative approaches is important.

Now, Dreher et al. [2] have demonstrated one such alternative that can be used to generate much larger shifts. They show that the resonance frequency of an individual nuclear magnetic moment (spin) of a donor in silicon can be shifted by applying a local strain to the crystal, through use of a piezoelectric actuator (see Fig. 1). The resulting shifts are an order of magnitude larger than any observed before, and this means that the time it takes to perform a gate operation can be slashed by the same factor. The model $P:Si$ system is familiar, but the setup used has two extra important features. First, the whole sample is mounted on an actuator that can be compressed or stretched by applying a voltage to it (see Fig. 1). Second, a silicon-germanium ( $SiGe$ ) alloy is placed directly beneath the active donor layer. This alloy has a different spacing of atoms to the active layer, and so the active layer stretches as it tries to match the lattice of the alloy.

The positions of the nuclei and electrons surrounding the donor determine the potential energy landscape in which its electron sits—and so the size and shape of its wave function. Straining the crystal lattice should therefore result in a change of the electron wave function at the donor nucleus, and so alter the coupling between the two particles. The Garching-based team have shown that applying a potential to the actuator does indeed change the strain field at the donors and thus modifies the coupling dynamically. The effect is more pronounced in systems that are prestrained, hence the inclusion of the $SiGe$ alloy in the setup.

The team have managed to measure a strain-induced shift of $490 kHz$ , about twenty times larger than that seen in the antimony experiment and, crucially, twice the natural linewidth of the donor electrons. This means that individual donors could be singled out from all of the others in a quantum computing device made using strain-inducing actuator gates. The constraints of pulse bandwidth discussed earlier would mean a minimum gate operation time of about one millisecond. Recent unpublished work [9] has reported that quantum information can last for as long as $0.6 s$ in the phosphorus electron, theoretically allowing hundreds of gate operations before the quantum computer would fail. This may not be quite enough to reach the threshold for quantum error correction [1], but this is a fast moving field and we can expect significant improvements in the next few months: The bismuth donor, for example, has larger electron-nuclear coupling than phosphorus and is a promising alternative candidate [10].

The final piece of Kane’s proposal describes how a single spin can be measured, and the technique that the Garching team used to detect the shifts in the energy levels of spins closely follows Kane’s measurement prescription. The number of electron spins in the active region of the sample is much too small for the more common method of detection, which depends on the impact the spins have on an incident microwave field. Rather, the team use electrically detected magnetic resonance (EDMR). The idea here is to pass a current through the sample and look for changes in it that result from the donor spins changing from one orientation to another. It only works in certain systems, and in this case is due to positive and negative charge carriers (holes and electrons) recombining for one spin orientation, thus reducing the current in this configuration. EDMR has been shown to be sensitive down to one hundred spins [11], some eight orders of magnitude fewer than the best direct microwave methods. It is thought that this limit can be reduced to a single spin, and indeed another electrical method has recently shown such a sensitivity [12].

Through their innovative use of strain, Dreher et al. have brought us closer to realizing Kane’s proposal for a quantum processor made from donors in silicon. Elaborating this technique, possibly with different donor atoms, means we can hope that a prototype quantum computer relying on donors in silicon may be with us very soon.

References

M. A. Nielsen, and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000)[Amazon][WorldCat]
L. Dreher, T. A. Hilker, A. Brandlmaier, S. T. B. Goennenwein, H. Huebl, M. Stutzmann, and M. S. Brandt, Phys. Rev. Lett. 106, 037601 (2011)
P. Kok and B. W. Lovett, Introduction to Optical Quantum Information Processing (Cambridge University Press, Cambridge, 2010)[Amazon][WorldCat]
J. J. L. Morton and B. W. Lovett, Annu. Rev. Condens. Matter Phys. (to be published)
B. E. Kane, Nature 393 133 (1998)
R. Vrijen, E. Yablonovitch, K. Wang, H. W. Jiang, A. Balandin, V. Roychowdhury, T. Mor, and D. DiVincenzo, Phys. Rev. A 62, 012306 (2000)
J. J. L. Morton et al., Nature 455, 1085 (2008)
F. R. Bradbury, A. M. Tyryshkin, G. Sabouret, J. Bokor, T. Schenkel, and S. A. Lyon, Phys. Rev. Lett. 97 176404 (2006)
A. M. Tyryshkin and S. A. Lyon, data presented at the Silicon Qubit Workshop at the University of California at Berkeley, 24-25 August 2009
R. E. George, W. Witzel, H. Riemann, N. V. Abrosimov, N. Notzel, M. L. W. Thewalt, and J. J. L. Morton, Phys. Rev. Lett. 105, 067601 (2010)
D. R. McCamey, H. Huebl, M. S. Brandt, W. D. Hutchison, J. C. McCallum, R. G. Clark, and A. R. Hamilton, Appl. Phys. Lett. 89, 182115 (2006)
A. Morello et al., Nature 467, 687 (2010)

About the Author

Brendon Lovett is a Royal Society University Research Fellow in theoretical physics at Heriot-Watt University, Edinburgh, where he leads the Theory of Quantum Nanomaterials group (tqn.eps.hw.ac.uk). He is also an Academic Visitor at the University of Oxford. He received his D.Phil. in physics in 2001 from the University of Oxford, for work on low dimensional magnetism. He then held Research Fellowships at the Department of Materials, University of Oxford, where he performed theoretical research into quantum coherence in solid-state systems. He has continued these interests since moving to Heriot-Watt in October 2010. His active research areas include the implementation of quantum information processing, models of open quantum systems in condensed matter and quantum biology.