Out of Touch, But Not Out of Sync
In 1665, not long after his invention of the pendulum clock, Christiaan Huygens (1629–1695) in The Hague reported on “an odd kind of sympathy,” referring to the tendency of two clocks mounted on the same wooden beam to synchronize their pendulum movements such that they beat in opposite phases [1]. At first he suspected that induced air currents caused this synchronization, but he then correctly attributed it to “imperceptible movements” of the supporting structure. Only ten years later, and some ten kilometers away in Delft, Antonie van Leeuwenhoek (1632–1723), after his construction of the microscope, wrote about “incredibly thin feet, or little legs, which were moved very nimbly” [2]. He had discovered what we now call cilia, tiny whiplike appendages that protrude from a cell body and beat periodically in a way that propels the microorganism. Closely related to cilia are flagella, which have a similar internal structure, but are longer compared to the size of the “body” than cilia. (While a cell can be covered in cilia, like hair, it usually has only one or two flagella.) Besides helping microorganisms and sperm cells swim, cilia and flagella are involved in clearing mucous from the airways, establishing left-right asymmetry in embryonic development, and many other functions. The two scientists from the Dutch golden age could hardly have expected how, centuries later, their discoveries would become connected.
Writing in Physical Review Letters, Benjamin Friedrich and Frank Jülicher from the Max Planck Institute for the Physics of Complex Systems, Germany, present a minimal physical model that explains how the two flagella on swimming alga can become synchronized [3], beating in opposite directions like the swinging pendulums in Huygens’ clocks. Experimentalists have observed this flagellar synchronization and believe it helps the microorganisms swim more efficiently, but they have not been able to explain how the flagella interacted with each other.
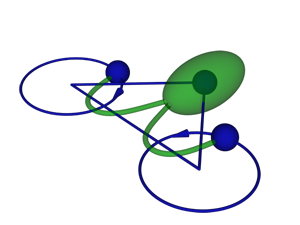
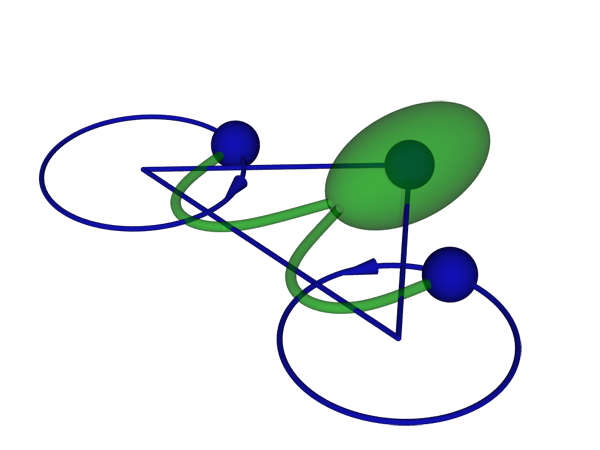
Friedrich and Jülicher study Chlamydomonas reinhardtii (Fig. 1), a unicellular green alga that swims thanks to two flagella that beat like the arms of a swimmer doing the breaststroke. However, this anthropomorphic description does not recognize the fact that the laws of fluid motion (hydrodynamics) are quite different in the microscopic world, where the Reynolds number (the ratio of inertial forces to viscosity) is low: for a swimming Chlamydomonas cell, it is around , and for a human swimming, around . The mirror-symmetric arrangement of two flagella is quite unique among microorganisms. When swimming in a straight direction, the two flagella move symmetrically [4], which allows a biflagellate swimmer to swim most efficiently [5]. Nevertheless, the stroke is not fully symmetric, which makes the swimming path somewhat helical. The alga senses variations of light intensity along the helix and controls the stroke of one flagellum in a way that steers the trajectory towards the light source. However, in the absence of light, Chlamydomonas is also able to desynchronize its flagella in order to change its direction of swimming [4]. On a longer time scale, this leads to diffusive motion, which facilitates the cell’s search for better conditions.
Synchronization of cilia and flagella is a ubiquitous phenomenon that occurs between two symmetric flagella on the same organism (like in Chlamydomonas), between flagella of two sperm cells swimming in parallel, or on larger ciliated surfaces, where the beating cilia form so-called metachronal waves. The interaction is hydrodynamic in nature and is not mediated by direct signaling between cilia or flagella. In Chlamydomonas this can be seen in experiments if its two flagella are severed and allowed to re-grow [6]. They will gradually become more synchronized as they grow longer. The exact mechanism of how this synchronization happens is still not well understood.
To better understand how flagella synchronize, Friedrich and Jülicher model the swimming Chlamydomonas cell as three spheres: one representing the body and the other two, the flagella (Fig. 1). Reducing the cell’s complex body shape to three spheres makes it much simpler for the authors to solve the Stokes equation, which governs the low-Reynolds-number flow around the swimmer. They simplify the model still further by neglecting any interactions between the particles, which means assigning each particle a certain drag against the surrounding environment. Although this is a crude approximation, it has worked remarkably well in previous studies of flagellar motion [7].
The authors, surprisingly, find that direct hydrodynamic interactions between the flagella are not necessary for their synchronization. Instead, the two flagella “communicate” with each other through rotation of the body. As long as the flagella beat in phase, the cell swims straight. When they fall out of phase, the motion of one flagellum induces a rocking motion of the cell body, which in turn causes a torque on the other flagellum. In the relevant parameter range, the authors show this torque brings the two flagella back into phase. In a sense, the situation is similar to Huygens’ clocks, which also didn’t interact directly through air, but rather through vibrations in the supporting beam. Using the authors’ model, synchronization between mirror-symmetric flagella beating in opposite directions is surprisingly more robust and easier to explain than the synchronization of cilia beating in parallel. To explain the latter, one needs to take into account higher-order effects [8,9] or more than one degree of freedom per cilium [10].
The above analysis does not imply that hydrodynamic interactions are not important. For instance, without hydrodynamic interactions, no swimmer would be able to perform directed motion [11]. The authors show that only after taking into account interactions can the three-sphere model reproduce the directed swimming of Chlamydomonas. Furthermore, when the body of Chlamydomonas is held clamped in the opening of a micropipette, which prevents the body from rotating, it has been observed that the flagella will still synchronize their strokes [6]. This is something that cannot be explained with the present model, although one may speculate that even a clamped cell still has some elastic compliance that allows for a similar synchronization mechanism.
While this simplified model can explain the experimental observations, we should not forget that a flagellum is a very complex structure. It contains a great variety of motor proteins (dyneins) that are supposed to drive oscillatory and undulatory movements in a cilium or flagellum, but the question on how exactly they generate flagellar or ciliary beats remains open. For a deeper understanding of the role of hydrodynamic interaction on the flagellum’s dynamics, it will be crucial to go beyond a rigid-sphere model and understand its internal mechanics too.
References
- M. Bennett, M. F. Schatz, H. Rockwood, and K. Wiesenfeld, “Huygens’s Clocks,” Proc. R. Soc. London A 458, 563 (2002)
- C. Dobell, Antony van Leeuwenhoek and his “little animals” (Russell and Russell, New York, 1958)
- B. M. Friedrich and F. Jülicher, ”Flagellar Synchronization Independent of Hydrodynamic Interactions,” Phys. Rev. Lett. 109, 138102 (2012)
- M. Polin, I. Tuval, K. Drescher, J. P. Gollub, R. E. Goldstein, “Chlamydomonas Swims with Two “Gears” in a Eukaryotic Version of Run-and-Tumble Locomotion,” Science 325, 487 (2009)
- D. Tam and A. E. Hosoi, “Optimal Feeding and Swimming Gaits of Biflagellated Organisms,” Proc. Natl. Acad. Sci. U.S.A. 108, 1001 (2011)
- R. E. Goldstein, M. Polin, and I. Tuval, “Emergence of Synchronized Beating during the Regrowth of Eukaryotic Flagella,” Phys. Rev. Lett. 107, 148103 (2011)
- B. M. Friedrich, I. H. Riedel-Kruse, J. Howard, and F. Jülicher, “High-Precision Tracking of Sperm Swimming Fine Structure Provides Strong Test of Resistive Force Theory,” J. Exp. Biol. 213, 1226 (2010)
- A. Vilfan and F. Jülicher, “Hydrodynamic Flow Patterns and Synchronization of Beating Cilia,” Phys. Rev. Lett. 96, 58102 (2006)
- N. Uchida and R. Golestanian, “Generic Conditions for Hydrodynamic Synchronization,” Phys. Rev. Lett. 106, 058104 (2011)
- T. Niedermayer, B. Eckhardt, and P. Lenz, “Synchronization, Phase Locking, and Metachronal Wave Formation in Ciliary Chains,” Chaos 18, 037128 (2008)
- A. Vilfan and H. Stark, “Comment on ‘Ferromagnetic Microswimmers’” Phys. Rev. Lett. 103, 199801 (2009)