The Twisted Paths of Bosons

Heiko Rieger

Viewpoint

The Twisted Paths of Bosons

Heiko Rieger

Department of Theoretical Physics, Saarland University, 66123 Saarbrücken, Germany

July 9, 2012• Physics 5, 75

The explanation for why helium doesn’t solidify at low temperatures may be more complicated than previously thought.

Figure caption — **Figure 1:** The “world lines” through time of quantum particles confined to two dimensions can be pictured as soft polymers fluctuating in space. This picture shows the world lines of 8 quantum mechanical particles, which are a) distinguishable boltzmannons and b) indistinguishable bosons. Indistinguishable bosons can “swap” paths with each other, as shown for the 3 blue paths and the 5 green paths. This allows the world lines to become highly entangled without much bending. Boninsegni *et al.* have shown that the highly entangled nature of bosonic world lines is important for explaining why a liquid of helium- $4$ atoms, which are bosons, doesn’t solidify.

Under their own vapor pressure, all known liquids eventually freeze into a crystalline state if they are cooled to sufficiently low temperatures. The exception is helium- $4$ , which crystallizes below $2$ degrees kelvin only at the much higher pressure of $25.3$ bar. (The pressure needed to induce crystallization is approximately independent of temperature down to $0$ kelvin.) According to conventional wisdom, the reason liquid helium doesn’t crystallize at low temperature is that helium atoms are so light that their quantum-mechanical zero-point motion overwhelms the weak interaction between them. In a theoretical paper in Physical Review Letters, Massimo Boninsegni of the University of Alberta in Canada and colleagues [1] show this zero-point motion argument isn’t enough to explain why helium- $4$ doesn’t crystallize at low pressure. Instead, the fact that helium- $4$ atoms are bosons and thus, in contrast to classical particles, indistinguishable, also impedes the formation of crystalline helium. Boninsegni et al.’s work illuminates the general role of Bose statistics in crystallization and emphasizes its importance in determining the phase diagram of helium- $4$ and other systems consisting of interacting bosonic particles.

In contrast to classical particles, which can be labeled and thus distinguished, quantum mechanical particles are indistinguishable. The quantum mechanical wave function that describes two identical bosons must be symmetric with respect to the variables describing each particle; that is, if the variables for particle $1$ and particle $2$ are swapped, the wave function describing the two particles stays the same. A convenient way to visualize this symmetry is to use Feynman’s path integrals, which makes an analogy between the quantum mechanics of a particle and the fluctuations of a peculiar type of classical polymer [2]. In this picture, several quantum particles are like a bunch of floppy spaghetti.

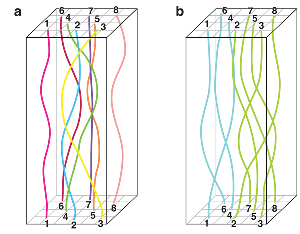
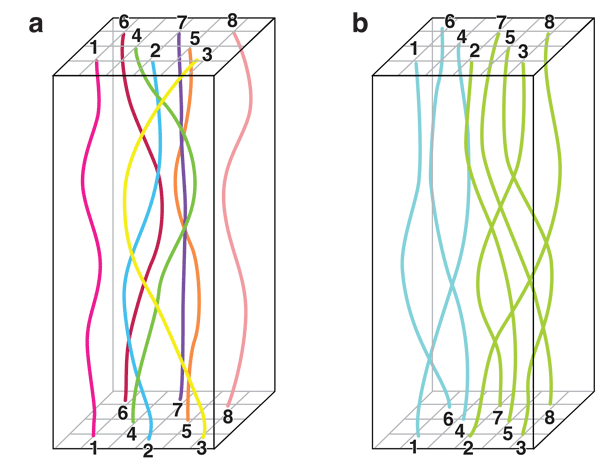
The polymer analogy is helpful for calculating a system of quantum particles’ partition function—a sum over the allowed states, weighted by their energy, which is used in the calculation of thermodynamic quantities and phase diagrams. Formally, the partition function of a $d$ -dimensional, quantum mechanical, many-particle system of bosons is identical to the partition function of a system of soft polymers confined to a ( $d + 1$ )-dimensional box of height $1 / T$ , where $T$ is the temperature of the original quantum system (Fig. 1). This classical partition function is computed by integrating over all possible configurations or arrangements of polymers, each of which is weighted according to its cost in energy (the more a polymer has to bend, the less the path will be weighted). A peculiar feature of this configuration space is that it must have periodic boundary conditions in the height direction in order for the polymer problem to map to the quantum one, which means that polymer positions within the bottom and top plane of the box have to be identical, as sketched in Fig. 1. This is why the distinguishability of the particles is important: If the original quantum mechanical particles are distinguishable (Boninsegni et al. call such particles boltzmannons [1]), then, in the polymer picture, each polymer has to enter and exit at the same point in the bottom and top side, respectively (see Fig. 1(a)). But, if the original quantum mechanical particles are bosons, the entry and exit points of a polymer can be different, yielding polymer configurations that wrap around the box several times, called exchange cycles. All these configurations with arbitrary exchange cycles have to be considered in the path integral for bosons, which means they have a larger configuration space than boltzmannons do.

Boninsegni et al. [1] emphasize that it is exactly this greater freedom for bosonic paths that not only gives rise to superfluidity at low temperatures (hallmarked by the emergence of macroscopic exchange cycles [2]) but also prevents the crystallization of helium- $4$ . Highly entangled configurations of the world lines are representative of the liquid state. Now, the condition that each world line of a boltzmannon, after arbitrary excursions on its way from the bottom to the top, has to return to its entry coordinates causes extra bending energy, so the highly entangled (liquid) world line configuration is less favorable for a system of boltzmannons than it is for a system of bosons. The prediction from this argument is that boltzmannons, with the mass and interatomic potential of helium- $4$ atoms, would crystallize at low temperature and low pressure, whereas bosons with the same parameters would not. Because bosonic world line configurations can be highly entangled without much bending energy they stay highly entangled, and thus liquid, down to zero temperature.

To support this conclusion, the authors search numerically for the liquid-solid phase transition of helium- $4$ atoms for the (fictitious) case where the atoms are distinguishable particles and for the case that the atoms are bosons. Their numerical simulations of both systems are based on the path-integral Monte Carlo method [3], which maps the quantum systems onto classical polymers as mentioned above. By analyzing the world line configurations of the same many-particle system at the same temperature and density—assuming one system consists of boltzmannons, the other of bosons—Boninsegni et al. could clearly demonstrate that the boltzmannons crystallize, whereas the bosons do not.

The calculations have implications for understanding the properties of interacting Bose systems. Neglecting the Bose statistics by not accounting for the way world lines can swap paths—or perform “exchange cycles”—results in an incorrect characterization of the physics of the system and may lead to inaccurate predictions of phase boundaries. Moreover, Boninsegni et al. point out that long exchange cycles are also crucial for determining the lifetime and metastability of the superglass phase of helium- $4$ , which is a metastable amorphous solid, featuring superfluidity [4]. This phase is predicted to occur when helium- $4$ is quenched from high to low temperatures; depending on the initial state of the helium, highly entangled particle world lines may jam. On the one hand, such a state has frozen structural disorder on a microscopic scale; on the other hand, it can support dissipationless flow of its own particles if macroscopic exchange cycles extend throughout the system. In order to find the true equilibrium state, world lines would have to disentangle from these macroscopic exchange cycles, but this is impeded by a free-energy barrier that is higher for bosons than for boltzmannons. Thus Bose statistics appear to stabilize the theoretically predicted super glass phase [4].

Correction (10 July 2012): The original article incorrectly stated that Boninsegni et al. predict boltzmannon helium-4 atoms would crystallize at zero temperature. The statement has been corrected to say their predictions apply to “low temperatures.”

References

M. Boninsegni, L. Pollet, N. Prokof’ev, and B. Svistunov, ”Role of Bose Statistics in Crystallization and Quantum Jamming,” Phys. Rev. Lett. 109, 025302 (2012)
R. P. Feynman, ”Atomic Theory of the $λ$ Transition in Helium,” Phys. Rev. 91, 1291 (1953)
D. M. Ceperley, ”Path Integrals in the Theory of Condensed Helium,” Rev. Mod. Phys. 67, 279 (1995)
M. Boninsegni, N. Prokof’ev, and B. Svistunov, ”Superglass Phase of {4}He,” Phys. Rev. Lett. 96, 105301 (2006)

About the Author

Heiko Rieger received his Dr. rer. nat. from the University of Cologne, Germany, 1989. After postdocs in College Park, Maryland, and Santa Cruz, California, he was a Heisenberg Fellow at the Jülich Research Centre. In 1999 he became full professor for theoretical physics at Saarland University. He has been a visiting professor at Tokyo Metropolitan University (2003), Ecole Normale Supérieure, Paris, (2006), and Université Paris Sud (2009). He works on the statistical physics of nonequilibrium systems (quantum, classical, and biological), disordered materials, and quantum phase transitions.