Taking the Pulse
Periodic oscillations, from a heartbeat to the hum of an electric transformer, are all around us. One ubiquitous phenomenon that occurs when two or more oscillators interact is mutual synchronization: Despite their inevitable differences, oscillators lock to one another and oscillate together at exactly the same frequency. Examples include the synchronization, observed by Huygens, of two clocks ticking on his bedroom wall, the synchronous flashing of fireflies, circadian rhythms, or the seemingly spontaneous transition to synchronous clapping that sometimes occurs in audiences.
Synchronization is of particular relevance in neuroscience: The synchronous firing of groups of neurons is sometimes beneficial for the brain’s information processing, but it can also be detrimental, for example, during an epileptic seizure. A number of models have been proposed to explain the transition to synchrony, but many are too complex to analyze mathematically, or they rely on approximations that make them poor representations of biological reality. Now, writing in Physical Review X, Diego Pazó at the Institute of Physics of Cantabria (CSIC-UC) and Ernest Montbrió at Pompeu Fabra University, both in Spain, show that the Winfree model, a seminal synchronization model, can be analyzed exactly, under certain assumptions [1]. The result could allow the theoretical study of a broad class of oscillators, in particular those that interact through short pulses, the most common case in biology.
In the 1960s, Arthur Winfree proposed his mathematical model, motivated by the desire to understand the synchronization of biological oscillators [2]. One of his key insights was to represent the state of an oscillator by a single angular variable, the phase, which, varying from to , describes the oscillator’s progress along its cycle. This representation considerably simplified the description of a network of oscillators. Winfree’s model contained two functions: a “phase response curve” (describing how an oscillator’s dynamics depend on its own phase) and another function that captures how each oscillator is influenced by the collective rhythm of the others. This second function crucially replaces couplings with a single coupling to a mean field—mathematically, this amounts to a mean-field approximation. The formalism led Winfree to a remarkable discovery: Under certain conditions, the oscillator network undergoes a macroscopic transition to a synchronized state, reminiscent of a phase transition in statistical mechanics.
Unfortunately, his model is too complex to tackle mathematically. Up until now, only in special cases of the two functions could a network of Winfree oscillators be analyzed. The interest soon turned to the easier model proposed by Kuramoto [3], which can be perturbatively derived from the Winfree model. Kuramoto introduced a further simplification: If oscillators interact weakly and are nearly identical, the rate of change of an oscillator’s phase depends only on the difference between its phase and those of all oscillators that influence it. In such a representation, only one function, instead of two, is required to describe the system dynamics. It is this simplification that allows an analytical derivation of the onset of synchronization for Kuramoto-like networks. This elegant result formed the basis of many more investigations and made the Kuramoto formalism the paradigmatic model for describing synchronization phenomena [4].
However, many issues remained unclear for Kuramoto’s model. For example, even though the existence of a synchronized state could be shown mathematically, it was difficult to prove whether this state was actually stable (i.e., could be observed in a real system). These problems were largely solved by a recent result of Ott and Antonsen [5]. They discovered that certain classes of phase oscillator networks, for which mutual coupling is described by a sinusoidal function of phase differences, can be exactly described by a small number of differential equations governing a macroscopic “order parameter.” In essence, they showed that for large networks the probability of an oscillator having a particular phase can be parametrized by a few variables. Remarkably, one can easily derive for such variables a small number of equations (two in the case of the Kuramoto model) that completely describe the behavior of the entire network of oscillators. This process is analogous to modeling the overall motion of a liquid with a few equations, rather than describing the state of each molecule of the liquid.
Pazó and Montbrió have now shown that the original Winfree model can also be analyzed using the Ott-Antonsen approach. This opens up the possibility of extending many of the recent results obtained on Kuramoto-like networks to networks of more general, and biologically realistic, Winfree oscillators. Kuramoto-like networks are less realistic than Winfree ones as they cannot accurately model pulsatile interactions. In contrast, a key advantage of the Winfree model is that its two functions have a biological meaning. The phase response curve can be measured experimentally [6] or derived numerically for an arbitrary oscillator. Pazó and Montbrió use a sinusoidal phase-response function, which is key to their result. The second function is pulselike and determines the influence of an oscillator on others. The authors choose this to be a family of functions described by a single parameter that represents the temporal width of these pulses. The connection of both functions with real biological quantities thus narrows the gap between abstract computer models and networks of, for example, neurons.
The new formalism allowed the authors to explore the synchronization properties of different shapes of the pulses that couple an oscillator network—an aspect that could not have been tackled by Kuramoto-type models. One interesting result they obtain is that narrower pulses (much shorter than the oscillators’ period) have better synchronization properties than broader pulses: They can synchronize more heterogeneous networks, i.e., networks in which the differences between individual oscillators are more pronounced. This may explain why narrow pulses, from the spike of a firing neuron to the flash of a firefly, are ubiquitous in nature.
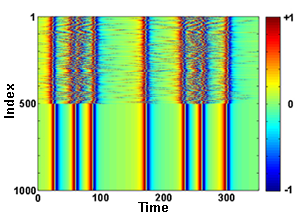
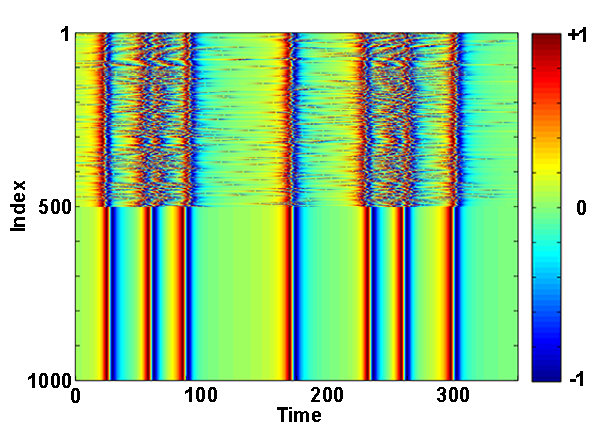
As another demonstration of the capabilities of their approach, Pazó and Montbrió analyze chimera states in a network of two coupled populations of Winfree oscillators (see Fig. 1). Such states have previously been seen in Kuramoto-type models [7] and more recently in real-world physical systems [8]. In this surprising state (whose name derives from mythological chimeras—creatures made of parts of different animals), one population of oscillators synchronizes while the other remains partially incoherent, despite the fact that both populations are identical. Such states have been proposed to explain unihemispheric sleep in dolphins and other animals: The sleeping side of the brain is in sync, while the awake part shows desynchronized activity. The authors show that chimera states also exist in the more realistic Winfree-type networks and deliver a new result: the existence of a chaotic chimera state. In such a state, even though oscillators in one population are perfectly synchronized with one another, their dynamics are not periodic but instead follow a seemingly random trajectory that never repeats itself.
The analysis of coupled oscillator networks remains a hot topic, of relevance not only to mathematicians but also to biologists, physicists, and engineers. Pazó and Montbrió clearly show that networks of Winfree oscillators are now ripe for analysis, and it will be interesting to see what new types of dynamics can occur in them, given their greater generality and closer connection to reality. One promising area of application is computational neuroscience, since their model is closely related to the network of “theta neurons” recently studied by Luke et al. [9]. (A theta neuron is the simplest model able to represent approximately of neurons in the brain.) While neither Ref. [9] nor Ref. [1] consider spatially extended networks, the results by Pazó and Montbrió may allow an important conclusion that still remains elusive [10]: the rigorous derivation, from a discrete 3D network of spiking neurons, of accurate neural field models—macroscopic continuum representations of the cortex that have proven very useful in understanding a diverse range of neural phenomena, from epilepsy to visual hallucinations, but are so far obtained empirically or under a number of unrealistic assumptions.
References
- Diego Pazó and Ernest Montbrió, “Low-Dimensional Dynamics of Populations of Pulse-Coupled Oscillators,” Phys. Rev. X 4, 011009 (2014)
- A. T. Winfree, “Biological Rhythms and the Behavior of Populations of Coupled Oscillators,” J. Theor. Biol. 16, 15 (1967)
- Y. Kuramoto, Chemical Oscillations, Waves, and Turbulence (Springer-Verlag, Berlin, 1984)[Amazon][WorldCat]
- J. Acebron, L. Bonilla, C. Perez Vicente, F. Ritort, and R. Spigler, “The Kuramoto Model: A Simple Paradigm for Synchronization Phenomena,” Rev. Mod. Phys. 77, 137 (2005)
- E. Ott and T. M. Antonsen, “Low Dimensional Behavior of Large Systems of Globally Coupled Oscillators,” Chaos 18, 037113 (2008)
- N. W. Schultheiss, A. A. Prinz, R. J. Butera, Phase Response Curves in Neuroscience: Theory, Experiment, and Analysis (Springer, New York, 2011)[Amazon][WorldCat]
- D. M. Abrams, R. Mirollo, S. H. Strogatz, and D. A. Wiley, “Solvable Model for Chimera States of Coupled Oscillators,” Phys. Rev. Lett. 101, 084103 (2008)
- E. A. Martens, S. Thutupalli, A. Fourrire, and O. Hallatschek, “Chimera States in Mechanical Oscillator Networks,” Proc. Natl. Acad. Sci. U.S.A. 110, 10563 (2013)
- T. B. Luke, E. Barreto, and P. So, “Complete Classification of the Macroscopic Behavior of a Heterogeneous Network of Theta Neurons,” Neural Comput. 25, 3207 (2013)
- C. R. Laing and C. Chow, “Stationary Bumps in Networks of Spiking Neurons,” Neural Comput. 13, 1473 (2001)