Building the Devil’s Staircase
Crystal experts don’t count the way the rest of us do. To them, a perfect quartz crystal with twelve smooth facets counts as only a two faceted crystal, because the rest are related by symmetry. The most complicated crystals produced in labs have at most six types of facets. But in the 13 March PRL a team describes crystals of a “rigid gel” with 60 different facet types, confirming for the first time a prediction from the 1950s, that under ideal conditions, a crystal can show an almost unlimited number of facets on its surface. The work confirms detailed theories on how facets form–a difficult theoretical problem that was solved only recently, and one that is related to other areas of condensed matter physics.
Condensed matter physicists have often wondered why crystals form facets at all. Despite the atomic-scale order of crystals, they could simply form into rounded droplets at the macroscopic scale, as liquids do. But crystals do form facets, and not only in directions parallel to the simplest atomic planes. A crystal with cubic symmetry, for example, can form a facet at 45 degrees to the crystal axes by creating a “staircase” at the atomic scale which moves one crystal unit vertically for each horizontal unit–a facet with “Miller indices” of (110). A much less stable facet with indices (190) would make a very shallow angle with the main axes, proceeding one vertical for every nine horizontal unit cell steps.
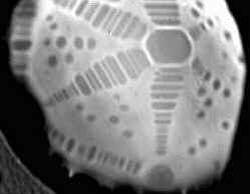
In the 1950s the eminent Russian physicist Lev Landau theorized that in principle, at zero temperature, facets with any Miller indices could form on the surfaces of a crystal, even those at exceedingly shallow inclinations (high Miller indices). The possibility of facets made from staircases at all angles was later dubbed “the Devil’s staircase,” and more comprehensive theories in the 1980s bore out the prediction, even at nonzero temperature. But for most crystals, only a few facets were expected to be stable above the very lowest temperatures. Now Pawel Pieranski and his colleagues at the Paris-Sud University in Orsay, France, have made a type of soap-and-water crystal that can form many stable facets, even at room temperature.
Under the right conditions of temperature, humidity, and concentration, the soapy surfactant molecules form a complex, interpenetrating network with cubic symmetry, and this type of liquid crystal has mechanical properties that can stabilize even very tenuous facets. The Orsay team deposited 1-mm-wide drops of the solution onto a glass surface in a humidity-controlled chamber. By increasing the humidity they coaxed the fluid to form crystals, which they examined with a microscope. They identified at least 60 different facets, including Miller indices as high as 11. The team used laser interferometry to measure the angles of some facets precisely, while others were identified from the geometry.
“The experimental technique is very clever,” says Sebastien Balibar of the École Normale Supérieure in Paris. “I think it’s spectacular that a mixture of soap and water can show at room temperature so many facets that one can test this theory.” The crystal shape problem–which results in the Devil’s staircase–is one of “commensurability,” and amounts to finding the angles at which you can build a staircase if you must completely tile the surface without breaking any tiles, Balibar says. He points out that commensurability comes up in many other problems in condensed matter physics. But the most important reason he and others are interested in the phenomenon is that “we are all interested in the shapes of Nature.”


