New Orbits for Three Bodies
Two objects responding to their mutual gravitational attraction adopt simple elliptical orbits for a wide range of initial conditions. But add one more object and things get complicated and generally defy simple mathematical description. One special case, in which the three bodies rotate as a fixed triangle, was identified by Lagrange two centuries ago. But it was not until the 1970s and the 1990s that researchers found two other families of periodic three-body motion.
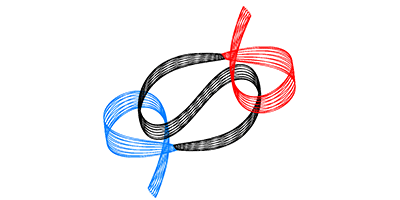
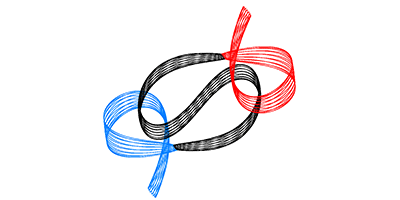
Now, in Physical Review Letters, Milovan Šuvakov and Veljko Dmitrašinović of the Institute of Physics Belgrade, Serbia, have discovered new families of periodic orbits for three equal masses moving under gravity in a plane. To classify these orbits, which were revealed by numerical simulations, Šuvakov and Dmitrašinović extended a previous analysis in which the evolving shape of the triangular arrangement is mathematically represented by a point on a sphere. The physical orbits correspond to closed paths on the sphere, which avoid so-called “collision” points that correspond to two bodies being in the same place. Using this topological classification scheme, the authors were able to distinguish various orbits by the number of times they wind clockwise and counterclockwise around the forbidden points. Of the new families of periodic motion they found, three are related to previous solutions, but ten fall into three entirely new classes. (A gallery of the trajectories is on display here).
The complex motions are hard to visualize, and these orbits would only occur in nature for specific starting conditions. But these special solutions could help researchers better understand the surprisingly complex three-body problem. – Don Monroe