Discrepancy in Neutron Lifetime Still Unresolved
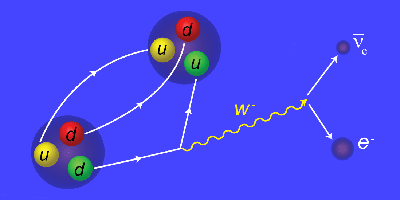
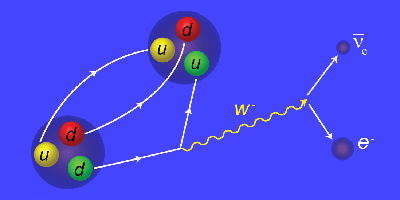
Outside of the nucleus, the proton remains stable for at least years, but an isolated neutron survives just minutes before it decays into a proton, electron, and an antineutrino. Astrophysicists rely on a precise value of the free neutron lifetime to calculate the rate of nucleosynthesis during the big bang, while particle physicists use it to constrain fundamental parameters of the standard model. Yet measured lifetimes have varied by about a percent, depending on the experimental technique. As reported in Physical Review Letters, the latest refinement of the neutron lifetime in one type of experiment has left this discrepancy unresolved.
Researchers have relied on two experimental strategies to measure the neutron lifetime. In the “bottle” method, low-energy neutrons are confined in a trap constructed from magnetic fields or wall materials like beryllium that reflect neutrons. The neutron lifetime can be determined by simply counting the number of particles that survive after a fixed storage time. The alternative is the “in-beam” method, in which a beam of neutrons with a precisely known flux travels through a well-defined volume, and the lifetime is determined by counting the number of decay products.
The two types of experiments give a neutron lifetime that differs by seconds (or standard deviations)—a discrepancy that researchers have chalked up to unresolved systematic errors. As a first step, scientists working at the NIST Center for Neutron Research in Gaithersburg, Maryland, have now refined their earlier in-beam measurement from 2005 with a more accurate value of the neutron flux (the largest uncertainty in the original experiment) by recalibrating their original neutron detector. The NIST researchers now report an in-beam neutron lifetime of , in agreement with their previously measured value, but raising the significance of the discrepancy to standard deviations. – Kevin Dusling
Correction (2 December 2013): Paragraph 3, sentence 1, “2.9 standard deviations” changed to “2.6 standard deviations.”