Getting a handle on difficult atoms

Hendrick L. Bethlem

Viewpoint

Getting a handle on difficult atoms

Laser Centre Vrije Universiteit, de Boelelaan 1081, NL-1081 HV Amsterdam, The Netherlands

September 29, 2008• Physics 1, 25

Paramagnetic atoms and molecules experience a force in a magnetic field and scientists have now used this force to decelerate and trap hydrogen atoms. This method promises new opportunities for precision measurements on hydrogen isotopes and may be applied to a host of atoms and molecules for which existing cooling techniques fail.

Figure caption — **Figure 1:** (Top) Schematic of the Zeeman decelerator and trap. A beam of hydrogen atoms is produced by expanding a gas into vacuum. The hydrogen atoms pass through a small hole into a second vacuum chamber and are decelerated using 12 coils that produce a strong, 2.2 T magnetic field. The atoms come to a near standstill between the last two coils and are subsequently trapped. (Bottom) Periodic table of elements with the maximum effective magnetic dipole of ground-state atoms (in Bohr magnetons) [15] divided by their mass (in amu). For the noble gases this number is also given for the metastable triplet state. The color coding indicates the number of stages required to bring atoms to rest in a setup similar to that used by Hogan *et al.* Atoms that can be brought to rest with less than 100 stages are in yellow and atoms that require more than 400 stages are in red.

Atoms and molecules are said to be paramagnetic when they have one or more unpaired electrons—this is the case for almost all ground-state atoms and many ground-state molecules. The motion of these unpaired electrons around the atomic core gives the atoms a magnetic dipole moment. Scientists can use this magnetic dipole moment as a handle to manipulate the motion of atoms. Now, as reported in Physical Review Letters, S. D. Hogan, A. W. Wiederkehr, H. Schmutz, and F. Merkt at the ETH in Zurich have successfully trapped hydrogen atoms by this means [1], thus opening the way for cooling and trapping a much larger range of atoms than before.

The first manipulation of this kind dates back to the 1920s when Otto Stern and Walther Gerlach performed the experiments that made them famous overnight [2]. In their experiments, Stern and Gerlach passed a collimated beam of silver atoms through a magnetic field that had a strong gradient perpendicular to the beam path. The force exerted on the atoms in the magnetic field is expressed as $F = \cos (θ) μ \nabla B$ , with $θ$ being the angle between the magnetic dipole moment $μ$ and the magnetic field $B$ . If the magnetic moment lies parallel to the magnetic field, the atom experiences a force towards a higher magnetic field strength, and vice versa, if the magnetic moment lies antiparallel to the magnetic field it experiences a force towards a lower magnetic field strength.

Naively, one might expect the dipoles to be randomly oriented when they enter the magnetic field. Following this assumption, one would then expect that the amount that the atoms are deflected should also be random. However, the silver atoms in Stern and Gerlach’s experiment were either deflected towards higher magnetic fields by some amount or were deflected towards lower magnetic fields by that same exact amount. This proved that the angle between the magnetic moment and the magnetic field can in fact only have discrete values, as was predicted earlier by—the then very young—quantum theory. This phenomenon became known as space quantization.

Besides testing quantum theory and boggling the minds of physicists, space quantization has a very interesting practical consequence: If the angle between the magnetic dipole moment and the magnetic field remains fixed, we can introduce an “effective” magnetic dipole moment, $μ_{e f f} = \cos (θ) μ$ . The force on the atom can then simply be written as $F = μ_{e f f} \nabla B$ .

We see that there is a great similarity between the force on a paramagnetic atom in an inhomogeneous magnetic field and the force on a charged particle in an electric field. Thus paramagnetic atoms can be manipulated using inhomogeneous magnetic fields, in the same manner as charged particles can be manipulated using electric fields. Specifically, paramagnetic atoms can be decelerated and trapped using inhomogeneous magnetic fields.

Suppose we let a paramagnetic atom fly into a magnetic field produced by a short solenoid. If the magnetic moment of the atom is oriented antiparallel to the magnetic field, the atom will decelerate while entering the solenoid. If we do nothing, the atom will accelerate while leaving the solenoid. However, if we rapidly switch off the magnetic field while the atom is inside the solenoid, the atom will remain at its lower velocity. By using many solenoids in a series, this process can be repeated until the atom is brought to a near standstill. As the energy that is taken from an atom is equal to the Zeeman shift (that is, the atomic energy level shift caused by the magnetic field), the deceleration process is referred to as Zeeman deceleration. A Zeeman decelerator is the magnetic analog of a linear accelerator (in which charged particles are pushed along by electric fields) or a Stark decelerator for polar molecules (which uses electric-field induced energy level shifts for deceleration) [3,4].

Although the concept of a Zeeman decelerator might be straight forward, the experimental realization is not. In order to have significant velocity loss per stage, the magnetic fields must be very high. At the same time, these fields must be switched on and off within a few microseconds. Combining these two requirements poses a huge challenge. In 2005, Frédéric Merkt at the ETH in Zürich, together with his post-doc Nicolas Vanhaecke—who had previously worked with Stark decelerators—took on this challenge. Shortly after, they were followed by a group at the University of Texas at Austin led by Edvardas Narevicius and Mark Raizen in collaboration with Uzi Even from Tel-Aviv University in Israel, who specializes in switching high magnetic fields for making pulsed molecular beam nozzles.

Merkt and co-workers first demonstrated Zeeman deceleration in 2006, initially using six [5,6], and later twelve [7], pulsed magnetic field stages to slow down beams of H and D atoms. Raizen and co-workers used a decelerator initially consisting of 18 [8], and later 64 [9], stages to decelerate metastable neon atoms. Earlier this year Raizen and co-workers also reported the deceleration of oxygen molecules [10]. The trapping of hydrogen atoms that has now been reported by Stephen Hogan and co-workers [1] heralds a major breakthrough.

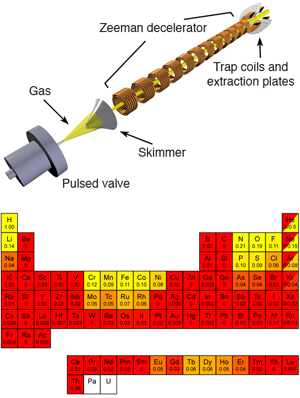
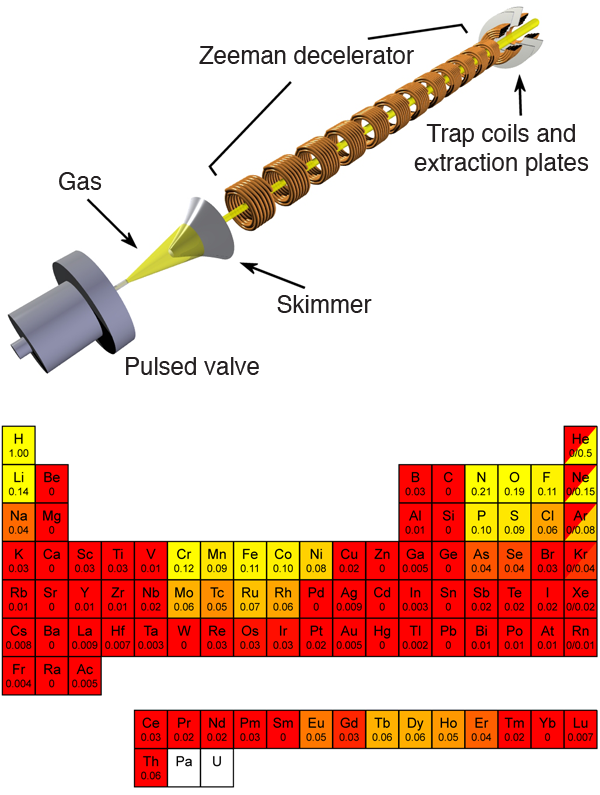
The experimental setup used by Hogan et al. is shown in Fig. 1 (top). A cloud of ammonia molecules is released and photodissociated using UV light to create a beam of hydrogen atoms. The hydrogen atoms have an initial velocity of 520 m/s, and are decelerated to 100 m/s using twelve coils that create a magnetic field of 2.2 T on the axis. The atoms are brought to a standstill in between the last two coils. At that time, opposite currents are run through the last two solenoids. This results in a magnetic field strength that is zero on the axis at the midpoint between the two coils, and increases away from this point. Atoms that have their magnetic moment oriented antiparallel to the magnetic field will be attracted to the magnetic field minimum and, if slow enough, will remain trapped. Hogan et al. estimate that the temperature of the trapped hydrogen atoms is on the order of 100 mK.

Although different elements, including hydrogen, have previously been trapped, the experiment by Hogan et al. marks an important advance. Until now, mostly laser cooling has been used as a first step to trap atoms. However, laser cooling requires a particular level structure that excludes many atoms and all molecules. In contrast, Zeeman deceleration requires only a sufficiently large magnetic moment in the atom or molecule under investigation. In the periodic table at the bottom of Fig. 1, the value for the effective magnetic moment (in Bohr magnetons) divided by their mass (in amu) is given for selected ground-state atoms. This number determines how many magnetic deceleration stages are needed to bring a certain element to (near) rest. In the experiment of Hogan et al., 12 stages were used to decelerate and trap hydrogen. It follows that in order to trap, for instance, phosphorous atoms, one needs 120 magnetic field stages similar to those used by Hogan et al. Thus a machine consisting of 200 magnetic deceleration stages would make the trapping of 19 different elements possible. Such a machine would also be able to decelerate many molecules such as $O_{2}$ [10], $NO$ , $OH$ , and $NH$ . If one is willing to build a machine consisting of 400 stages, the number of elements that can be trapped increases to 31.

The fact that hydrogen has been trapped is especially noteworthy. Hydrogen, the simplest and most well-understood atom, permits unique confrontations between experiment and theory [11]. Whereas the helium dilution refrigerators that have been used so far to trap hydrogen [12] are bulky complicated machines with limited flexibility and (optical) access, Zeeman decelerators have no such limitations. Moreover, a Zeeman decelerator will work equally well with deuterium and tritium atoms (save for a factor of two or three more stages to compensate for the larger mass of deuterium or tritium, respectively). Trapped tritium atoms might offer a novel approach for studying the beta decay of tritium and for measuring the (as yet unknown) mass of the electron neutrino [13]. Even more speculative, Zeeman deceleration might prove useful for decelerating and trapping antihydrogen. This would make it possible to test with utmost precision if there are differences between matter and antimatter—even a tiny difference would require scientists to reformulate the most basic laws of physics [14].

Note added by author (20 January 2009): In my Viewpoint “Getting a handle on difficult atoms,” I described the development of Zeeman deceleration from my perspective. My wording in the sentence “Shortly after (Vanhaecke and Merkt started their experiments), they were followed by a group at the University of Texas in Austin led by Edvardas Narevicius and Mark Raizen…” was somewhat ambiguous. I wish to emphasize that, although Merkt and co-workers [5] (submitted 30 November 2006) demonstrated Zeeman deceleration before Raizen and co-workers [8] (submitted 10 September 2007), to the best of my knowledge, both groups pursued this direction in parallel and completely independently.

References

S. D. Hogan, A. W. Wiederkehr, H. Schmutz, and F. Merkt, Phys. Rev. Lett. 101, 143001 (2008)
W. Gerlach and O. Stern, Z. Physik 9, 349 (1922)
H. L. Bethlem, G. Berden, and G. Meijer, Phys. Rev. Lett. 83, 1558 (1999)
S. Y. T. van de Meerakker, H. L. Bethlem, and G. Meijer, Nat. Phys 4, 595 (2008)
N. Vanhaecke, U. Meier, M. Andrist, B. H. Meier, and F. Merkt, Phys. Rev. A 75, 031402 (2007)
S. D. Hogan, D. Sprecher, M. Andrist, N. Vanhaecke, and F. Merkt, Phys. Rev. A 76, 023412 (2007)
S. D. Hogan, A. W. Wiederkehr, M. Andrist, H. Schmutz, and F. Merkt, J. Phys. B: At. Mol. Opt. Phys. 41, 081005 (2008)
E. Narevicius, C. G. Parthey, A. Libson, J. Narevicius, I. Chavez, U. Even, and M G Raizen, New J. Phys. 9, 358 (2007)
E. Narevicius, A. Libson, C. G. Parthey, I. Chavez, J. Narevicius, U. Even, and M. G. Raizen, Phys. Rev. Lett. 100, 093003 (2008)
E. Narevicius, A. Libson, C. G. Parthey, I. Chavez, J. Narevicius, U. Even, and M. G. Raizen, Phys. Rev. A 77, 051401 (2008)
T. W. Hänsch, Rev. Mod. Phys. 78, 1297 (2006)
H. F. Hess, G. P. Kochanski, J. M. Doyle, N. Masuhara, D. Kleppner, and T. J. Greytak, Phys. Rev. Lett. 59, 672 (1987)
E. Narevicius, C. G. Parthey, A. Libson, M. F. Riedel, U. Even, and M. G. Raizen, New J. Phys. 9, 96 (2007)
G. Gabrielse, Adv. Atom. Mol. Opt. Phys. 50, 155 (2005)
J. M. Doyle, B. Friedrich, J. Kim, and D. Patterson, Phys. Rev. A 52, R2515 (1995)

About the Author

Hendrick Bethlem graduated from the Vrije Universiteit in Amsterdam in 1997, and completed his Ph.D. at the Radboud University in Nijmegen in 2002. Following post-doctoral research at Imperial College London he became a group leader at the Fritz-Haber-Institut der Max-Planck-Gesellschaft in Berlin. In 2005 he returned to the Vrije University. His research interests include the manipulation of molecules by electric fields and the use of cold molecules for precision tests. His work is funded by the Netherlands Organisation for Scientific Research (NWO) via a VIDI-grant and by the European Research Council via a Starting Grant.