A New Angle on Quantum Impurities
Understanding how impurities interact with a quantum environment is an important problem with widespread implications in physics [1, 2]. An impurity has complex quantum-mechanical interactions with its host environment, and it can acquire properties that differ greatly from those of the impurity in isolation. However, such many-body effects are formidably challenging to describe with theory. A new theoretical approach introduced by Mikhail Lemeshko at the Institute of Science and Technology in Austria [3] provides a simple and elegant way to describe an important type of impurity: a molecule immersed in a quantum solvent. Analyzing experimental data collected by various groups over two decades, Lemeshko has shown that molecules in one such solvent, superfluid helium, form quasiparticles called angulons. This finding may lead to a substantial simplification of theories that describe a broad range of molecules and solvents.
Trapping a molecule in a droplet of a superfluid—a liquid with zero viscosity—is a helpful trick for high-precision spectroscopy. Superfluid helium droplets are inert and ultracold (0.4 K), and they protect the molecule from external perturbations. For instance, the superfluid reduces some of the factors that broaden molecular spectral lines, like collisions or the Doppler effect. This allows researchers to achieve a very high resolution of the narrow rotational lines of the molecules.
However, experiments have shown that a superfluid environment can strongly affect the molecule’s rotation, thereby shifting its spectral lines. For example, the rotational lines of a carbonyl sulfide ( ) molecule in superfluid helium are approximately 3 times more closely spaced in energy than when the molecules are in the gas phase. Since the rotational energies of a molecule are inversely proportional to its moment of inertia, the narrower spacing between lines reveals that the effective moment of inertia of the molecule in superfluid helium is substantially larger. Until now, this strong “renormalization” of the moment of inertia defied a simple analytic description. Instead, to interpret experimental data, researchers have had to run complex numerical simulations that are limited to small helium clusters and simple molecules. Moreover, these simulations often don’t provide an intuitive picture of the underlying physics.
To tackle the problem analytically, Lemeshko followed a paradigmatic approach to describing quantum impurities that has allowed researchers to describe several complicated many-body effects. Such an approach is best illustrated by the description of a conduction electron interacting with the atoms in a solid. When the electron moves in a crystal lattice, surrounding atoms adjust their positions, leading to a local polarization centered on the electron. The exact solution of this problem requires a description of the positions of all the electrons and nuclei in the crystal as well as their interactions, which would involve billions upon trillions of degrees of freedom. Such a situation is intractable by any existing numerical methods. However, many decades ago, Lev Landau and Solomon Pekar resolved this problem by introducing a so-called polaron quasiparticle, which is composed of an electron “dressed” by the local polarization of surrounding media [4, 5]. A polaron behaves like a free electron but with a larger mass and a different mobility and magnetic impedance—renormalized properties whose values depend on the magnitude of the electron-lattice interaction and other microscopic details. The polaron picture has provided insights into the physics of semiconductors, strongly correlated materials, and ultracold atoms [2].
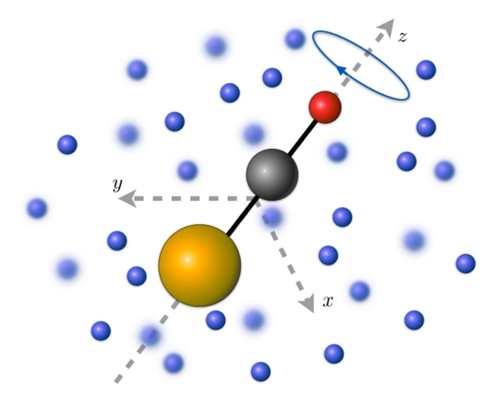
Inspired by the concept of polarons, Lemeshko wondered if a similar quasiparticle approach could simplify the problem of rotating polyatomic molecules interacting with quantum solvents. In 2015, working with Richard Schmidt of Harvard University, Lemeshko proposed such a quasiparticle, the angulon [6]. When a rotating molecule is placed inside a quantum solvent, its motion becomes dressed by the many-body excitations of its environment, leading to the formation of the angulon (see Fig. 1). The interaction redistributes the total angular momentum of the rotating molecule over the molecule and its host. Similar to a polaron, the dressed molecule can then be described in terms of an effective moment of inertia and rotational constant.
Lemeshko has now demonstrated, through a comparison of theoretical predictions and experimental results, that such a quasiparticle approach is particularly helpful for understanding the rotational structure in the absorption spectrum of molecules immersed in quantum solvents, such as superfluid helium [3]. Previously, the theoretical description of this problem required extensive numerical simulations based on first-principle approaches [7]. No analytical solution was possible. In his new work, Lemeshko achieved such a solution by using a variational approach that involves minimizing the energy of the system. This method is based on a wave function that can describe an infinite number of elementary excitations (phonons, maxons, and rotons) in the superfluid helium. This is necessary to describe a regime in which the coupling between the impurity and the solvent is strong. Lemeshko was able to derive, in both the regimes of strong and weak coupling, simple analytical expressions for parameters that describe the molecule in terms of its interaction with the environment.
Using these expressions, the author analyzed a vast set of experimental data on several polyatomic molecules in superfluid helium [8], focusing on their rotational constants, which are inversely proportional to the moment of inertia of the molecules. Lemeshko analyzed data for molecules that interact strongly with the superfluid (e.g., , , and ) and others that interact weakly (e.g., , , and ), finding that in both cases the experimental values of the rotational constants agree well with the values predicted by angulon theory. A numerical solution of the angulon theory is still required to find the rotational constants of molecules that are neither weakly nor strongly interacting (e.g., , , and ). However, the analytical solution for the limiting case of weak (strong) coupling provides a lower (upper) boundary for the experimental value of the molecule’s rotational constant.
The results of this paper are particularly important for the rotational spectroscopy of molecules in helium nanodroplets and degenerate quantum gases, such as Bose-Einstein condensates of ultracold atoms. The angulon theory can be easily applied to large polyatomic molecules and molecular complexes, which are particularly cumbersome to treat with other theoretical approaches. With simple analytical expressions available, analyzing experimental data will be much simpler. This will help researchers use molecules immersed in quantum solvents as remarkably small sensors that are a few atoms in size. Spectroscopic analysis of such sensors could reveal many interesting manifestations of many-body physics on the nanoscale in quantum solvents, including the real-time formation of superfluidity in helium droplets. This sensing technique may also be extended to probe many strongly correlated solvents and systems, such as quasi-1D and quasi-2D ultracold dipolar and quadrupolar gases as well as cold Rydberg atom gases.
This research is published in Physical Review Letters.
References
- A. C. Hewson, The Kondo Problem to Heavy Fermions (Cambridge University Press, Cambridge, 1993)[Amazon][WorldCat].
- D. Emin, Polarons (Cambridge University Press, Cambridge, 2013)[Amazon][WorldCat].
- M. Lemeshko, “Quasiparticle Approach to Molecules Interacting with Quantum Solvents,” Phys. Rev. Lett. 118, 095301 (2017).
- L. D. Landau, “Electron Motion in Crystal Lattices,” Phys. Z. Sowjetunion 3, 664 (1933).
- L. D. Landau and S. I. Pekar, “Polaron Effective Mass,” Zh. Eksp. Teor. Fiz. 18, 419 (1948).
- R. Schmidt and M. Lemeshko, “Rotation of Quantum Impurities in the Presence of a Many-Body Environment,” Phys. Rev. Lett. 114, 203001 (2015).
- K. Szalewicz, “Interplay Between Theory and Experiment in Investigations of Molecules Embedded in Superfluid Helium Nanodroplets,” Int. Rev. Phys. Chem. 27, 273 (2008).
- J. P. Toennies and A. F. Vilesov, “Spectroscopy of Atoms and Molecules in Liquid Helium,” Ann. Rev. Phys. Chem. 49, 1 (1998).