Closing in on a Magnetic Analog of Liquid Crystals

Frédéric Mila

Viewpoint

Closing in on a Magnetic Analog of Liquid Crystals

Institute of Physics, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland

June 12, 2017• Physics 10, 64

Nuclear magnetic resonance measurements strengthen the case that spins in a copper oxide exhibit nematic order similar to that found in liquid crystals.

Figure caption — **Figure 1:** Unlike typical magnets, whose order parameters are vectors, spin-nematic phases have order parameters that are tensors. (Left) In the simplest example of spin-nematic order, spin fluctuations of nonmagnetic spin-1 atoms (only one shown) occur perpendicular to a “director” (red line), breaking rotational symmetry without producing a net magnetization. (Right) Orlova *et al.* have used NMR to observe spin-nematic order in ${LiCuVO}_{4}$ . In this system, the fluctuations are associated with neighboring pairs of spin-1/2 copper ions (purple spheres) and the director alternates between two perpendicular directions.

In 1888, the Austrian chemist Friedrich Reinitzer was trying to measure the melting point of cholesteryl benzoate crystals [1] when, much to his surprise, he observed not one but two phase transitions. Reinitzer had inadvertently discovered liquid crystals. In this cloudy-looking phase, intermittent between a solid and a liquid, the molecules are at random positions but nonetheless break rotational symmetry. The essence of this type of order escaped the physics community until the 1960s, when Pierre-Gilles De Gennes realized that the order parameter describing it could not be expressed as a number (like the density of a gas) or a vector (like the direction of a solid’s magnetization), but only by a more complex mathematical entity: a tensor [2]. Soon after, theorists predicted that a quantum version of a common type of order found in liquid crystals, known as nematic order, might be possible in a lattice of spins [3]. Yet besides being observed in condensates of cold atoms [4], spin-nematic order has remained elusive. Among solids, the most promising spin-nematic candidate today is the copper oxide ${LiCuVO}_{4}$ [5]. Thanks to nuclear magnetic resonance (NMR) measurements performed at high magnetic fields, Anna Orlova of France’s National Laboratory for Intense Magnetic Fields (LNCMI) and colleagues now provide the strongest evidence to date that ${LiCuVO}_{4}$ indeed exhibits a spin-nematic phase [6].

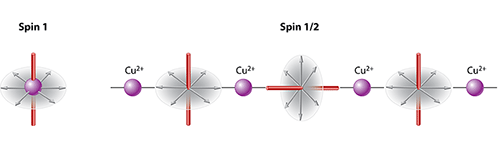
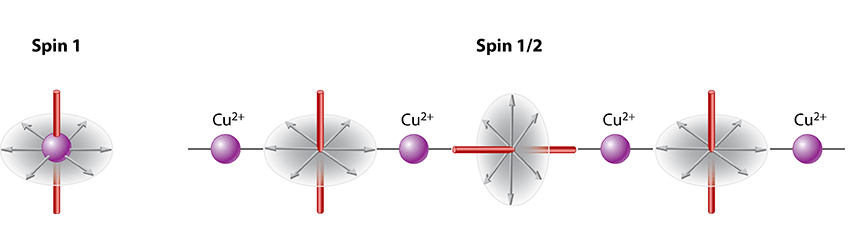
Like liquid crystals, spin systems are predicted to exhibit different types of nematic phases. The simplest example is the quadrupolar phase of a lattice of spin-1 atoms. The projection of a spin 1 atom onto a given direction, say $z$ , can take the values -1, 1, or 0. The value of 0 corresponds to a nonmagnetic atom because the quantum expectation values for the spin magnetic moments along $x$ , $y$ , and $z$ are all zero. However, while the expectation value for spin fluctuations along $z$ also vanishes $(〈 S_{z}^{2} 〉 = 0)$ , those for fluctuations along $x$ and $y$ ( $〈 S_{x}^{2} 〉$ and $〈 S_{y}^{2} 〉$ ) do not (Fig. 1, left). When quadrupolar order sets in, all spins are in this nonmagnetic state and fluctuating perpendicular to a fixed direction known as the director, which can vary from site to site. The order can be stabilized by biquadratic interactions between spins and is defined by an order parameter that is a tensor, not a vector.

A similar nematic phase is also possible for spin-1/2 systems, but the physics is more complicated. Locally, any spin-1/2 atom is magnetic because its spin must point up or down along some direction. To form a spin-nematic phase, the spins must therefore somehow pair up to have a spin of 1. This can occur in an interesting way for spin-1/2 atoms in a magnetic field close to “saturation,” that is, a field strong enough to fully polarize the spins [7]. In this situation, single-spin flips that propagate through the lattice, called magnons, will usually form a condensate, analogous to a Bose-Einstein condensate of atoms. However, magnons can attract one another, and if this attraction is strong enough, they can form bound states that condense before the single magnons do. In this phase, single spin-flip correlations decay exponentially, but correlations between pairs of spin flips are long-ranged. The order parameter for this phase is defined by a product of two spin operators $S_{i}^{+} S_{i + 1}^{+}$ , where $i$ and $i + 1$ are neighboring sites and the $+$ denotes a spin flip. The resulting operator is one of the five components of a rank-2 tensor.

The above scenario is thought to happen in ${LiCuVO}_{4}$ . In this compound, each copper ion has a spin of 1/2 and interacts strongly only with its closest neighbors along one of the crystal axes, thus forming quasi-1D spin chains. For a field just below saturation along an arbitrary direction, say $z$ , the predicted spin ground state [7] is a condensate of bound magnons in which pairs of neighboring spins fluctuate around a director that alternately points along $x$ or $y$ (Fig. 1, right).

The first experimental evidence for this exotic phase in ${LiCuVO}_{4}$ came in 2011, when a team measured the material’s magnetization in a high applied magnetic field. As they lowered the field strength by a few tesla (T) from saturation (which occurs close to 50 T in ${LiCuVO}_{4}$ ), they observed a kink in the magnetization [5]. They interpreted this feature as indicating a transition from a condensate of bound magnons to one of single magnons.

Orlova et al. have taken a significant step towards confirming that the phase above the kink corresponds to spin-nematic order by showing that it is not magnetically ordered perpendicular to the field (see note in Ref. [8]). In other words, this phase cannot be described by a vector and is therefore probably nematic in nature. To do so, the team performed a tour de force NMR measurement, in which they succeeded in determining the resonant frequencies of the compound’s vanadium nuclear spins in fields as high as 55 T by using pulsed fields that lasted a few milliseconds; with today’s technology, steady fields can only reach 45 T. The NMR frequency spectrum is very sensitive to the local magnetic field at the vanadium-ion sites, probing the total external field plus any internal field produced by the magnetic moments of the neighboring copper ions. In a nonmagnetic phase, like that expected for spin-nematic ordering, the internal field is the same at every site, so the NMR spectrum consists of a single line that shifts but does not broaden when changing the applied field. By contrast, if the field induces an ordering of the copper spins, different vanadium sites will be exposed to different local fields and the spectral line will broaden into a shape that’s indicative of the particular magnetic order. Orlova et al. found that, as they decreased the strength of the pulsed magnetic field to just below saturation, a phase appeared in which the vanadium line shifted but did not broaden with respect to the line above saturation—clearly indicating the absence of magnetic order. No broadening was observed until the field was further reduced and a spin-density phase, known from previous experiments, formed.

Despite this progress, Orlova and colleagues’ work doesn’t constitute a definitive proof of spin-nematic order, which would require sensitivity to fluctuations of the two-spin operator that defines the order parameter. The most direct way of doing so would be to use a light-scattering probe such as Raman scattering [9]. Alternatively, spin-nematic order has been shown to have specific consequences on spin relaxation rates, which can be measured with NMR, and on the intensity of the Goldstone modes of that phase, known as quadrupolar waves, which can be detected by neutron scattering [10]. However, performing all of these experiments at the necessarily large magnetic fields would be a real challenge.

This research is published in Physical Review Letters.

References

F. Reinitzer, “Beiträge zur Kenntniss des Cholesterins,” Monatshefte für Chemie 9, 421 (1888).
P.-G. De Gennes, The Physics of Liquid Crystals (Clarendon Press, Oxford, 1974)[Amazon][WorldCat].
M. Blume and Y. Y. Hsieh, “Biquadratic Exchange and Quadrupolar Ordering,” J. Appl. Phys. 40, 1249 (1969); A. F. Andreev and I. A. Grishchuk, “Spin Nematics,” Zh. Eksp. Teor. Fiz. 87, 467 (1984), [Sov. Phys. JETP 60, 267 (1984)].
D. M. Stamper-Kurn and M. Ueda, “Spinor Bose Gases: Symmetries, Magnetism, and Quantum Dynamics,” Rev. Mod. Phys. 85, 1191 (2013).
L. E. Svistov, T. Fujita, H. Yamaguchi, S. Kimura, K. Omura, A. Prokofiev, A. I. Smirnov, Z. Honda, and M. Hagiwara, “New High Magnetic Field Phase of the Frustrated S = 1/2 Chain Compound ${LiCuVO}_{4}$ ,” JETP Lett. 93, 21 (2011).
A. Orlova, E. L. Green, J. M. Law, D. I. Gorbunov, G. Chanda, S. Kramer, M. Horvatic, R. K. Kremer, J. Wosnitza, and G. L. J. A. Rikken, “Nuclear Magnetic Resonance Signature of the Spin-Nematic Phase in ${LiCuVO}_{4}$ at High Magnetic Fields,” Phys. Rev. Lett. 118, 247201 (2017).
M. E. Zhitomirsky and H. Tsunetsugu, “Magnon Pairing in Quantum Spin Nematic,” Europhys. Lett. 92, 37001 (2010); Similar ideas have been put forward earlier in other contexts. See, e.g., A. V. Chubukov, “Chiral, Nematic, and Dimer States in Quantum Spin Chains,” Phys. Rev. B 44, 4693 (1991); and N. Shannon, T. Momoi, and P. Sindzingre, “Nematic Order in Square Lattice Frustrated Ferromagnets,” Phys. Rev. Lett. 96, 027213 (2006).
Previous NMR measurements of ${LiCuVO}_{4}$ by Büttgen et al. did not observe this nonmagnetic phase, perhaps because the experiments were performed on samples with more impurities. N. Büttgen, K. Nawa, T. Fujita, M. Hagiwara, P. Kuhns, A. Prokofiev, A. P. Reyes, L. E. Svistov, K. Yoshimura, and M. Takigawa, “Search for a Spin-Nematic Phase in the Quasi-One-Dimensional Frustrated Magnet ${LiCuVO}_{4}$ ,” Phys. Rev. B 90, 134401 (2014).
F. Michaud, F. Vernay, and F. Mila, “Theory of Inelastic Light Scattering in Spin-1 Systems: Resonant Regimes and Detection of Quadrupolar Order,” Phys. Rev. B 84, 184424 (2011).
A. Smerald, H. T. Ueda, and N. Shannon, “Theory of Inelastic Neutron Scattering in a Field-Induced Spin-Nematic State,” Phys. Rev. B 91, 174402 (2015); A. Smerald and N. Shannon, “Theory of NMR $1 ∕ T_{1}$ Relaxation in a Quantum Spin Nematic in an Applied Magnetic Field,” 93, 184419 (2016).

About the Author

Frédéric Mila is a condensed-matter theorist who studies strongly correlated systems. After completing his Ph.D. in surface physics at the Université Paris Sud, he did postdoctoral research at the ETH in Switzerland, Rutgers University in the U.S., and Université de Neuchâtel, also in Switzerland, studying high-temperature cuprate superconductors and organic conductors. He later took a position with the CNRS in Toulouse, where he stayed until 2000. He is now a professor at the École Polytechnique Fédérale de Lausanne in Switzerland. His current research focus is frustrated magnetism and SU(N) models of cold atoms.