A Roadmap for a Scalable Topological Quantum Computer
The Herculean thrust to realize a quantum computer by many research groups around the world is, in my opinion, one of the most exciting endeavors in physics in quite some time. Notwithstanding the potential applications that have motivated many companies in this endeavor, a quantum computer represents the most promising avenue to peer into quantum phenomena on a macroscopic scale. As with any such great effort, the race to build a quantum computer has many competitors pursuing a variety of approaches, some of which appear to be on the verge of creating a small machine [1]. However, such small machines are unlikely to uncover truly macroscopic quantum phenomena, which have no classical analogs. This will likely require a scalable approach to quantum computation. A new study by Torsten Karzig from Microsoft Station Q, California, and colleagues [2] brings together the expertise of a large and diverse group of physicists, ranging from experimentalists to topologists, to lay out a roadmap for a scalable architecture based on one of the most popular approaches.
Karzig and colleagues’ paper represents a vision for the future of a sequence of developments that started with the seminal ideas of topological quantum computation (TQC) as envisioned by Alexei Kitaev [3] and Michael Freedman [4] in the early 2000s. The central idea of TQC is to encode qubits into states of topological phases of matter (see Collection on Topological Phases). Qubits encoded in such states are expected to be topologically protected, or robust, against the “prying eyes” of the environment, which are believed to be the bane of conventional quantum computation. This is because states of topological phases are locally indistinguishable from each other, so that qubits encoded in such states can evade the destructive coupling to the environment. But experimentally accessible topological phases of matter with the requisite properties for TQC, such as the ability to host quasiparticles known as Majorana zero modes, have been elusive. A milestone in this direction was reached in 2010, when researchers realized [5–7] that the combination of rather conventional ingredients, such as special semiconductors, superconductors, and magnetic fields, could result in one such phase—a topological superconductor. This realization motivated experimentalists to discover signatures of this topological phase just a few years after its prediction [8]. However, the topological superconductors, or Majorana nanowires as they are often called, made in these first experiments were plagued by device imperfections such as impurities [8]. While topological robustness is supposed to protect devices from small imperfections, it is sometimes overlooked that the strength of such imperfections must be below a pretty low threshold for topological robustness to be operative.
A new wave of optimism swept the search for TQC-ready topological superconductors in 2016. That’s when experimental groups from the University of Copenhagen and from the Delft University of Technology, led by Charlie Marcus and Leo Kouwenhoven, respectively, demonstrated high-quality Majorana nanowires that were likely to be in the topological regime [9, 10]. These devices, fabricated through epitaxial growth of superconducting aluminum on indium antimonide semiconductors, showed evidence of a high-quality superconducting gap [10] and also of near energy degeneracy between the topological qubit states [9]; a large energy difference between qubit states is often related to the detrimental decoherence rate of a qubit. However, the rules of the game of designing and fabricating Majorana nanowire devices have proven to be rather different from what had been anticipated. For example, it turns out that it is quite straightforward to drive the newly fabricated devices [9] into the desirable Coulomb blockade regime (where the quantization of electronic charge dominates charge transport) but difficult to fabricate controllable contacts to connect the devices to superconducting circuitry. Interestingly, concurrent theoretical work has clarified that the topological qubit state of a Majorana nanowire can be measured via the phase shift of electron transport through the device when the transport is in the Coulomb blockade regime. This work led to suggestions that the basic operations for TQC could be performed using a procedure that relied on measurements of topological qubits.
Karzig and colleagues’ study comes at a point in time where there is optimism for the realization of TQC using Majorana nanowires but possibly along a path with several constraints. For example, branched structures of a nanowire could be used to generate a network of wires for TQC, but superconducting contacts are only easy to make at the ends of the wire. This would mean that superconducting contacts must be avoided in making a large network of wires. Also, the qubit lifetime will ultimately likely be limited by quasiparticle poisoning, a phenomenon in which an anomalously large number of unwanted quasiparticles, arising from Cooper electron pairs broken by stray microwaves, exists in the devices. The Karzig study brings together a large number of authors with expertise in device fabrication, in strategies for TQC, and in the solid-state-physics issues involving Majorana nanowires. The researchers propose a protocol for scalable TQC based on the existing Majorana nanowires, assuming that they can be brought into the topological phase.
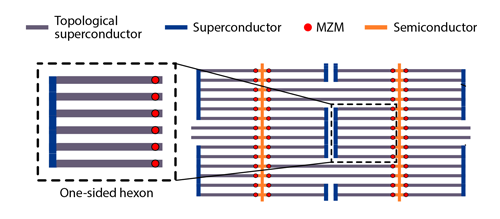
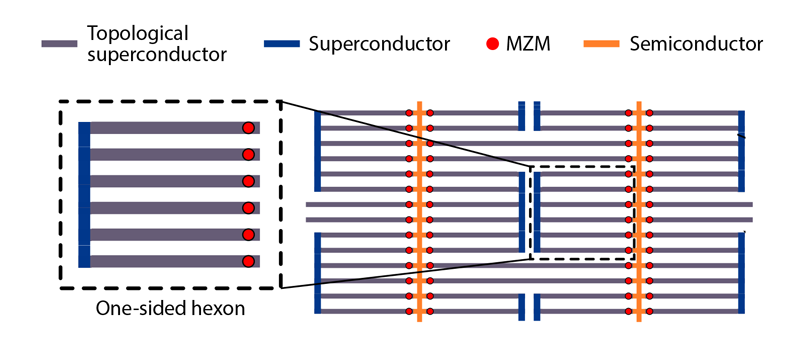
The protocol involves designing a network from small sets of Majorana wires and performing a sequence of measurements on the sets (Fig. 1). The central idea is to use physical constraints on the network, such as aligning all wires with a global magnetic field, to predict which sets may be measured easily to perform TQC. For example, the researchers considered networks made from sets of four and six wires (“tetron” and “hexon” designs) together with the rule that only nearby Majorana zero modes could be measured in each configuration. They then devised a strategy for TQC that optimizes robustness to quantities such as environmental temperature and noise as well the size of the network. The result of the analysis is a few scalable architectures that future experimental groups could pick between, depending on their device-construction capabilities and computational goals. The hexon architectures are likely to be computationally more efficient than the tetron architectures but will probably be more difficult to construct.
While the scope of this work might be limited to these specific devices, detailed analysis of this kind is absolutely key to motivating both experimentalists and theorists to make progress towards a realistic platform for TQC that actually works in practice. The Karzig study likely lays the foundation for analogous work with other topological platforms as they become experimentally viable candidates for TQC. I must also clarify that the significance of this work does depend on whether future experiments meet the outstanding experimental challenges, foremost among which is the reliable generation of Majorana nanowires in a topological phase. That being said, I think Karzig and co-workers’ paper will serve as a case study to follow, even if the properties of topological superconducting systems turn out to be somewhat different from the ones assumed.
This research is published in Physical Review B.
References
- The Economist, “Quantum Leaps,” 11 March 2017.
- T. Karzig et al., “Scalable Designs for Quasiparticle-Poisoning-Protected Topological Quantum Computation with Majorana Zero Modes,” Phys. Rev. B 95, 235305 (2017).
- A. Y. Kitaev, “Fault-Tolerant Quantum Computation by Anyons,” Ann. Phys. 303, 2 (2003).
- M. H. Freedman, “Quantum Computation and the Localization of Modular Functors,” Found. Comput. Math. 1, 183 (2001).
- J. D. Sau, R. M. Lutchyn, S. Tewari, and S. Das Sarma, “Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures,” Phys. Rev. Lett. 104, 040502 (2010).
- R. M. Lutchyn, J. D. Sau, and S. Das Sarma, “Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures,” Phys. Rev. Lett. 105, 077001 (2010).
- Y. Oreg, G. Refael, and F. von Oppen, “Helical Liquids and Majorana Bound States in Quantum Wires,” Phys. Rev. Lett. 105, , 077001 (2010).
- C. W. J. Beenakker, “Search for Majorana Fermions in Superconductors,” Annu. Rev. Condens. Matter Phys. 4, 113 (2013).
- S. M. Albrecht, A. P. Higginbotham, M. Madsen, F. Kuemmeth, T. S. Jespersen, J. Nygård, P. Krogstrup, and C. M. Marcus, “Exponential Protection of Zero Modes in Majorana Islands,” Nature 531, 206 (2016).
- H. Zhang et al., “Ballistic Majorana Nanowire Devices,” arXiv:1603.04069.