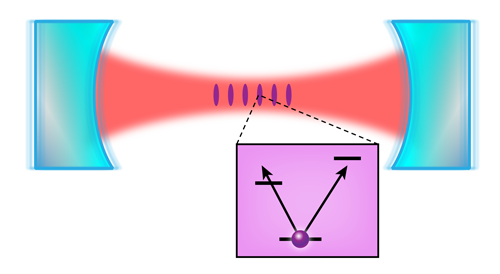
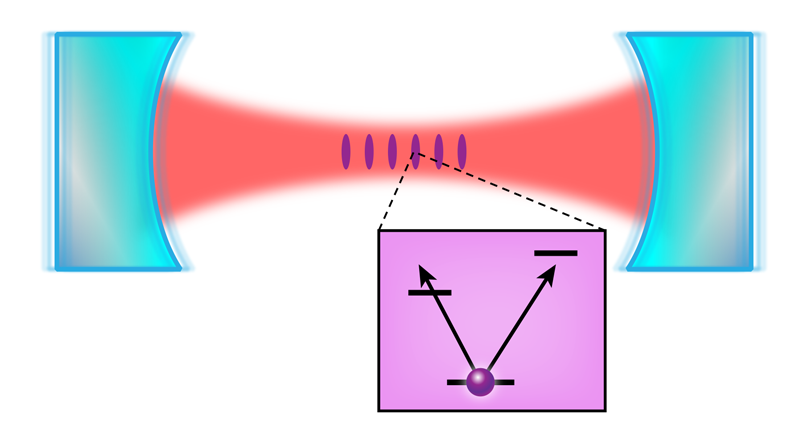
Inducing Transparency with a Magnetic Field
Macroscopic objects vibrate because of their thermal energy, but we do not perceive these vibrations in daily life. However, thermal motion of optical-cavity mirrors limits the frequency stability of state-of-the-art lasers that are used in optical atomic clocks and in searches for new fundamental physical effects. James Thompson from the University of Colorado, Boulder, and colleagues [1] now demonstrate a method to render laser light insensitive to mirror vibrations. They accomplish this by inserting an atomic vapor between the mirrors of an optical cavity and using an effect that is analogous to the phenomenon of electromagnetically induced transparency (EIT). Unlike conventional EIT, the effect relies on a magnetic field rather than a laser to modify the optical properties of an atomic medium, so the researchers term the phenomenon magnetically induced transparency (MIT). Like its electromagnetic counterpart, MIT could also be employed to slow light and store light pulses in an atomic ensemble.
Electromagnetically induced transparency is a quantum optical effect in which light at one frequency from a “control laser” renders a medium transparent to light from a “probe laser” at a second frequency. The transparency, or strong drop in probe-light absorption, also leads to a strong change in the index of refraction of the medium, causing light pulses to travel slowly in the medium [2, 3]. In addition to transparency and slowing of light, EIT can enhance a material’s otherwise small nonlinear optical response, leading to applications in frequency conversion and information processing [4, 5].
In 1998, Mikhail Lukin and colleagues [6] proposed a new application of EIT based on enclosing an atomic medium between two mirrors to form an optical cavity. They predicted that EIT would result in a new optical resonance in the cavity, with a reduced linewidth compared to the empty-cavity linewidth. Just as a tuning fork aids in the adjustment of a musical instrument’s pitch, an optical cavity often serves as a frequency reference to help stabilize the frequency of a laser. By significantly narrowing the cavity resonance, cavity EIT would provide a more precise reference frequency for laser stabilization.
The underlying reason for the reduced linewidth stems from the fact that in EIT, the medium temporarily absorbs most of the probe light into a long-lived atomic excited state, which protects the light from being lost as it normally would through scattering by a shorter-lived excited state. This effect only occurs for light in a narrow range of frequencies that is typically narrower than the width of the cavity resonance in an empty optical cavity. The transfer of light into a long-lived atomic excited state that occurs in EIT has also led to work using EIT to transfer light to highly excited atomic states, called Rydberg states, that induce extremely strong optical nonlinearities [7–9].
In its original form, EIT relies on the additional control laser to modify the optical properties of the medium. The transparency occurs when the difference in frequency between the control laser and the probe laser matches a specific value that depends on the atomic medium. Therefore, conventional EIT can be used to stabilize the frequency difference of two lasers [10]. However, a stable frequency difference is not sufficient for applications requiring absolute frequency stability, such as atomic clocks. The phenomenon of MIT that Thompson and colleagues now introduce gives access to the essential features of EIT, but it only requires a static magnetic field rather than an additional laser to modify the properties of the medium. MIT can thus be used to stabilize a single laser (the probe laser) to an absolute frequency defined by the medium, rather than only stabilizing the laser relative to another laser. As in conventional cavity EIT, in MIT a narrow optical resonance appears in the cavity’s optical transmission spectrum. And similarly to EIT, this resonance arises because of a strongly coupled state of light and matter that can have a larger matter component than optical component. The larger matter component makes the frequency of the resonance largely insensitive to thermal vibrations of the cavity mirrors.
To allow a magnetic field to induce a narrow resonance, Thompson and co-workers employ three energy levels of the strontium-88 atom in a “V” configuration: two long-lived excited states and one ground state (Fig. 1). The excited states have the same energy in the absence of a magnetic field, but in an applied magnetic field, their energy is split by a small amount through the Zeeman effect. Because of the near-degeneracy of the two excited states, a single laser can make the atom transition to either excited state. At zero magnetic field, the three-level system has a so-called dark state, which consists of a coherent superposition of the two excited states and is unresponsive to the probe light. While this dark state has the desired properties of possessing a precise resonant frequency and being insensitive to mirror vibrations, the fact that it doesn’t respond to probe light makes it impossible to access. However, the Zeeman splitting from an applied magnetic field modifies the dark state slightly and allows it to respond to the probe light. The application of a magnetic field therefore causes a new narrow resonance to appear in the cavity’s transmission spectrum. At sufficiently small values of the applied field, the desired characteristics of the dark state remain intact, providing a narrow feature that is largely decoupled from the thermal vibrations of the cavity mirrors.
This narrow feature can serve as an absolute reference in the frequency domain. The key properties of narrow linewidth and insensitivity to thermal mirror vibrations inherited from EIT essentially remove the optical cavity from the problem. However, a beneficial feature of the cavity remains, namely enhanced atom-light coupling, because light bounces back and forth between the cavity mirrors many times. This enhanced coupling is particularly helpful when accessing narrow optical transitions, which can be otherwise difficult to observe (because of Doppler shifts from the motion of the atoms, for example). As Thompson and colleagues point out, one limitation of their scheme is that the signal from the narrow resonance becomes weaker the more one decouples it from the cavity, so one must choose an optimal operating point. It will be interesting to see future work building on this idea of inducing optical transparency magnetically, for example, in photon storage and in the stabilization of the frequency of narrow-linewidth lasers for high-precision measurements.
This research is published in Physical Review Letters.
References
- M. N. Winchester, M. A. Norcia, J. R. K. Cline, and J. K. Thompson, “Magnetically-Induced Optical Transparency on a Forbidden Transition in Strontium for Cavity-Enhanced Spectroscopy,” Phys. Rev. Lett. 118, 263601 (2017).
- K.-J. Boller, A. Imamoğlu, and S. E. Harris, “Observation of Electromagnetically Induced Transparency,” Phys. Rev. Lett. 66, 2593 (1991).
- S. E. Harris, “Electromagnetically Induced Transparency,” Phys. Today 50, No. 7, 36 (1997).
- M. Fleischhauer, A. Imamoğlu, and J. P. Marangos, “Electromagnetically Induced Transparency: Optics in Coherent Media,” Rev. Mod. Phys. 77, 633 (2005).
- D. E. Chang, V. Vuletić, and M. D. Lukin, “Quantum Nonlinear Optics—Photon by Photon,” Nat. Photon. 8, 685 (2014).
- M. D. Lukin, M. Fleischhauer, M. O. Scully, and V. L. Velichansky, “Intracavity Electromagnetically Induced Transparency,” Opt. Lett. 23, 295 (1998).
- V. Parigi, E. Bimbard, J. Stanojevic, A. J. Hilliard, F. Nogrette, R. Tualle-Brouri, A. Ourjoumtsev, and P. Grangier, “Observation and Measurement of Interaction-Induced Dispersive Optical Nonlinearities in an Ensemble of Cold Rydberg Atoms,” Phys. Rev. Lett. 109, 233602 (2012).
- J. Ningyuan, A. Georgakopoulos, A. Ryou, N. Schine, A. Sommer, and J. Simon, “Observation and Characterization of Cavity Rydberg Polaritons,” Phys. Rev. A 93, 041802 (2016).
- J. Ningyuan, N. Schine, A. Georgakopoulos, A. Ryou, A. Sommer, and J. Simon, “A Strongly Interacting Polaritonic Quantum Dot,” arXiv:1705.07475.
- S. C. Bell, D. M. Heywood, J. D. White, J. D. Close, and R. E. Scholten, “Laser Frequency Offset Locking Using Electromagnetically Induced Transparency,” Appl. Phys. Lett. 90, 171120 (2007).