Active-Matter Thermodynamics Under Pressure
How does the volume of a gas respond to rising pressure? How much energy can a material store or release upon a change in temperature? Three centuries ago these questions were at the root of the industrial revolution and of the burgeoning field of thermodynamics, which sought to describe liquids, gases, and solids at thermal equilibrium in terms of a few macroscopic quantities known as state variables. Today researchers are asking the same questions about out-of-equilibrium systems known as active matter—collections of particles that propel themselves by extracting energy from their environment. Active matter can be made from living things like cells or from objects such as colloidal particles, liquid crystals, gels, or grains [1, 2], and it can in many ways resemble liquids and gases. But can active matter be described by state variables? Olivier Dauchot of ESPCI Paris and his colleagues measured the mechanical pressure of a “liquid” of self-propelled disks and found that, at least for this representative active-matter system, mechanical pressure can’t be used as a state variable because it is ill defined [3].
Perhaps the most familiar result from thermodynamics is the equation of state of an ideal gas at thermal equilibrium. This simple equation, P=nkBT, relates the mechanical pressure P on the walls confining the gas to its number density n and temperature T ( kB is the Boltzmann constant). It therefore relates the bulk properties of the gas to a quantity measured at its surface, the mechanical pressure. Notably, the mechanical pressure can be defined independently of the shape or properties of the container. It is in this sense that mechanical pressure is a well-defined state variable.
Whether the concept of a state variable can be extended to nonequilibrium systems is an open question [4]. Theorists have made significant progress addressing this question for active matter [5–8]. In particular, in 2015, theorists considered the specific case of a liquid made of particles that propel themselves along a substrate, and they determined that—apart from situations that would be difficult to realize experimentally [6]—the mechanical pressure of this system is not a state variable [7].
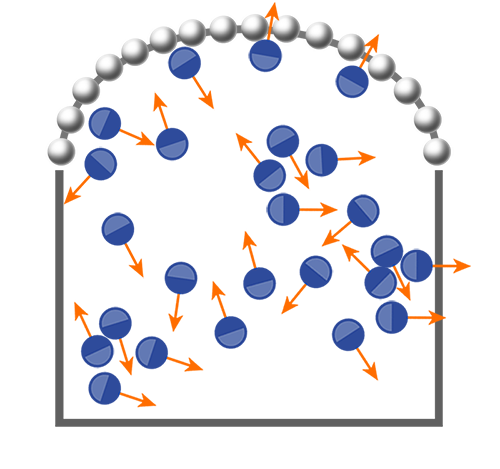
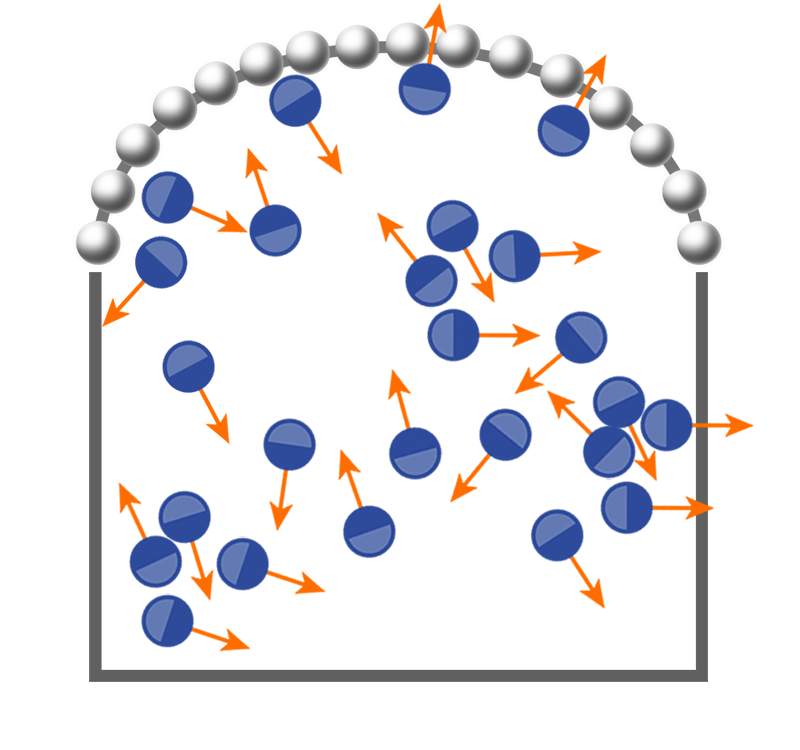
Dauchot and colleagues have now experimentally confirmed this theoretical result [3]. Their setup, which builds on one they devised in 2010, allows them to measure the mechanical pressure of several hundred 5-mm-wide metal disks that skate along the bottom of a shallow box vibrating from below. They perform this measurement on disks that are either perfectly isotropic or that have two “legs” fashioned out of different materials and are therefore polar (Fig. 1). When vibrated, the isotropic disks diffuse “passively,” similarly to Brownian particles in a liquid at thermal equilibrium. By contrast, the two-legged disks are “active”: each disk propels itself along its polar axis, remembering its initial orientation and reorienting only over long time scales. Despite their different dynamics, both systems qualitatively resemble homogeneous liquids.
Dauchot’s team cleverly measured the minute pressure that the disks exert on the confining walls with a force-sensing tool that you might find in your bathroom tub: the beaded chain dangling from a drain stopper. When this chain serves as one wall for the vibrating disks, it will, on average, bulge outwards in an arc (Fig. 1), indicating a uniform pressure inside the box. The team assumed the chain is analogous to an elastic polymer at thermal equilibrium and used Laplace’s law to determine the pressure exerted on the chain from its tension.
The team focused first on the isotropic (passive) disks. They used one chain to measure the pressure from the disks as a function of disk density. They then repeated the measurement with a chain made from a larger number of beads of smaller size than in the first chain, finding the same relationship between pressure and density. Remarkably, this “equation of state” for the shaken isotropic disks, a nonequilibrium system, is the same as that found for hard disks at thermal equilibrium. By contrast, when they conducted the same experiment with the two-legged (active) disks, they found that the pressure-density relationship depended on which chain sensor they used. Simply put, pressure is not a state variable for the system of self-propelled disks.
The team went further by using a flexible chain to measure the differential pressure between two compartments containing two-legged disks with different packing fractions. The researchers found not only that the pressure difference across the chain was not uniform, but also that it was not equal to the expected difference in pressure between the two systems in isolation. These findings, which are reminiscent of instabilities observed in numerical simulations of active liquids [9], further establish that mechanical pressure is not a state variable of the active disks.
Those familiar with the active-matter literature may be baffled by the results from Dauchot’s team. In 2015, another French group combined experiments on active colloids with simulations, demonstrating that an equation of state relating pressure to bulk density was in fact possible for these systems [8]. The apparent discrepancy with the new experiment can be resolved by carefully defining pressure. Dauchot and colleagues probed the average force at the surface of the confining walls. In the 2015 experiment, the researchers instead determined the normal stress in the bulk of the colloidal liquid. However, the surface pressure and the bulk stress are only identical at thermal equilibrium, a condition that doesn’t apply to either of the experiments [7]. Put differently, it is possible to define an equation of state for active matter with pressure as a state variable, but the “pressure” in this case does not correspond to an average mechanical force acting on the walls of the container, as it does for an ideal gas.
Is defining the equation of state for active matter merely of academic interest? For now, we don’t know. It could become influential if researchers are able to produce practically useful active materials or to extend the elegant experiments and theories that describe self-propelled disks and colloids to nature’s most abundant type of active matter: cells. Biological systems are typically associated with different symmetries and conservation laws than granular and colloidal systems. Defining an equation of state for cell tissue would, without a doubt, be a breakthrough. But for the theoretical, experimental, and simulation tools available today, such a description is still out of reach.
This research is published in Physical Review Letters.
Correction (17 July 2017): The article was updated to include the reference to the paper by X. Yang et al. in Ref. [5].
References
- M. C. Marchetti et al., “Hydrodynamics of Soft Active Matter,” Rev. Mod. Phys. 85, 1143 (2013).
- A. Zöttl and H. Stark, “Emergent Behavior in Active Colloids,” J. Phys. Condens. Matter 28, 253001 (2016).
- G. Junot, G. Briand, R. Ledesma-Alonso, and O. Dauchot, “Active versus Passive Hard Disks Against a Membrane: Mechanical Pressure and Instability,” Phys. Rev. Lett. 119, 028002 (2017).
- L. F. Cugliandolo, “The Effective Temperature,” J. Phys. A 44, 483001 (2011); L. J. Daniels, T. K. Haxton, N. Xu, A. J. Liu, and D. J. Durian, “Temperature-Pressure Scaling for Air-Fluidized Grains near Jamming,” Phys. Rev. Lett. 108, 138001 (2012); E. Bertin, O. Dauchot, and M. Droz, “Definition and Relevance of Nonequilibrium Intensive Thermodynamic Parameters,” 96, 120601 (2006); H. A. Makse and J. Kurchan, “Testing the Thermodynamic Approach to Granular Matter with a Numerical Model of a Decisive Experiment,” Nature 415, 614 (2002).
- S. C. Takatori, W. Yan, and J. F. Brady, “Swim Pressure: Stress Generation in Active Matter,” Phys. Rev. Lett. 113, 028103 (2014); S. C. Takatori and J. F. Brady, “Towards a Thermodynamics of Active Matter,” Phys. Rev. E 91, 032117 (2015); X. Yang, M. L. Manning, and M. C. Marchetti, “Aggregation and Segregation of Confined Active Particles,” Soft Matter 10, 6477 (2014).
- A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates, and J. Tailleur, “Pressure and Phase Equilibria in Interacting Active Brownian Spheres,” Phys. Rev. Lett. 114, 198301 (2015).
- A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar, and J. Tailleur, “Pressure is Not a State Function for Generic Active Fluids,” Nat. Phys. 11, 673 (2015).
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier, and C. Cottin-Bizonne, “Nonequilibrium Equation of State in Suspensions of Active Colloids,” Phys. Rev. X 5, 011004 (2015).
- N. Nikola, A. P. Solon, Y. Kafri, M. Kardar, J. Tailleur, and R. Voituriez, “Active Particles with Soft and Curved Walls: Equation of State, Ratchets, and Instabilities,” Phys. Rev. Lett. 117, 098001 (2016).