Spinning Black Holes May Grow Hair
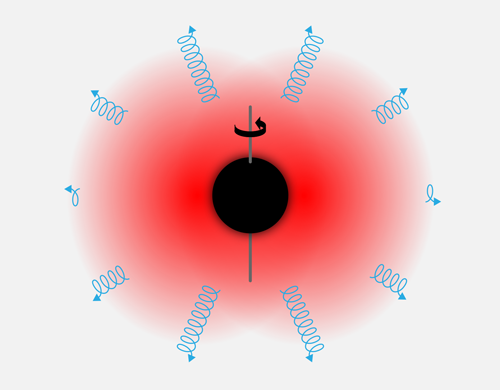
New simulations of the dynamics of spinning black holes by William East from the Perimeter Institute for Theoretical Physics, Canada, and Frans Pretorius from Princeton University, New Jersey [1], have shed light on an intriguing possibility. If there exists in nature a bosonic particle with an exceptionally small mass ( <10−10eV∕c2), then a black hole may spontaneously grow “long hair,” in the form of highly amplified excitations of the field that are trapped in the vicinity of the black hole (Fig. 1). The finding suggests that black holes may grow hair that is long-lived and extends well beyond the black hole event horizon. This conclusion poses a challenge to the cherished “no-hair” paradigm. It also raises the possibility that black holes with hair, if they exist, may one day be detected via their gravitational-wave signatures.
The new work is rooted in two influential ideas about black holes from the early 1970s, as popularized by John Wheeler and Roger Penrose. “A black hole has no hair,” claimed Wheeler in 1971. Howsoever it comes into being, a black hole is expected to quickly settle into a stationary state that is described by just three quantities: mass, angular momentum, and charge. All other degrees of freedom—for which hair is a metaphor—are quickly radiated away or absorbed. In the classical theory, the black hole retains no detailed memory of that which it has swallowed. Remarkably, the no-hair paradigm gained experimental support last year, through the first gravitational-wave event detected by the Laser Interferometer Gravitational-Wave Observatory (LIGO). The “chirp” signal seen at LIGO appears to confirm that when two black holes coalesce, they produce a new black hole that, after a rapid relaxation, differs from its progenitors only through its mass and spin (see 31 May 2016 Viewpoint).
Penrose’s insight was that, in principle, the mass and spin in a black hole can be unleashed to drive powerful processes, such as jets and quasars. In 1971, Penrose described a thought experiment in which a black hole transfers some of its energy and angular momentum into a scattered particle. In similar fashion, an electromagnetic wave reflecting off a spinning black hole may be boosted by extracting energy and angular momentum from the black hole, in a process called black hole superradiance.
In 1972, researchers suggested [2] that a runaway process called a black hole bomb would be triggered if superradiance were repeatedly reflected back onto the black hole. Such a process may arise spontaneously if there exists in nature a field of bosonic particles with a very light mass, because certain modes of the field will become trapped within the black hole’s gravitational potential well [3]. It turns out that long-wavelength, co-spinning modes of the field can grow exponentially in amplitude, via superradiance, until the field becomes so strong that nonlinear effects—such as the extra curvature of spacetime—start to play a significant role [4]. For this to happen on a reasonable time scale of a few years or less, the mass of the bosonic field must be so very small that the Compton wavelength of the field, which is inversely proportional to the particles’ mass, is comparable to the horizon radius of the black hole itself [5]. For example, a solar-mass black hole would be sensitive to a particle approximately 1017 times lighter than the electron.
For now, all this remains hypothetical, but researchers have ways to test the idea. Over the last decade, it has been argued that spinning black holes may act as sensitive probes of new physics [6]. Speculatively, astronomers could seek to infer the existence of ultralight bosons—such as a QCD axion, the string axiverse, or a “fuzzy” dark matter particle—by searching the heavens for the signature of a black hole bomb [7]. But what exactly should one look for?
The new work by East and Pretorius addresses this central question. The researchers numerically simulated the growth of a black hole bomb in the nonlinear regime to determine its final fate. It had been suggested that the black hole would expel the field in an explosive outflow of mass and energy called a bosenova [8] and then begin a new cycle of growth. East and Pretorius’ simulations showed, by contrast, that the black hole can settle into a quasistable equilibrium with the field. In the specific case of a vector boson field with a Compton wavelength comparable to the event-horizon radius, they showed that up to 9% of the black hole’s mass can be transferred to boost the gravitationally bound dipolar modes of the surrounding bosonic field. In other words, a spinning black hole can grow “long hair”; hair that is both long-lived (at least in comparison to the light-crossing time of the black hole) and that extends quite far outside the event horizon.
A key lesson from East and Pretorius’ work is that a black hole bomb may not be explosive after all. Hair growth seems to occur in a remarkably smooth manner, and the runaway phase comes to an end without any calamity. The final outcome is a black hole embedded in a massive bosonic field that is orbiting around the black hole at precisely the angular frequency of the black hole horizon. This sort of system is conjectured to be part of the Herdeiro-Radu family of black holes with hair [9].
How might a black hole with hair be detected? A black hole with hair is expected to radiate gravitational waves at a rather monotonous frequency as it spins [6]. Such a steady hum coming from multiple black holes could produce both a stochastic background and resolvable events that might be detected by LIGO and the (future) spaced-based mission LISA. Forthcoming gravitational-wave data may put strong constraints on the existence of ultralight fields with masses in the ranges ∼10−11– 10−14eV∕c2 (LIGO) and ∼10−15– 10−19eV∕c2 (LISA) [10]. It’s an intriguing prospect—using gravitational-wave detectors to look for fundamental bosons—especially in an era in which the cost of the next-generation particle accelerator may prove prohibitive.
This research is published in Physical Review Letters.
References
- W. E. East and F. Pretorius, “Superradiant Instability and Backreaction of Massive Vector Fields around Kerr Black Holes,” Phys. Rev. Lett. 119, 041101 (2017).
- W. H. Press and S. A. Teukolsky, “Floating Orbits, Superradiant Scattering and the Black-hole Bomb,” Nature 238, 211 (1972).
- T. Damour, N. Deruelle, and R. Ruffini, “On Quantum Resonances in Stationary Geometries,” Lett. Nuovo Cimento 15, 257 (1976).
- H. Witek, V. Cardoso, A. Ishibashi, and U. Sperhake, “Superradiant Instabilities in Astrophysical Systems,” Phys. Rev. D 87, 043513 (2013).
- S. R. Dolan, “Instability of the Massive Klein-Gordon Field on the Kerr Spacetime,” Phys. Rev. D 76, 084001 (2007).
- A. Arvanitaki, S. Dimopoulos, S. Dubovsky, N. Kaloper, and J. March-Russell, “String Axiverse,” Phys. Rev. D 81, 123530 (2010).
- P. Pani, V. Cardoso, L. Gualtieri, E. Berti, and A. Ishibashi, “Black-Hole Bombs and Photon-Mass Bounds,” Phys. Rev. Lett. 109, 131102 (2012).
- H. Yoshino and H. Kodama, “Bosenova Collapse of Axion Cloud around a Rotating Black Hole,” Prog. Theor. Phys. 128, 153 (2012).
- C. Herdeiro, E. Radu, and H. Rúnarsson, “Kerr Black Holes with Proca Hair,” Class. Quantum Grav. 33, 154001 (2016).
- R. Brito, S. Ghosh, E. Barausse, E. Berti, V. Cardoso, I. Dvorkin, A. Klein, and P. Pani, “Gravitational Wave Searches for Ultralight Bosons with LIGO and LISA,” arXiv:1706.06311.