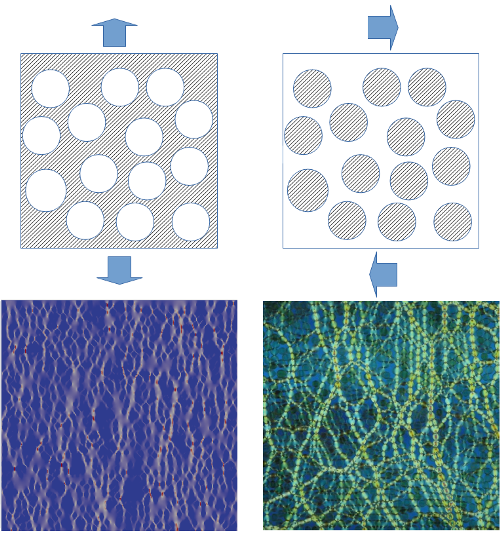
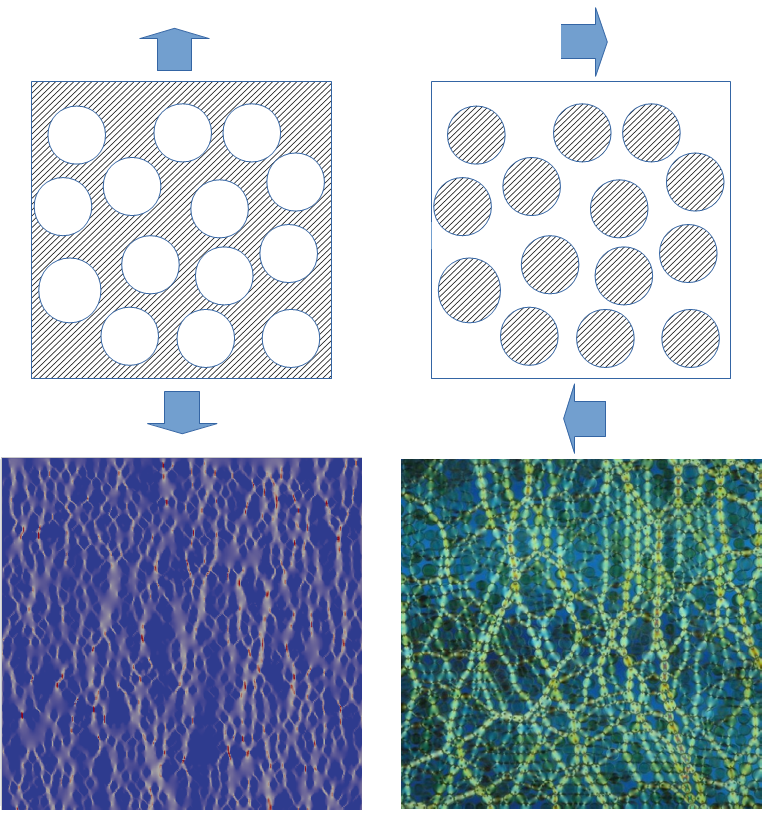
Porous Materials Exhibit Granular-Like Stress Chains
Porous materials are ubiquitous—from ceramics to lightweight concrete to human bone. At first glance, these hole-filled materials are the exact opposite of granular materials, such as a bed of sand. In porous materials we have unconnected voids embedded in a continuous, cohesive solid, whereas in granular materials we have empty space filled with distinct solid particles that interact through repulsive and frictional contact forces. Nevertheless, Hadrien Laubie and co-workers from the Massachusetts Institute of Technology, Cambridge [1], have demonstrated surprising analogies between disordered porous materials and “jammed” packings of grains [2, 3]. Even though the distribution of matter is very different in the two types of materials, the team’s simulations show that the mechanisms that control the strength of both kinds of material turn out to be very much the same. In both cases, the force from an externally applied load is transmitted by highly heterogeneous stress chains, which—in materials on the brink of failure—may span the entire sample. The heterogeneity of stress transmission increases with the level of disorder in the pore arrangement, and the authors demonstrate that this leads to a loss of material strength, an observation that might be true for many other heterogeneous systems as well.
Despite their low density, porous materials like bone can be very strong. Modeling the effective mechanical behavior of a solid with pores is a textbook mechanics problem. As with other heterogeneous materials, the standard approach is called homogenization: Scientists aim at discarding microstructural detail and instead describe the system in terms of simple statistical parameters. In the case of a porous material, the relevant parameter is the pore volume fraction. In such a homogenized approach, the stresses and strains in between the pores are assumed to be essentially uniform. However, Laubie et al. show that this is far from correct: they find that greater disorder in the arrangement of pores can increase the likelihood of material failure, implying that microstructural details are indeed important.
In their lattice element simulations, Laubie and colleagues explore the spatial and statistical distribution of stresses that develop in two-dimensional porous materials with different degrees of disorder as the materials are subjected to a tensile load. They model the solid in between the pores as a regular network of springs, allowing them to study the internal stress pattern through the spatial distribution of spring forces. The researchers can also model material failure by assuming that an individual spring will break if the force on it reaches a critical value.
The researchers started with pores in an ordered lattice and then increased the disorder by introducing random displacements of the pores. For a low-disorder system, the observed stress pattern in the simulated pore material is fairly homogeneous—as expected from standard approaches. However, with an increasing degree of disorder, the team observed the development of pronounced stress transmission chains. These lines of concentrated stress resemble the force chains found in granular materials where shear forces have induced a “jamming transition,” in which grains stop sliding and instead lock into a solid, compact arrangement (Fig. 1). The analogy between grains and pores goes beyond mere visible likeness, as the probability distribution of local stresses in both types of materials develops a characteristic asymmetric shape with an exponential tail.
The researchers also analyzed the failure behavior of porous materials, using methods that some of the authors have developed previously for assessing the stability of sand piles and the initiation of sand avalanches [4, 5]. The authors identify, for a given applied stress, those critical locations where the local stress exceeds the system failure stress, which is proportional to the critical spring force. They then investigate the spatial extension of the surrounding over-loaded regions. Near the failure stress, the size of the largest over-loaded region increases very rapidly according to a power law—an observation that agrees with the findings on granular materials close to the initiation of a granular avalanche [4, 5].
Having established that a disordered porous material can resemble a granular system, the team investigated the effect of increasing disorder further. They found that as disorder goes up, the strength of a porous material decreases proportionally and may even reach zero if the porosity is high enough. The stress pattern in such highly disordered porous solids is characterized by extended stress correlations in the form of stress chains, and failure occurs by the percolation of over-loaded regions across the sample.
The near-exact match between these findings in porous solids and in granular materials at the jamming transition threshold raises an intriguing question: Is it possible that the observed analogies between porous and granular materials point towards a larger degree of universality? In other words, can we identify general principles which govern the behavior of all materials that possess a sufficient degree of disorder as they approach material failure? Knowledge of such principles could be helpful for materials and process design in view of improving strength through controlling disorder. It might also help in structural safety assessment by identifying possible disorder-dependent failure precursors.
Before this question can be resolved there are still important practical issues to address. Most obviously, the work of Laubie et al. is restricted to highly idealized, two-dimensional systems where porosity is represented by holes in a planar solid. Real porous materials are three dimensional, so it will be necessary to verify if the current results can be reproduced in three-dimensional simulations as well as in experiments. A second important issue concerns the size-dependency of strength. It is well known for disordered materials such as brittle foams [6] that the strength may decrease with increasing sample size because of the greater likelihood of encountering a weak region in a larger volume [7]. Do such size effects exist in disordered porous materials, and if yes, how do they fit into the picture of failure developed in this new disorder-based model? Systematic large-scale simulations can sort out these issues, and one may look forward to the further insights they will provide into the failure of disordered materials.
This research is published in Physical Review Letters.
References
- H. Laubie, F. Radjai, R. Pellenq, and F.-J. Ulm, “Stress Transmission and Failure in Disordered Porous Media,” Phys. Rev. Lett. 119, 075501 (2017).
- R. P. Behringer, D. Bi, B. Chakraborty, A. Clark, J. Dijksman, J. Ren, and J. Zhang, “Statistical Properties of Granular Materials Near Jamming,” J. Stat. Mech. 2014, P06004 (2014).
- D. Bi, J. Zhang, B. Chakraborty, and R. P. Behringer, “Jamming by Shear,” Nature 480, 355 (2011).
- L. Staron, F. Radjai, and J.-P. Vilotte, “Multi-Scale Analysis of the Stress State in a Granular Slope in Transition to Failure,” Euro. Phys. J. E 18, 311 (2005).
- L. Staron, J.-P. Vilotte, and F. Radjai, “Preavalanche Instabilities in a Granular Pile,” Phys. Rev. Lett. 89, 204302 (2002).
- R. J. Mora and A. M. Waas, “Strength Scaling of Brittle Graphitic Foam,” Proc. R. Soc. London A 458, 1695 (2002).
- A. Shekhawat, S. Zapperi, and J. P. Sethna, “From Damage Percolation to Crack Nucleation Through Finite Size Criticality,” Phys. Rev. Lett. 110, 185505 (2013).