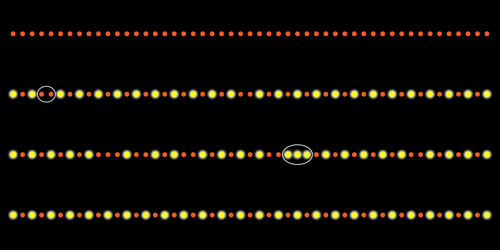
Cold Atoms Bear a Quantum Scar
Researchers still have some way to go before they can assemble enough quantum bits (qubits) to make a practical, large-scale quantum computer. But already the best prototypes, made up of several tens of qubits, are opening our eyes to new behavior in the quantum realm. Last year, a team from Harvard University and the Massachusetts Institute of Technology (MIT) unveiled a quantum “simulator” made up of a row of 51 interacting atoms [1]. Exciting the individual atoms in various patterns (Fig. 1), they discovered something unexpected: atoms in certain patterns took at least 10 times longer to relax towards thermal equilibrium than atoms in other patterns. Four groups of theorists have tried to make sense of this observation [2–6], in all cases attributing the slow thermalization to a never-before-seen effect called quantum many-body scarring. Because scarring protects a quantum system from the scrambling of information caused by thermalization, the effect may prove useful for quantum computing.
The notion of a quantum scar was introduced in the early 1980s in a theoretical paper by physicist Eric Heller [7]. Researchers had long known that a classical chaotic system can still display periodic behavior. For example, a frictionless billiard ball set to bounce around a stadium-shaped table will typically follow a nonrepeating path, undergoing motion that is called ergodic because it explores all points on the table. But for certain initial angles, the ball retraces its path after a certain number of bounces. Such periodic trajectories are unstable to small shifts that send the ball onto a nonrepeating path. Heller considered what would happen if the classical billiard problem were translated into the “particle in a box” problem of quantum mechanics, where the ball is replaced with a quantum particle whose energy is quantized [7]. He found that certain quantum states bear an imprint, or “scar,” from the classical periodic orbits. A particle in one of these scarred states is much more likely to be found near an unstable periodic path.
So far, physicists haven’t succeeded in generalizing Heller’s description of a single quantum particle to the much more complicated case of many interacting particles. However, the Harvard-MIT experiment and the theoretical papers it has inspired suggest that many-body quantum scarring may have been observed [1–6]. In the experiments, the 51 atoms were spaced a few micrometers apart in a linear array, and each atom could be prepared in either its ground state or a highly excited “Rydberg” state (Fig. 1). The researchers then turned on interactions between the atoms, allowing the exchange of energy, and they tracked the evolving distribution of excited atoms by detecting the fluorescence of individual atoms. The researchers expected that after some characteristic time, the atom chain would thermalize, redistributing the initial energy among the atoms as the chain passed through many possible quantum states.
For most cases, thermalization proceeded as expected. But when the team initialized the simulator with a pattern in which every other atom was in an excited state, they found that thermalization took at least 10 times longer. This slow-to-thermalize case also exhibited long-lived oscillations—sloshing back and forth between two patterns where every other atom is excited. In the same way that the bouncing ball with a periodic path doesn’t visit all points on the table, the oscillating array of atoms in the chain didn’t sample all of its possible quantum states. The system’s ergodicity was therefore broken.
Earlier numerical simulations of Rydberg atom chains had, in fact, given similar results [8], with some initial patterns resulting in slow-to-thermalize, nonergodic behavior [9]. An explanation for this behavior, however, has remained a challenge for theory. Nonergodic behavior is usually found in systems that are subject to a large number of conservation laws, which restricts how the system can evolve. But the atom chains do not appear to be highly constrained—the only quantity known to be conserved in the experiment and the numerical simulations is the energy. So what was going on?
The four theoretical groups addressing this question have all done so by studying essentially the same so-called PXP model. This model assumes the atoms can be in one of two states: the ground state or an excited Rydberg state. The model also explicitly excludes two excited atoms from sitting next to each other, as they strongly repel. Christopher Turner of the University of Leeds, UK, and collaborators, who were the first to connect slow thermalization and quantum many-body scars [2], use state-of-the-art numerical tools to find the spectrum of allowed quantum states for the PXP model [2, 3]. Embedded in this spectrum, they identify a small number of states—the scarred states—with three special properties: they are almost equally spaced in energy, they give nonthermal expectation values for various observables, and they are only weakly entangled. Turner and colleagues show that the configuration in which every other atom is excited projects strongly onto these scarred states. Because of the special properties of the scarred states, this configuration then exhibits oscillatory dynamics and slow thermalization.
The three other groups study different aspects of the PXP model in various ways. Wen Wei Ho and coauthors from Harvard represent the initial configuration of atoms as a superposition of a restricted set of states; by design, each state in this superposition has the low entanglement expected for scarred states [4]. They then compute how the initial pattern of excited atoms evolves in time, all the while assuming the chain can be represented in terms of the restricted set of states. In doing so, they find that the atoms can periodically sweep through certain patterns. While their assumption may not be mathematically rigorous, they do suggest that their approach might be used to generalize single-particle quantum scars to the many-body case.
A different perspective is provided by Vedika Khemani, also of Harvard, and co-workers [5]. They provide numerical evidence that, with certain minor modifications, the PXP model has the property of being “integrable.” A collection of particles is said to be integrable if it has the rare attribute of being governed by more conservation laws as the particle number increases. Khemani and colleagues show that deforming the model towards this “integrable point” enhances the long-lived periodic oscillations, leading them to suggest that scarred states are connected to integrability.
Finally, the most recent contribution comes from Cheng-Ju Lin and Olexei Motrunich from the California Institute of Technology in Pasadena. They obtain scarred states by exciting two states found in the middle of the chain’s many-body spectrum [6]. In their picture, the experimental oscillations are associated with transitions between these excited states, and the frequency of the oscillations is governed by the energy of the excitations.
These papers clearly show enthusiasm for quantum many-body scarring, but much about the phenomenon remain unclear. Perhaps most glaringly, we don’t have a governing principle for how and when quantum many-body scars will appear. Progress on this front might be made by trying to unite the approaches and interpretations of Refs. [2–6], and to this end, there is a lot to explore. Can the approach of Ho and collaborators [4] be made mathematically rigorous? This would solidify the connection between the special states and quantum scarring. Are quantum scars connected to integrability, as put forth by Khemani and colleagues [5]? If so, then quantum scarring should fade away in the PXP model with larger numbers of atoms. Is the constraint of forbidding two neighboring excited atoms an important condition for scarring [2–6]? The answer is unclear, given that other models with similar restrictions do not show scarring [10]. However, constraints do play a role in the nonthermal behavior predicted for certain other quantum systems [11]—might this behavior also be interpreted in terms of quantum many-body scars?
Quantum scarring may seem like an abstract mathematical topic. But it is of practical interest for the field of quantum computing. If a many-body system is prepared in a scarred state, it is effectively shielded from thermalization for long times, which would make a scarred state attractive for storing quantum information. This exciting possibility motivates further research aimed at finding the right conditions for forming a quantum scar.
This research is published in Nature Physics, Physical Review B, and posted on the arXiv.
References
- H. Bernien et al., “Probing many-body dynamics on a 51-atom quantum simulator,” Nature 551, 579 (2017).
- C. J. Turner, A. A. Michailidis, D. A. Abanin, M. Serbyn, and Z. Papić, “Weak ergodicity breaking from quantum many-body scars,” Nat. Phys. 14, 745 (2018).
- C. J. Turner, A. A. Michailidis, D. A. Abanin, M. Serbyn, and Z. Papić, “Quantum scarred eigenstates in a Rydberg atom chain: Entanglement, breakdown of thermalization, and stability to perturbations,” Phys. Rev. B 98, 155134 (2018).
- W. W. Ho, S. Choi, H. Pichler, and M. D. Lukin, “Periodic orbits, entanglement and quantum many-body scars in constrained models: Matrix product state approach,” arXiv:1807.01815.
- V. Khemani, C. R. Laumann, and A. Chandran, “Signatures of integrability in the dynamics of Rydberg-blockaded chains,” arXiv:1807.02108.
- C.-J. Lin and A. Motrunich, “Exact strong-ETH violating eigenstates in the Rydberg-blockaded atom chain,” arXiv:1810.00888.
- E. J. Heller, “Bound-state eigenfunctions of classically chaotic hamiltonian systems: Scars of periodic orbits,” Phys. Rev. Lett. 53, 1515 (1984).
- B. Sun and F. Robicheaux, “Numerical study of two-body correlation in a 1D lattice with perfect blockade,” New J. Phys. 10, 045032 (2008).
- C. Ates, J. P. Garrahan, and I. Lesanovsky, “Thermalization of a strongly interacting closed spin system: From coherent many-body dynamics to a Fokker-Planck equation,” Phys. Rev. Lett. 108, 110603 (2012).
- A. Chandran, M. D. Schulz, and F. J. Burnell, “The eigenstate thermalization hypothesis in constrained Hilbert spaces: A case study in non-Abelian anyon chains,” Phys. Rev. B 94, 235122 (2016).
- Z. Lan, M. van Horssen, S. Powell, and J. P. Garrahan, “Quantum slow relaxation and metastability due to dynamical constraints,” Phys. Rev. Lett. 121, 040603 (2018).