The Plot Thickens for a Fourth Neutrino

Joachim Kopp

Viewpoint

The Plot Thickens for a Fourth Neutrino

Theoretical Physics Department, CERN, Geneva, Switzerland
PRISMA Cluster of Excellence, Mainz, Germany

November 26, 2018• Physics 11, 122

Confirming previous controversial results, the MiniBooNE experiment detects a signal that is incompatible with neutrino oscillations involving just the three known flavors of neutrinos.

Figure caption — **Figure 1:** Scheme of the MiniBooNE experiment at Fermilab. A high-intensity beam of accelerated protons is focused onto a target, producing pions that decay predominantly into muons and muon neutrinos. The resulting neutrino beam is characterized by the MiniBooNE detector.

Neutrinos have always been good for surprises. The postulate of their existence by Wolfgang Pauli in 1930 was already revolutionary. Later, physicists learned that neutrinos oscillate, meaning that the three known neutrino “flavors” (electron, muon, and tau) periodically convert into one another as they travel through space—a neutrino born in the muon flavor, for instance, may later be detected as an electron neutrino or tau neutrino. The discovery of neutrino oscillations implied that neutrinos have nonzero mass, which required a modification of the standard model of particle physics. Adding another surprise, the parameters that govern neutrino oscillations turned out to be vastly different from theoretical expectations.

Now, the MiniBooNE experiment at Fermilab in Illinois has reignited excitement about neutrinos on yet another front. Data from the experiment suggest that muon neutrinos convert into electron neutrinos over distances that are too short for conventional neutrino oscillations to occur [1]. This finding is all the more intriguing when considering that an earlier experiment—the Liquid Scintillator Neutrino Detector (LSND) at Los Alamos—already observed a similar signal in the late 1990s [2]. The reason for excitement is that these signals could be beacons of sterile neutrinos, particles that only interact through gravity and aren’t foreseen in the standard model. The existence of sterile neutrinos could lead us to answers to some of the most pressing puzzles in physics—from the nature of dark matter to matter asymmetry in the Universe.

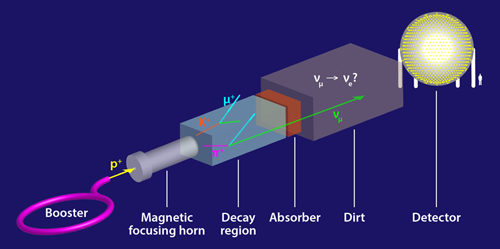
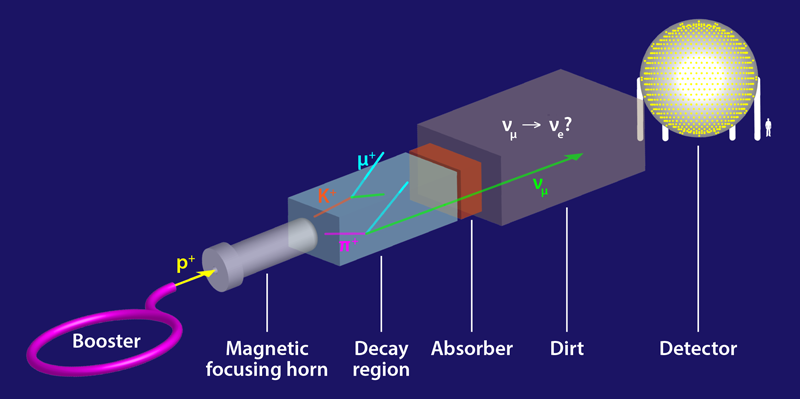
MiniBooNE receives neutrinos that are produced by dumping a high-intensity beam of accelerated protons onto a solid target (Fig. 1). The nuclear debris that emerges from these collisions consists mostly of pions—unstable particles that live less than a microsecond before decaying, predominantly into muons and muon neutrinos. The resulting muon neutrino beam travels about half a kilometer to the MiniBooNE detector, a spherical tank filled with 818 tons of mineral oil [3]. When an incoming neutrino interacts with an atomic nucleus inside the detector, it produces particles that can be used to detect neutrinos and determine their flavor (typically, a muon neutrino produces a high-energy muon, while an electron neutrino produces a high-energy electron). Using this method, MiniBooNE finds significantly more electron-neutrino-like events than expected from neutrino oscillations or known backgrounds.

What could explain this excess? Immediately after the LSND observations, theorists put forward the idea that the electron neutrino excess could be due to a fourth, sterile neutrino. To understand why a sterile neutrino would explain the signal observed by LSND, and now by MiniBooNE, we have to delve deeper into the quantum mechanics of neutrino oscillations. One of the defining properties of neutrinos is that the electron neutrino, muon neutrino, and tau neutrino states (collectively referred to as flavor eigenstates) do not have definite masses. Rather, each flavor eigenstate is a quantum-mechanical superposition of mass eigenstates denoted as $𝜈_{1}$ , $𝜈_{2}$ , and $𝜈_{3}$ . A neutrino produced in radioactive processes such as pion decay is always in one of the flavor eigenstates. As it propagates through space, however, the quantum-mechanical phases of the three mass states evolve at different rates. After a while, the neutrino evolves into a different superposition, that is, a different flavor eigenstate. This is why neutrinos oscillate. The lengths over which oscillations occur are inversely proportional to the mass-squared differences $Δ m_{i j}^{2} = m_{i}^{2} - m_{j}^{2}$ (where $i, j = 1, 2,$ or $3$ label the three mass eigenstates). These lengths have been accurately measured and are incompatible with the MiniBooNE result. However, introducing a sterile neutrino allows for a fourth mass eigenstate $𝜈_{4}$ , and thus for a new oscillation length proportional to the mass-squared difference $Δ m_{41}^{2}$ . By including a fourth neutrino with an appropriate value of $Δ m_{41}^{2}$ , flavor conversions mediated by the new state can occur more quickly than without it. In particular, muon-to-electron neutrino oscillation rates consistent with the MiniBooNE results become possible. Intriguingly, the same $Δ m_{41}^{2}$ value explains both the MiniBooNE and LSND results, even though the two experimental setups were very different.

The sterile neutrino hypothesis has received support beyond the findings from LSND and MiniBooNE. Experiments at nuclear reactors [4] and with large samples of radioactive elements [5] have revealed fewer electron neutrinos than expected. This apparent disappearance of electron neutrinos isn’t compatible with the three-neutrino framework, but it could be explained by introducing a sterile neutrino. The idea is that the electron neutrinos oscillate into the sterile state, which can’t be detected.

Alas, other experiments have made serious dents in the sterile neutrino theory. In particular, the model predicts that not only would electron (anti)neutrinos sometimes disappear into the sterile state, but so would muon neutrinos. However, all searches for such muon neutrino disappearance in the required parameter range have come up empty [6], disfavoring the sterile neutrino hypothesis [7]. Alternatives to sterile neutrinos have been proposed, invoking, for instance, other non-standard-model particles that are much heavier [8]. The decay products of these particles could be misinterpreted as electron neutrinos in the MiniBooNE and LSND experiments, explaining the apparent electron neutrino excess. But a recent theoretical analysis indicated that scenarios of this type have problems too [9].

Could the MiniBooNE neutrino excess be explained by more mundane effects? One hypothesis is that the anomalous signal may not be due to electron neutrinos but to backgrounds that produce similar signatures in the detectors. Possible candidates are neutral pions ( $𝜋^{0}$ ), which can be produced when neutrinos scatter off nuclei. The decay of neutral pions would produce photons that could be mistaken as the high-energy electrons produced by electron neutrinos in the detector. (The MiniBooNE collaboration has carried out dedicated measurements to estimate the $𝜋^{0}$ production rate, concluding that it isn’t likely to explain the observed excess [1]). But to be sure, the researchers will need to conduct a direct experimental characterization of $𝜋^{0}$ contamination in their signal. Explanations based on uncertainties in nuclear-physics estimates of the neutrino interaction cross sections are still under debate, though some of them have been disfavored [10]. Currently, a new generation of experiments, at Fermilab and elsewhere, is underway, which may provide definite answers. And the MiniBooNE detector will be complemented by several liquid-argon detectors, which will be able to characterize the $𝜋^{0}$ background in a much better way. Even if it turns out that the MiniBooNE signal comes from $𝜋^{0}$ contamination, we will have learned important lessons that affect future experiments like the huge upcoming neutrino observatories DUNE and Hyper-Kamiokande.

Where does this leave us? Evidence for anomalous behavior in neutrino oscillations is now coming from multiple experiments that use very different setups and technologies. Since none of the observed anomalies can be convincingly explained with the standard model, it is hard not to get excited. There is a chance that these neutrino oscillations are the much sought-after window into “new physics” that will help us resolve the standard model’s shortcomings. However, none of the standard model extensions proposed so far consistently explain all of the observed anomalies, so it is premature to shout “Eureka!” just yet.

This research is published in Physical Review Letters.

References

A. A. Aguilar-Arevalo et al. (MiniBooNE Collaboration), “Significant excess of electronlike events in the MiniBooNE short-baseline neutrino experiment,” Phys. Rev. Lett. 121, 221801 (2018).
C. Athanassopoulos et al., “Candidate Events in a Search forν ${\bar{𝜈}}_{𝜇} \to {\bar{𝜈}}_{e}$ Oscillations,” Phys. Rev. Lett . 75, 2650 (1995); A. Aguilar et al., “Evidence for neutrino oscillations from the observation of ${\bar{𝜈}}_{e}$ appearance in a ${\bar{𝜈}}_{𝜇}$ beam,” Phys. Rev. D 64, 112007 (2001).
A. A. Aguilar-Arevalo et al., “The MiniBooNE detector,” Nucl. Instrum. Meth. Phys. Res., Sect. A 599, 28 (2009).
G. Mention et al., “Reactor antineutrino anomaly,” Phys. Rev. D 83, 073006 (2011).
M. A. Acero, C. Giunti, and M. Laveder, “Limits on $𝜈_{e}$ and ${\bar{𝜈}}_{e}$ disappearance from gallium and reactor experiments,” Phys. Rev. D 78, 073009 (2008).
G. Cheng et al. (MiniBooNE and SciBooNE Collaborations), “Dual baseline search for muon antineutrino disappearance at $0.1 {eV}^{2} < Δ m^{2} < 100 {eV}^{2}$ ,” Phys. Rev. D 86, 052009 (2012); M. G. Aartsen et al. (IceCube Collaboration), “Searches for Sterile Neutrinos with the IceCube Detector,” Phys. Rev. Lett. 117, 071801 (2016); P. Adamson et al. (MINOS+ Collaboration), “Search for sterile neutrinos in MINOS and MINOS+ using a two-detector fit,” arXiv:1710.06488.
G. H. Collin, C. A. Argelles, J. M. Conrad, and M. H. Shaevitz, “Sterile neutrino fits to short baseline data,” arXiv:1602.00671; S. Gariazzo, C. Giunti, M. Laveder, and Y. F. Li, “Updated global 3+1 analysis of short-baseline neutrino oscillations,” arXiv:1703.00860; M. Dentler, A. Hernandez-Cabezudo, J. Kopp, P. A. N. Machado, M. Maltoni, I. Martinez-Soler, and T. Schwetz, “Updated global analysis of neutrino oscillations in the presence of eV-scale sterile neutrinos,” arXiv:1803.10661.
E. Bertuzzo, S. Jana, P. A. N. Machado, and R. Zukanovich Funchal, “A dark neutrino portal to explain MiniBooNE,” arXiv:1807.09877; P. Ballett, S. Pascoli, and M. Ross-Lonergan, “U(1)' mediated decays of heavy sterile neutrinos in MiniBooNE,” arXiv:1808.02915 .
J. R. Jordan, Y. Kahn, G. Krnjaic, M. Moschella, and J. Spitz, “Severe constraints on new physics explanations of the MiniBooNE excess,” arXiv:1810.07185.
M. Ericson, M. V. Garzelli, C. Giunti, and M. Martini, “Assessing the role of nuclear effects in the interpretation of the MiniBooNE low-energy anomaly,” arXiv:1602.01390.

About the Author

Joachim Kopp is a staff scientist at CERN and an Associate Professor for Theoretical Particle Physics at Johannes Gutenberg University Mainz, Germany. He obtained his Ph.D. in 2009 from the University of Heidelberg, working with Manfred Lindner. He then moved to Fermilab as a Research Associate, before returning to Heidelberg as leader of an Otto Hahn Junior Research Group in 2012. He joined Mainz University in 2014 and CERN in 2018. His research is centered around the physics of neutrinos and dark matter, both in laboratory experiments and in the early Universe. For more information about his research, visit http://www.staff.uni-mainz.de/jkopp/