A Multimode Dial for Interatomic Interactions
Interactions mediated by photons are ubiquitous in physical systems. For instance, the van der Waals interaction between atoms in free space—variants of which play a fundamental role in many physical, chemical, and biological processes—is mediated by photons of the electromagnetic vacuum between the atoms. Interestingly, while this interaction is weak and decays with interatomic separation when the atoms are in free space, its strength and range can be modified when the atoms are placed between the mirrors of an optical cavity. When such cavity quantum electrodynamics (QED) systems contain many atoms, they can be used to explore collective quantum phenomena. However, if the atoms dominantly couple to a single cavity light mode, as is usually the case, the photon-mediated interatomic interactions are long-ranged, limiting the phenomena that can be explored. Benjamin Lev from Stanford University, California, and colleagues [1] have now engineered photon-mediated interactions in a cavity QED system that can be tuned from long range to short range. Such tunable-range interactions could be used to study collective quantum phenomena and phase transitions that are currently beyond the reach of other atomic systems and other cavity QED systems.
Lev and co-workers’ study builds on earlier work with cavity QED systems in which a thermal [2] or condensed [3] atomic gas trapped in a cavity is illuminated with a laser beam (the “pump”) orthogonal to the long axis of the cavity (Fig. 1). In these systems, when the pump frequency is far detuned from atomic transitions in the gas and the pump power reaches a certain threshold, the atoms self-organize spontaneously into one of two possible checkerboard patterns while simultaneously “superradiating” light into the cavity. This self-organization transition takes place when the increased kinetic energy of the gas due to a nonuniform density can be compensated by a reduction in the strength of the interatomic interactions mediated by the cavity, which is proportional to the pump power.
Earlier cavity QED studies [3–5] employed high-finesse cavity configurations that allow only one cavity mode to be quasiresonant with the pump. In such “single-mode” cavities, the dominant photon-mediated interactions encompass all of the atoms confined in the volume of the cavity mode, and their strength is modulated with the spatial profile of the quasiresonant mode. Such a global atomic coupling limits the range of observable collective phenomena. It has been known for a while, however, that these cavity QED systems contain, in principle, the basic ingredients that are needed to study rich classes of exotic collective phenomena [6]. Such phenomena have remained inaccessible to ultracold atom setups that employ rigid optical lattices and require interatomic interactions that are spatially strongly fluctuating.
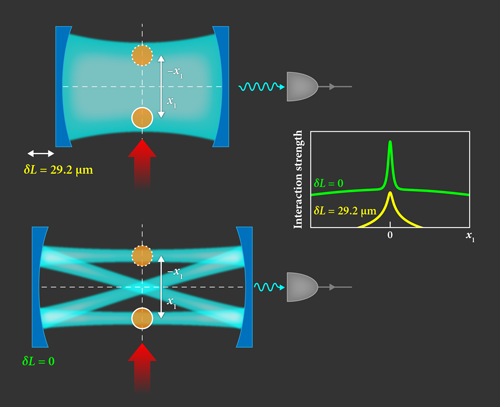
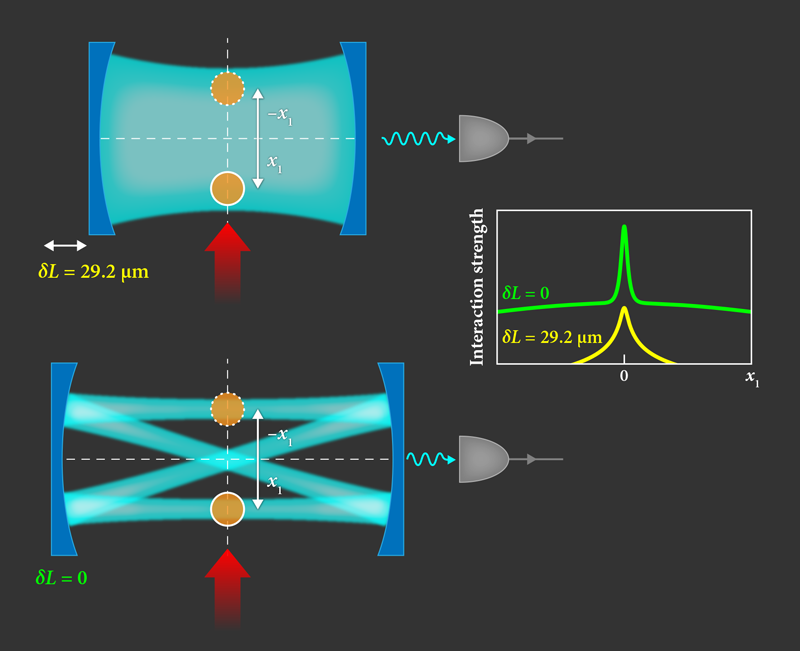
Building on earlier theoretical studies [7], Lev and co-workers have now succeeded in demonstrating tunable-range interactions in these systems. They accomplished this feat using two tricks. The first was to use an adjustable-length cavity that can, with high precision, be brought into a regime where many cavity modes are active. This highly multimode regime is achieved when the separation between the cavity mirrors (the cavity length) is equal to the radius of the mirrors’ curvature. In such a confocal cavity, many modes with different transverse profiles are degenerate (they have the same frequency), and an atom scatters a pump photon into a superposition of the degenerate modes that sensitively depends on the atom’s position. As a result, the photon-mediated interatomic interactions have a much shorter range than in the single-mode case, while remaining much stronger than in free space.
The second trick was to exploit a special symmetry of the confocal configuration to determine the strength of photon-mediated interatomic interactions. In principle, this could be done by measuring the threshold pump power needed for the self-organization transition to take place in two identical point-like atomic condensates placed on the focal plane of the setup and then mapping out its value as a function of the condensates’ separation (Fig. 1). The threshold could be accurately determined from the sharp increase in the number of photons observed at a photodetector placed outside the cavity. A simple relationship between the interaction strength between the condensates and the measured threshold would then be used to calculate the former. However, this approach is prone to two complications: the distortion of the condensates due to collisional interactions between them at small separations, and the unavoidable difference in the size of the condensates. Lev and colleagues circumvented these problems by making use of their theoretical finding that the short-range part of the interaction between two condensates is identical to the short-range part of the interaction between the condensate and its mirror image, which is provided by the confocal cavity. An object located at position on the focal plane of the cavity has a virtual image at (Fig. 1). Armed with these concepts, Lev and colleagues used a single condensate to measure the interaction strength between two condensates. (The authors also performed measurements with two physical condensates, showing that such measurements agree well with the single-condensate data.)
The team finds that when the cavity mirrors are moved away from the confocal configuration, in which only the fundamental transverse mode is quasiresonant with the excited atomic transition [3–5], the interaction strength between the condensate and its mirror image, which is proportional to that between single atoms, decays over a long range; this range is roughly equal to the waist of the Gaussian profile of that mode. When brought towards the confocal configuration, however, the strength decays over a much smaller range—about 10% of the Gaussian waist—demonstrating the tunability of the interactions to a shorter range (Fig. 1).
The authors argue that such tunability opens the door to studying exotic classes of quantum many-body systems such as quantum liquid crystals and strongly correlated materials like high-temperature superconductors [5]. But the most unique aspect of the system studied by Lev and colleagues is probably its potential to provide insights into the poorly understood process of how matter organizes under conditions that are far from thermal equilibrium.
In the authors’ system, a steady flux of energy flows from the pump beam through the condensate to the photodetector outside the cavity, carrying the very signal of the onset of the self-organization transition. Although many of the features of this transition—such as the threshold pump power and the spatial patterns of the superradiance—can be understood through the mean-field theory of equilibrium statistical physics, as demonstrated in this work, it is likely that the quantum fluctuations that drive the transition itself are not described by equilibrium theory. It’s known that equilibrium theory doesn’t adequately describe such fluctuations in the single-mode variant of the transition [8–10]—the same will most likely apply to the multimode-cavity version of the transition. It appears that the nonequilibrium nature of the system, together with its superior controllability [1] and measurability [10] as compared to those of other nonequilibrium systems, will provide a rich basis for investigating new classes of interacting systems.
This research is published in Physical Review X.
References
- V. D. Vaidya et al., “Tunable-Range, Photon-Mediated Atomic Interactions in Multimode Cavity QED,” Phys. Rev. X 8, 011002 (2018).
- A. T. Black, H. W. Chan, and V. Vuletić, “Observation of Collective Friction Forces due to Spatial Self-Organization of Atoms: From Rayleigh to Bragg Scattering,” Phys. Rev. Lett. 91, 203001 (2003).
- K. Baumann, C. Guerlin, F. Brennecke, and T. Esslinger, “Dicke Quantum Phase Transition with a Superfluid Gas in an Optical Cavity,” Nature 464, 1301 (2010).
- K. J. Arnold, M. P. Baden, and M. D. Barrett, “Self-Organization Threshold Scaling for Thermal Atoms Coupled to a Cavity,” Phys. Rev. Lett. 109, 153002 (2012).
- J. Klinder, H. Keßler, M. Wolke, L. Mathey, and A. Hemmerich, “Dynamical Phase Transition in the Open Dicke Model,” Proc. Natl. Acad. Sci. U.S.A. 112, 3290 (2015).
- H. Ritsch, P. Domokos, F. Brennecke, and T. Esslinger, “Cold Atoms in Cavity-Generated Dynamical Optical Potentials,” Rev. Mod. Phys. 85, 553 (2013).
- S. Gopalakrishnan, B. L. Lev, and P. M. Goldbart, “Atom-Light Crystallization of Bose-Einstein Condensates in Multimode Cavities: Nonequilibrium Classical and Quantum Phase Transitions, Emergent Lattices, Supersolidity, and Frustration,” Phys. Rev. A 82, 043612 (2010).
- D. Nagy, G. Szirmai, and P. Domokos, “Critical Exponent of a Quantum Noise-Driven Phase Transition: The Open-System Dicke Model,” Phys. Rev. A 84, 043637 (2011).
- M. Kulkarni, B. Öztop, and H. E. Türeci, “Cavity-Mediated Near-Critical Dissipative Dynamics of a Driven Condensate,” Phys. Rev. Lett. 111, 220408 (2013).
- F. Brennecke, R. Mottl, K. Baumann, R. Landig, T. Donner, and T. Esslinger, “Real-Time Observation of Fluctuations at the Driven-Dissipative Dicke Phase Transition,” Proc. Natl. Acad. Sci. U.S.A. 110, 11763 (2013).