A Magnetic-Field-Free Exciton Condensate
In a semiconductor, an electron can bind to a hole (an empty electronic state with a positive charge) to form a composite particle known as an exciton. Unlike electrons or holes, excitons are bosons. The particles can therefore condense at sufficiently low temperatures into a collective quantum ground state that supports remarkable transport phenomena [1, 2], similar to the zero-resistance flow of current in a superconductor. Thermodynamically stable exciton condensates—condensates that don’t require a constant input of energy—have been produced in certain multilayered structures but only with the application of a large magnetic field, using expensive superconducting magnets. A team led by Emanuel Tutuc at the University of Texas at Austin now reports strong evidence for a similarly stable exciton condensate in a magnetic-field-free setup [3]. Their device consists of a pair of graphene bilayers (two sheets of graphene) separated by an insulating barrier. The long-sought ability to create an exciton condensate without a magnetic field could greatly simplify studies of this many-body effect as well as hasten its use in novel electronic devices.
Making a thermodynamically stable exciton condensate requires a large number of excitons that don’t quickly recombine and produce light. So-called double-layer systems are promising in this pursuit. These devices consist of two thin layers of either semiconducting or semimetallic material that are separated by an insulating barrier. Voltages applied to metallic gates above and below the device create an excess of electrons in one layer and an excess of holes in the other. The Coulomb interaction between electrons and holes is strong enough in these double-layered systems for the particles to form correlated states, while the barrier allows the charge densities in the two layers to be controlled independently.
In principle, a condensate of excitons can form in these systems, provided that the electron-hole correlations are sufficiently strong. But in order to achieve this, other technologically challenging conditions have to be met: The layers have to be relatively free from disruptive impurities and defects; the densities of electrons and holes in the two layers need to be the same; and the distance between electrons and holes in different layers needs to be sufficiently short compared with the distance between electrons (or holes) in the same layer. This latter requirement ensures that correlations between electrons and holes dominate over electron-electron interactions. Researchers have so far succeeded in achieving these conditions and in producing a condensate by using a large magnetic field to drive the electrons and holes into a quantum Hall state [2]. The Landau levels in the quantum Hall regime have a high density of states, which facilitates the formation of exciton states. This in turn permits the use of a relatively wide tunnel barrier, simplifying device fabrication and the control of the relative densities of the layers.
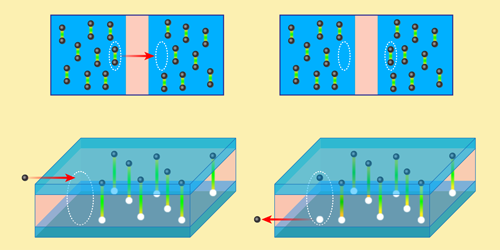
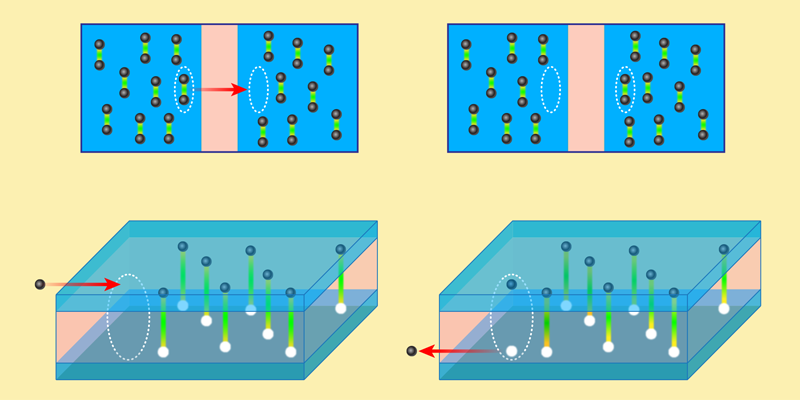
In this previous work with quantum Hall double-layer devices, the evidence for a condensate was primarily based on observations of two predicted features [2, 4–8]. The first of these arises from a gradient in the phase of the condensate order parameter, which produces a current. But since this current corresponds to electrons (in one layer) flowing in the same direction as holes (in the other layer), it is equivalent to electron currents flowing in opposite directions in the two layers—a phenomenon known as dissipationless counterflow. The second experimental feature comes from the fact that excitons can be added to the condensate without changing its energy, since all condensed excitons are in the ground state. Thus, if one applies a tiny bias voltage between the two layers, the conductance of electrons tunneling across the barrier is hugely enhanced compared with when the electrons and holes are uncorrelated [2, 5, 6]. This phenomenon (Fig. 1) is similar to the flow of a supercurrent across a barrier between two superconducting regions (Josephson effect).
In their system of double-bilayer graphene, Tutuc and colleagues observed one of these experimental signatures—Josephson-like tunneling [3]. The device was built from two sheets of bilayer graphene that were separated by two atomic layers of the insulator tungsten diselenide. The researchers used voltage gates on each of the two graphene bilayers to control the electron and hole densities. Thanks to several advances, they were able to obtain a window of densities corresponding to the conditions for an exciton condensate outlined above. These advances include improvements in the design of the tunnel barrier, the preparation of an atomically flat substrate to support the graphene, and methods of aligning the graphene bilayers. Within this optimal density window, and at a low temperature of 1.5 K, they observed a tunneling conductance between the layers at small bias voltage that was many orders of magnitude greater than that predicted for uncorrelated electrons and holes. In fact, the enhancement of the tunneling conductance grew so large that it exceeded the limits of their detectors. In a separate test, the team applied an in-plane magnetic field and confirmed that the tunneling conductance varied with the field strength, similar to what was observed in quantum Hall exciton condensates.
The huge tunneling enhancement observed by Tutuc and colleagues is consistent with the appearance of an exciton condensate. But as with the quantum Hall devices, researchers will expect other experimental observations, such as the dissipationless counterflow, to be convinced that the condensate exists in double-bilayer graphene. Measuring the counterflow may require a different device configuration than Tutuc and colleagues have used here.
These are exciting times for exciton condensate research. In addition to the new work, there has been general experimental progress in observing the condensates in semiconductor quantum wells [9] and in double-bilayer graphene in the quantum Hall regime [10]. The Coulomb interactions between the electrons and holes in double-layer systems can, in principle, be very strong, and it’s conceivable that this feature will allow the creation of condensates at much higher temperatures. These systems could also be the basis for studying topological effects that are thought to exist in exciton condensates [11], like transport phenomena related to topologically protected states confined to the device edges. Now that it might be possible to produce a stable exciton condensate without a magnetic field [3], making electronic devices that rely on the effect would be much simpler. For example, the Josephson-like tunneling conductance is sensitive to temperature, gate voltage, and magnetic field, so one might imagine using these sensitivities to make detectors.
This research is published in Physical Review Letters.
References
- L. V. Keldysh and Yu. V. Kopaev, “Possible Instability of Semimetallic State Toward Coulomb Interaction,” Fiz. Tverd. Tela 6, 2791 (1964), [Sov. Phys. Solid State 6, 2219 (1965)]; Yu. E. Lozovik and V. I. Yudson, “Feasibility of Superfluidity Of Paired Spatially Separated Electrons and Holes; A New Superconductivity Mechanism,” Pis’ma Zh. Eksp. Teor. Fiz. 22, 556 (1975), [JETP Lett. 22, 274 (1975)].
- I. B. Spielman, J. P. Eisenstein, L. N. Pfeiffer, and K. W. West, “Resonantly Enhanced Tunneling in a Double Layer Quantum Hall Ferromagnet,” Phys. Rev. Lett. 84, 5808 (2000); J. P. Eisenstein and A. H. MacDonald, “Bose–Einstein Condensation of Excitons in Bilayer Electron Systems,” Nature 432, 691 (2004).
- G. W. Burg, N. Prasad, K. Kim, T. Taniguchi, K. Watanabe, A. H. MacDonald, L. F. Register, and E. Tutuc, “Strongly Enhanced Tunneling at Total Charge Neutrality in Double-Bilayer Graphene-WSe2 Heterostructures,” Phys. Rev. Lett. 120, 177702 (2018).
- X. G. Wen and A. Zee, “Tunneling in Double-Layered Quantum Hall Systems,” Phys. Rev. B 47, 2265 (1993).
- A. Stern, S. M. Girvin, A. H. MacDonald, and N. Ma, “Theory of Interlayer Tunneling in Bilayer Quantum Hall Ferromagnets,” Phys. Rev. Lett. 86, 1829 (2001).
- T. Hyart and B. Rosenow, “Quantitative Description of Josephson-Like Tunneling in 𝜈T=1 Quantum Hall Bilayers,” Phys. Rev. B 83, 155315 (2011).
- A. D. K. Finck, J. P. Eisenstein, L. N. Pfeiffer, and K. W. West, “Exciton Transport and Andreev Reflection in a Bilayer Quantum Hall System,” Phys. Rev. Lett. 106, 236807 (2011).
- X. Huang, W. Dietsche, M. Hauser, and K. von Klitzing, “Coupling of Josephson Currents in Quantum Hall Bilayers,” Phys. Rev. Lett. 109, 156802 (2012).
- L. Du, X. Li, W. Lou, G. Sullivan, K. Chang, J. Kono, and R.-R. Du, “Evidence for a Topological Excitonic Insulator in InAs/GaSb Bilayers,” Nat. Commun. 8, 1971 (2017).
- J. I. A. Li, T. Taniguchi, K. Watanabe, J. Hone, and C. R. Dean, “Excitonic Superfluid Phase in Double Bilayer Graphene,” Nat. Phys. 13, 751 (2017); X. Liu, K. Watanabe, T. Taniguchi, B. I. Halperin, and P. Kim, “Quantum Hall Drag of Exciton Condensate in Graphene,” Nat. Phys. 13, 746 (2017).
- D. I. Pikulin, P. G. Silvestrov, and T. Hyart, “Confinement-Deconfinement Transition Due to Spontaneous Symmetry Breaking in Quantum Hall Bilayers,” Nat. Commun. 7, 10462 (2016).