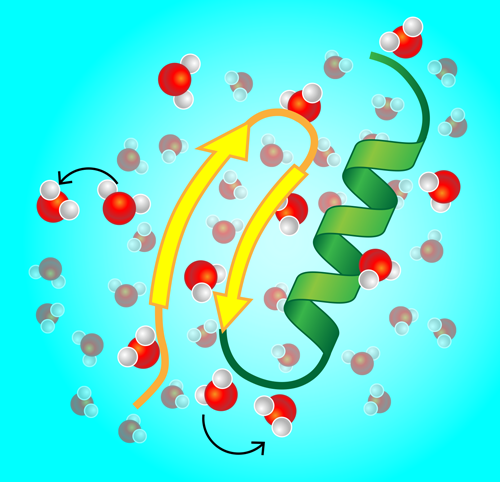
The Dance of Water Molecules around Proteins
Proteins are indispensable molecules in living cells, charged with highly specific tasks ranging from information transmission to metabolism. To perform their duties, proteins need to be in an aqueous solution, which allows them to fold, wrap, and wind. These conformational changes, which are often related to a protein’s functioning, are influenced by the water molecules that surround the solvated protein. But the influence goes both ways since water molecules can be restricted in their movement as they navigate around the complex surface of a protein. A new study of water dynamics around proteins has combined experiments, simulations, and modeling to paint a clear picture of the hopping behavior of surface water molecules [1]. These results might help researchers understand the aging of biopolymer-associated water molecules and the role molecular collisions play in rejuvenating them.
Gone are the days when x-ray images of crystallized proteins stirred much excitement. Instead, ever-more-refined experimental and computational approaches have given us direct glimpses of proteins and other biopolymers in their natural habitat—the wet, crowded environments of living biological cells and membranes. This “wildlife microscopy” has revealed the importance of conformational changes in proteins. For instance, DNA-binding proteins structurally switch between unbound, search, and recognition modes. Similarly, enzymes—the workhorses of cellular metabolism—change shape upon binding and release of a substrate. Given this constant reshaping, one important question is, how does a single protein dynamically couple to its immediate environment, and in particular, to water molecules and ions forming a layer on its surface (Fig. 1)? Experiments that track the dynamics of this so-called hydration water would provide an indirect picture of this coupling.
The study by Liang Hong from Shanghai Jiao Tong University, China, and co-workers is a step in this direction [1]. The researchers present compelling evidence for the anomalous dynamics of surface water around proteins. Using neutron-scattering experiments, Hong and colleagues measured the time it took water molecules to move a certain distance along the surface of two different proteins: cytochrome P450 and green fluorescent protein. They converted this data into a mean-squared displacement, ⟨r2(t)⟩, and showed that the hydration water was subdiffusive in a time window spanning from roughly 10 to 100 picoseconds (ps): In comparison to normal diffusion, where the mean-squared displacement grows linearly with time, the water dynamics along the protein surface is characterized by power-law scaling ⟨r2(t)⟩≃t𝛼, with an anomalous diffusion exponent of 𝛼≈0.8. To examine this subdiffusive behavior over a broader range of timescales, the team performed molecular dynamics (MD) simulations, which showed subdiffusion at short times ( 10 to 103 ps), in agreement with the neutron-scattering experiments. However, at longer times, the simulated water motion became more and more diffusive, with 𝛼 approaching 1 at around 105 ps.
To explain the anomalous dynamics observed in their experiments and simulations, the authors considered a model in which water molecules jump between small cages (or trapping sites) on the surface of the protein. They identified trapping events in their MD simulations and showed that successive jumps were uncorrelated; in other words, the distance and direction of the last jump a water molecule took gives no hint as to what its next jump will be. This result argued against a fractal model of protein surfaces, in which the traps form a highly disordered spatial network. Instead, when the team looked at how long molecules had to wait inside a trap before hopping, they found a broad power-law distribution of waiting times, with lots of shallow (short-wait) traps and very few deep (long-wait) traps. This so-called “scale-free” waiting time distribution is consistent with the continuous-time random walk model [2–4].
A system that exhibits scale-free waiting times is one that is “aging.” Aging in this context means the system is continuously slowing down, as the average waiting time gets longer and longer. This is because more and more molecules become trapped in the rare cages with long waiting times. Previous studies have also reported aging in biopolymer systems. In particular, all-atom molecular dynamics simulations [5] demonstrated subdiffusion and aging for surface water on lipid bilayer membranes with characteristics of both long-tailed waiting time distributions and long-range correlated noise on timescales from 1 ps to 1 𝜇s. Related work presented evidence from simulations that the internal dynamics of proteins is dominated by scale-free waiting times, and thus aging, over several decades in time [6].
Hong and co-workers cement this aging picture with their combination of experiments, simulations, and continuous-time random walk modeling [1]. They also provide an explanation for the observed crossover from subdiffusive to diffusive behavior in their MD simulations. In their model, they assume that only one molecule can occupy a trap at a time. As time goes by, deep traps become filled, forcing water molecules to jump predominantly between shallow traps. These mobile molecules, which are the ones that experiments and simulations focus on, exhibit a nearly normal diffusive behavior. Besides aging, scale-free waiting times in a stochastic process can have other profound consequences [2]. For instance, time-averaged observables such as the mean-squared displacement do not converge to the corresponding ensemble average, even in the long time limit, and thus theoretical results are needed for the proper description of the time averages used to evaluate experiments [2, 3]. This phenomenon gives rise to a significant dynamic heterogeneity: the amplitude of time-averaged observables becomes a random variable for which only the distribution is known [2, 3]. This heterogeneity is evident in experiments that show large variations in measurements of molecular trajectories [2–4, 7, 8]. All these phenomena need to be considered in the interpretation of the observed dynamics and the meaningful extraction of the associated physical parameters, such as mobilities and dynamic scaling exponents.
But even if water dynamics can be simulated up to microsecond scales [1, 6, 7, 9], do these efforts help us understand protein conformational changes that happen over milliseconds? It turns out that they might. First, the results from Hong and co-workers and others teach us that the surface water conformations are more locked than often assumed, and the resulting water dynamics is very inhomogeneous. This may mean that—over long timescales—the water in the protein environment can be treated as two populations: one population of immobile molecules stuck in deep traps and another population of mobile molecules jumping between shallow traps [4]. Second, the protein clock may not tick continuously during a conformational change. Typical cellular liquids are full of large biopolymers incessantly colliding with each other like bumper cars. Collisions with other large biopolymers may “rejuvenate” the protein by releasing locked configurations in the surrounding water. The system may restart with the scale-free dynamics observed at short timescales.
Certainly lots of questions remain open and make this a highly attractive field of study. For instance, how much are proteins and their environments affected by collisions? How many water layers are associated with the protein surface? How is a water molecule replaced once it is kicked out of a surface layer? The search for a better understanding of these questions has essentially just begun, and time will tell how long we will have to wait for answers, with or without a scale.
This research is published in Physical Review Letters.
References
- P. Tan, Y. Liang, Q. Xu, E. Mamontov, J. Li, X. Xing, and L. Hong, “Gradual Crossover from Subdiffusion to Normal Diffusion: A Many-Body Effect in Protein Surface Water,” Phys. Rev. Lett. 120, 248101 (2018).
- R. Metzler, J.-H. Jeon, A. G. Cherstvy, and E. Barkai, “Anomalous Diffusion Models and Their Properties: Non-Stationarity, Non-Ergodicity, and Ageing at the Centenary of Single Particle Tracking,” Phys. Chem. Chem. Phys. 16, 24128 (2014).
- Y. He, S. Burov, R. Metzler, and E. Barkai, “Random Time-Scale Invariant Diffusion and Transport Coefficients,” Phys. Rev. Lett. 101, 058101 (2008).
- J. H. P. Schulz, E. Barkai, and R. Metzler, “Aging Renewal Theory and Application to Random Walks,” Phys. Rev. X 4, 011028 (2014).
- E. Yamamoto, T. Akimoto, M. Yasui, and K. Yasuoka, “Origin of Subdiffusion of Water Molecules on Cell Membrane Surfaces,” Sci. Rep. 4, 4720 (2014).
- X. Hu, L. Hong, M. D. Smith, T. Neusius, X. Cheng, and J. C. Smith, “The Dynamics of Single Protein Molecules is Non-Equilibrium and Self-Similar over Thirteen Decades in Time,” Nat. Phys. 12, 171 (2015).
- K. Nørregaard, R. Metzler, C. M. Ritter, K. Berg-Sørensen, and L. B. Oddershede, “Manipulation and Motion of Organelles and Single Molecules in Living Cells,” Chem. Rev. 117, 4342 (2017).
- S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner, and N. F. Scherer, “Intracellular Transport of Insulin Granules is a Subordinated Random Walk,” Proc. Natl. Acad. Sci. U.S.A. 110, 4911 (2013); A. V. Weigel, B. Simon, M. M. Tamkun, and D. Krapf, “Ergodic and Nonergodic Processes Coexist in the Plasma Membrane as Observed by Single-Molecule Tracking,” Proc. Natl. Acad. Sci. U. S. A. 108, 6438 (2011); J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede, and R. Metzler, “In Vivo Anomalous Diffusion and Weak Ergodicity Breaking of Lipid Granules,” Phys. Rev. Lett. 106, 048103 (2011).
- J.-H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler, and I. Vattulainen, “Protein Crowding in Lipid Bilayers Gives Rise to Non-Gaussian Anomalous Lateral Diffusion of Phospholipids and Proteins,” Phys. Rev. X 6, 021006 (2016).